11
2
Newton's theory of gravitation says that the gravitational force between two point masses is
F=(Gm1m2)/ r2
Where
- G is the gravitational constant: 6.674×10−11 N · (m/kg)2
- m1 is the mass of the first object
- m2 is the mass of the second object
- r is the distance between their centers of mass
Challenge
You need to simulate the pull between two words. Each lowercase letter has mass given by its position in the alphabet. Capital letters have twice the mass of their lowercase counterparts! You will be given a string containing two words separated by several spaces, as well as a positive integer number of seconds, s. Output what the string would look like after s seconds.
Info
- Because words are abstract they have a different set of units and constants
- Mass: WMU (Word Mass Unit) - equal to the mass of the letter 'a'.
- Distance: em, the length of one character.
- Force: NW (Word Newton) = WMU · em/s2
- Gravitational Constant: G = 1 Nw · (em/WMU)2
- The first character corresponds to the position 0 on the x-axis.
- All calculations should be done with as much precision as possible, only at the end do you round to the nearest em.
- You do not need to use calculus, you just need to recalculate the F every second, automatically apply the new acceleration to the velocity, and after a second apply the velocity to the position (see example).
- Once two words collide with each other (like
catdog), they don't move any further.
Center of Mass
The center of mass of a word can be found with the formula:
Where M is the total mass of the word, mi is the mass of a letter, and ri is the position of the letter.
Example:
(Note: Although this example doesn't show it, remember that capital letters have twice the mass of their lowercase counterparts.)
Input: cat dog, 2
First what are the positions of each word? "cat" starts at position 0 and "dog" starts at position 9, so
- xc = 0 and xd = 9
Next, let's find the center of mass of "cat".
- It has a mass of 24 WMU (3+1+20).
- Rc = 1/24(3*0+1*1+20*2) = 41/24 = 1.70833 em
- So unsurprisingly the center of mass is very close to the letter 't'.
Now let's get the center of mass of "dog"
- Rd = 1/26(4*9+15*10+7*11) = 263/26 = 10.11538 em
- So the center of mass for dog is close to the letter 'o', slightly towards 'g'.
Now we can calculate the force between the two words.
- F = 24*26/(10.11538-1.70833)2 = 8.82871 Nw
Now we need to apply this force to both words and get their accelerations
- ac = 8.82871/24 = .36786 em/s2
- ad = -8.82871/26 = -.33957 em/s2
Following the rules above, we apply the acceleration to the velocity, so
- vc = .36786 em/s
- vd = -.33957 em/s
Then we apply the velocity to the position, so after one second,
- xc = .36786 em
- xd = 9 -.33957 = 8.66043 em.
- Rc = 1.70833+.36786 = 2.07619 em
- Rd = 10.11538-.33957 = 9.77581 em
Now we repeat the procedure one more time with the new positions:
- F = 24*26/((9.77581)-(2.07619))2 = 10.52558 Nw
- ac = 10.52558/24 = .43857 em/s2, ad = 10.52558/26 = -.40483 em/s2
- vc = .36786 + .43857 = .80643 em/s, vd = -.33957 - .40483 = -.74440 em/s
- xc = .36786 + .80643 = 1.17429 em, xd = 8.66043 - .74440 = 7.91603 em
- Rc = 2.07619 + .80643 = 2.88262 em, Rd = 9.77581 - .74440 = 9.03141 em
So we end up with "cat" at x=1.17429 and "dog" at x=7.91603.
- We round those to the nearest integer so "cat" goes to position 1 and "dog" goes to position 8, so the output is
cat dog
- We round those to the nearest integer so "cat" goes to position 1 and "dog" goes to position 8, so the output is
Handling Collisions
Remember that the new acceleration is immediately added to the velocity every second. Therefore, if two words collide at certain time, use algebra to find the point of collision. Take this example:
- word 1 is 4 letters long (||w1|| = 4)
- word 2 is 4 letters long (||w2|| = 4)
- x1 = 3, x2 = 8
v1 = 2,v2 = -6
Solve
3 + (4-1) + 2t = 8 - 6t. t = .25s. The position of the collision is xcol = 6.5. Therfore, the collision should appear as occurring between x = 6 and x = 7, as such####@@@@.
The explicit formula for the positions of the words after a collision is
- x1 = floor(xcol)-||w1||+1
- x2 = floor(xcol)+1
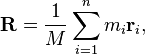
@FryAmTheEggman The last bullet point in "info" talks about collision. You can do it in one step but make sure to follow the rules laid out. – geokavel – 2016-01-14T20:40:31.177
Might the words pass through each other? – xnor – 2016-01-14T21:24:09.510
@xnor No, they're won't. I'm added a part about properly handling collisions. – geokavel – 2016-01-14T21:31:35.827
I'm trying to understand the physics involved here. Consider the configuration
xx a(one space between the wordsxxanda). In Newtonian physics, the force thatafeels would be due to the closerxpulling from a distance of two em's, and the otherxpulling from a distance of three em's, yes? That's not the same as the force of a single point-massXpulling from a distance of2.5em's (i.e., the center of mass of thexx), due to the inverse-square law... – mathmandan – 2016-01-14T22:00:43.9671...so just to clarify, I'm supposed to treat each WORD as if it were a point-mass with all its mass concentrated at its center of mass, where by "its center of mass" we mean "where its center of mass would be if we instead treated its LETTERS as point-masses". Is this correct? – mathmandan – 2016-01-14T22:01:14.167
@mathmandan Yes, I was having that exact question, but I was recommended to do it like this. Your interpretation of the rules is correct. – geokavel – 2016-01-14T22:03:23.160