Finding Exclusive Area in Circle Intersections

Question

Here's a deceptively challenging geometry puzzle for you!

Given a circle A, and n other circles B[n], find the total area contained within A that is not within any circle of B.

Your code should be as short as possible.

Input

Your input should contain the following information:

• A floating-point number to represent the radius of circle A.
• A list of floating-point numbers to represent the radii of circles in B.
• A list of the centers of circles in B. Your program may expect the centers in either polar or Cartesian coordinates.
• Optionally, you may receive the number n of circles in B. This input is not required.

It shall be assumed that the center of circle A is the origin, that is, the point (0, 0).

It is guaranteed that no two circles in B are identical, but it is not guaranteed that: all circles of B intersect A, all centers of B are outside A, or no two circles in B intersect each other. Ensure that your solution can handle various edge cases.

You may receive input in any order, and in the form of text input (through stdin or your language's equivalent), function parameters, or command-line arguments.

If you choose to receive text input, there should be one or two-character printable ASCII delimiters between pieces of input.

Output

Your program or function should output a single floating-point number representing the total area of A not within any of the circles of B. Your answers should be accurate to at least three significant figures for all test cases.

General code-golf rules apply.

Your solution should not rely on sampling points within the circles to determine an area.

Built-ins that automatically locate intersections of circles, find areas within intersections of circles, or solve this problem immediately are disallowed.

Test Cases

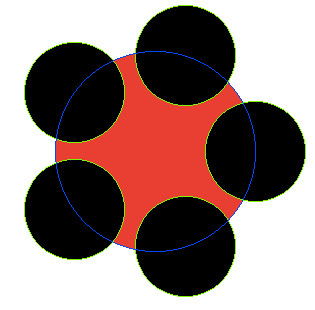
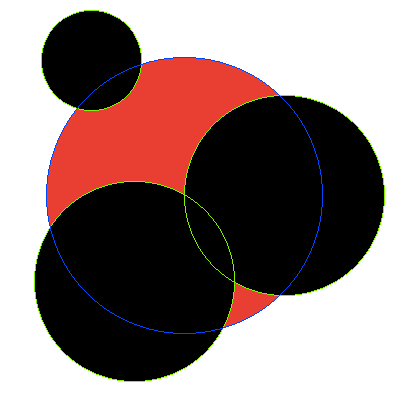
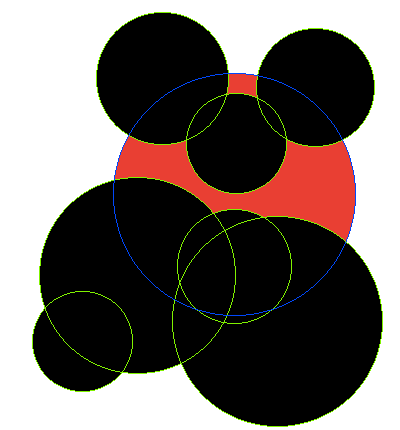
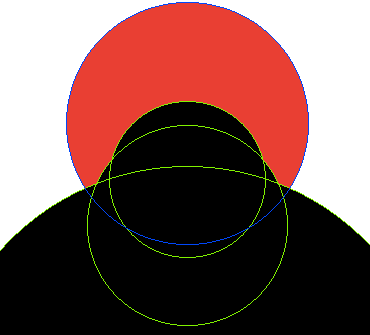
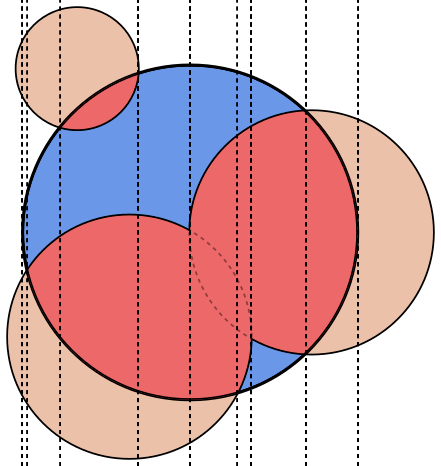
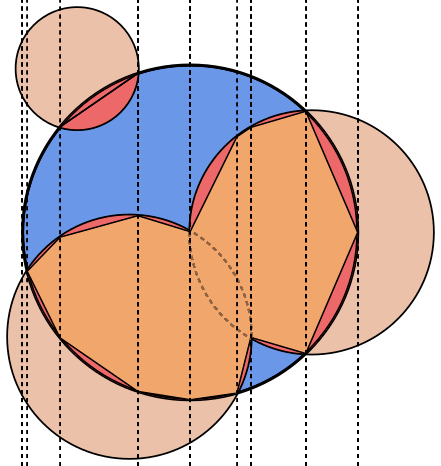
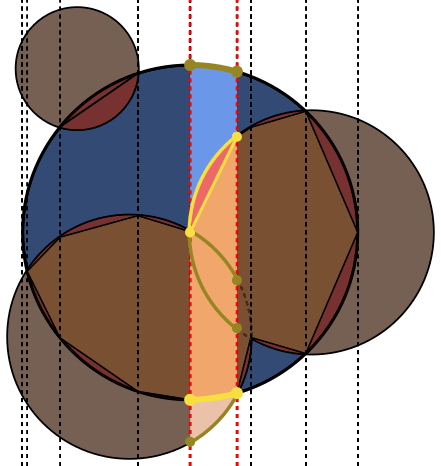
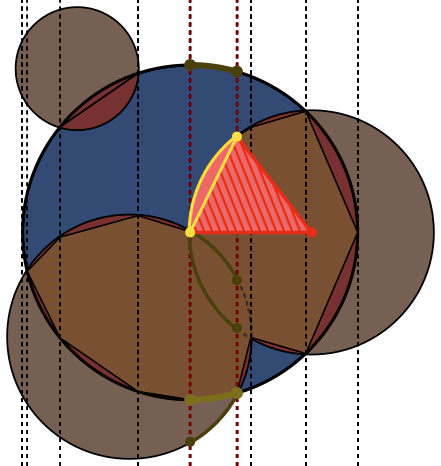
In each image, circle A is outlined in blue, with circles B outlined in green and filled black. The area that should be returned is filled red.

(Special thanks to Rainer P. for checking my solutions)

Test case 1:

A = {x: 0, y: 0, rad: 50}
B[0] = {x: 0, y: 0, rad: 100}

Result: 0.00

Test case 2:

A = {x: 0, y: 0, rad: 100.000000}
B[0] = {x: 100.000000, y: 0.000000, rad: 50.000000}
B[1] = {x: 30.901699, y: -95.105652, rad: 50.000000}
B[2] = {x: -80.901699, y: -58.778525, rad: 50.000000}
B[3] = {x: -80.901699, y: 58.778525, rad: 50.000000}
B[4] = {x: 30.901699, y: 95.105652, rad: 50.000000}

Result: 1.3878e+04

Test case 3:

A = {x: 0, y: 0, rad: 138}
B[0] = {x: 100, y: 0, rad: 100}
B[1] = {x: -50, y: -86, rad: 100} 
B[2] = {x: -93, y: 135, rad: 50}

Result: 1.8969e+04

Test case 4:

A = {x: 0, y: 0, rad: 121.593585}
B[0] = {x: 81.000000, y: 107.000000, rad: 59.841457}
B[1] = {x: -152.000000, y: -147.000000, rad: 50.000000}
B[2] = {x: 43.000000, y: -127.000000, rad: 105.118980}
B[3] = {x: 0.000000, y: -72.000000, rad: 57.870545}
B[4] = {x: -97.000000, y: -81.000000, rad: 98.488578}
B[5] = {x: -72.000000, y: 116.000000, rad: 66.468037}
B[6] = {x: 2.000000, y: 51.000000, rad: 50.000000}

Result: 1.1264e+04

Test case 5:

A = {x: 0, y: 0, rad: 121.605921}
B[0] = {x: 0.000000, y: -293.000000, rad: 250.000000}
B[1] = {x: 0.000000, y: -56.000000, rad: 78.230429}
B[2] = {x: 0.000000, y: -102.000000, rad: 100.000000}

Result: 2.6742e+04

Suggested reading:

Fewell, M. P. "Area of Common Overlap of Three Circles." Oct. 2006. Web. http://dspace.dsto.defence.gov.au/dspace/bitstream/1947/4551/4/DSTO-TN-0722.PR.pdf.

Answer 1

Python 2, 631 bytes

from cmath import*
C=input()
O,R=C[0]
def I(p,r,q,s):
 try:q-=p;d=abs(q*q);x=(r*r-s*s+d)/d/2;return[p+q*(x+z*(r*r/d-x*x)**.5)for z in-1j,1j]
 except:return[]
S=sorted
V=S(i.real for p,r in C for c in C for i in[p-r,p+r]+I(p,r,*c)if-R<=(i-O).real<=R)
A=pi*R*R
for l,r in zip(V,V[1:]):
 H=[]
 for p,t in C:
    try:
     for s in-1,1:a,b=[p.imag+s*(t*t-(p.real-x)**2)**.5for x in l,r];H+=[a+b,a,b,s,t,p],
    except:0
 a,b=H[:2];H=S(H[2:]);n=0;c=a
 for d in H:
    s=d[3];z=.5;H*=d<b
    for q,w,e,_,t,y in(c,min(d,b))*(n-s<(a<d)or[0]*n>H):\
g=phase((l+w*1j-y)/(r+e*1j-y));A-=abs(g-sin(g)).real*t*t/2-z*q*(r-l);z=-z
    n-=s
    if(a<d)*s*n==-1:c=d
print A

^{Line-breaks preceded by \ are for easy reading, and aren't counted in the score.}

Reads input through STDIN as a list of (center, radius) pairs, where center is a complex number in the form X+Yj. The first circle in the list is A (whose center doesn't have to be at the origin), and the rest of the list is B. Prints the result to STDOUT.

Example

Input:  (0+0j, 138),  (100+0j, 100), (-50+-86j, 100), (-93+135j, 50)
Output: 18969.6900901

Explanation

This is a (longer, and much uglier :P) variation on my solution to Martin Büttner's Area of a Self-Intersecting Polygon challenge. It uses the same trick of breaking the problem down into small-enough pieces, for which it becomes more manageable.

We find the points of intersection between all pairs of circles (considering both A, and the circles in B), and pass a vertical line through each of them. Additionally, we pass all the vertical lines tangent to any of the circles. We throw away all the lines that don't intersect A, so that all the remaining lines are between the left and right tangents of A.

We're looking for the area of the intersection of A and the union of the circles in B—the dark red area in the illustration above. This is the area that we have to subtract from A to get the result.

Between each pair of consecutive vertical lines, this area can be broken down into a set of vertical trapezoids (or triangles, or line segments, as special cases of trapezoids), with an "excess" arc segment next to each leg. The fact that we pass as many vertical lines as we do guarantees that the bounded area is indeed no more complicated than that, since otherwise there would have to be an additional point of intersection, and hence an additional vertical line, between the two lines in question.

To find these trapezoids and arc segments, for each pair of consecutive vertical lines, we find the arc segments of each of the circles that properly lie between these two lines (of course, some circles may have no arc segment between a given pair of lines.) In the illustration below, these are the six (bright and dark) yellow arc segments, when considering the two red vertical lines. Note that, since we pass all vertical lines tangent to the circles, if a circle has an arc segment between the two lines, it necessarily intersects both lines, which simplifies the rest of the algorithm.

Not all of these arcs are relevant; we're only interested in the ones that are on the boundary of the intersection between A and the union of B. To find those, we sort the arcs top-to-bottom (note that the arcs may not properly intersect each other, since this would imply the existence of another vertical line between the two we're considering, and so it makes sense to talk about an arbitrary arc being above, or below, any other one.)

We traverse the arcs, in order, while keeping count of the number of B circles we're currently inside, n. If n changes from 0 to 1 while we're inside A, or if we're at the top arc of A while n is nonzero, then the current arc corresponds to one leg of a trapezoid. If n changes from 1 to 0 while we're inside A, or if we're at the bottom arc of A while n is nonzero, then the current arc corresponds to the other leg of the same trapezoid. Once we find such a pair of arcs (the two bright yellow arcs in the above illustration), we calculate the area of the corresponding trapezoid, and of the two arc segments, and add it to the total area to be subtracted from A.

Calculating the area of A, as well as the areas of the trapezoids, is fairly straight forward. The area of each arc segment is the area of the corresponding circular sector, minus the area of the triangle whose vertices are the two endpoints of the arc segment, and the center of the corresponding circle.