Draw the Pentaflake

Question

First of all ... I would like to wish everyone a Merry Christmas (sorry if I am a day late for your timezone).

To celebrate the occasion, we are going to draw a snowflake. Because the year is 2015 and Christmas is on the 25th (for a large portion of persons), we will draw a Pentaflake. The Pentaflake is a simple fractal composed of pentagons. Here are a few examples (taken from here):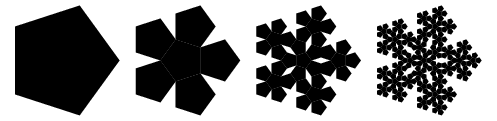

Each Pentaflake has an order n. The Pentaflake of order 0 is simply a pentagon. For all other orders n, a Pentaflake is composed of 5 Pentaflakes of the previous order arranged around a 6th Pentaflake of the previous order. For example, a Pentaflake of order 1 is composed of 5 pentagons arranged around a central pentagon.

Input

The order n. This may be given in any way except that of a predefined variable.

Output

An image of the order n Pentaflake. Must be at least 100px wide and 100px long. It may be saved to a file, displayed to the user, or outputted to STDOUT. Any other form of output is not allowed. All image formats existing before this challenge are allowed.

Winning

As codegolf, the person with the least number of bytes wins.

Answer 1

Matlab, 226

function P(M);function c(L,X,Y,O);hold on;F=.5+5^.5/2;a=2*pi*(1:5)/5;b=a(1)/2;C=F^(2*L);x=cos(a+O*b)/C;y=sin(a+O*b)/C;if L<M;c(L+1,X,Y,~O);for k=1:5;c(L+1,X+x(k),Y+y(k),O);end;else;fill(X+x*F, Y+y*F,'k');end;end;c(0,0,0,0);end

Ungolfed:

function P(M);                
function c(L,X,Y,O);          %recursive function
hold on;
F=.5+5^.5/2;                  %golden ratio
a=2*pi*(1:5)/5;               %full circle divided in 5 parts (angles)
b=a(1)/2;
C=F^(2*L);
x=cos(a+O*b)/C;               %calculate the relative position ofnext iteration
y=sin(a+O*b)/C;
if L<M;                       %current recursion (L) < Maximum (M)? recurse
    c(L+1,X,Y,~O);            %call recursion for inner pentagon
    for k=1:5;
        c(L+1,X+x(k),Y+y(k),O)%call recursion for the outer pentagons
    end; 
else;                         %draw
    fill(X+x*F, Y+y*F,'k');  
end;
end;
c(0,0,0,0);
end

Fifth iteration (already took quite a while to render).

A slight alteration of the code (unfortunately more bytes) results in this beauty=)

Oh, and another one:

Answer 2

Mathematica, 200 bytes

a=RotationTransform
b=Range
r@k_:={Re[t=I^(4k/5)],Im@t}
R@k_:=a[Pi,(r@k+r[k+1])/2]
Graphics@Nest[GeometricTransformation[#,ScalingTransform[{1,1}(Sqrt@5-3)/2]@*#&/@Append[R/@b@5,a@0]]&,Polygon[r/@b@5],#]&

The last line is a function which can be applied to an integer n.

Mathematica function names are long. Somebody should entropy-encode them and make a new language from it. :)

When applied to 1:

When applied to 2:

Answer 3

MATLAB, 235 233 217 bytes

Update: a bunch of suggestions from @flawr helped me lose 16 bytes. Since only this allowed me to beat flawr's solution, and that I wouldn't have found the challenge without flawr's help in the first place, consider this a joint submission by us:)

N=input('');f=2*pi/5;c=1.5+5^.5/2;g=0:f:6;p=[cos(g);sin(g)];R=[p(:,2),[-p(2,2);p(1,2)]];for n=1:N,t=p;q=[];for l=0:4,q=[q R^l*[c-1+t(1,:);t(2,:)]/c];end,p=[q -t/c];end,p=reshape(p',5,[],2);fill(p(:,:,1),p(:,:,2),'k');

This is another MATLAB solution, this one based on a philosophy of iterated function systems. I was mostly interested in developing the algorithm itself, and I haven't golfed too much on the solution. There's surely room for improvement. (I contemplated using a hard-coded fixed-point approximation for c, but that wouldn't be nice.)

Ungolfed version:

N=input('');                                % read order from stdin

f=2*pi/5;                                   % angle of 5-fold rotation
c=1.5+5^.5/2;                               % scaling factor for contraction

g=0:f:6;
p=[cos(g);sin(g)];                          % starting pentagon, outer radius 1
R=[p(:,2),[-p(2,2);p(1,2)]];                % 2d rotation matrix with angle f

for n=1:N,                                  % iterate the points
    t=p;
    q=[];
    for l=0:4,
       q=[q R^l*[c-1+t(1,:);t(2,:)]/c];     % add contracted-rotated points
    end,
    p=[q -t/c];                             % add contracted middle block
end,

p=reshape(p',5,[],2);                 % reshape to 5x[]x2 matrix to separate pentagons
fill(p(:,:,1),p(:,:,2),'k');          % plot pentagons

Result for N=5 (with a subsequent axis equal off for prettiness, but I hope that doesn't count byte-wise):

Answer 4

Mathematica, 124 bytes

Mathematica supports new syntax for Table since version 10: Table[expr, n], which saves another byte. Table[expr, n] is equivalent to Table[expr, {n}].

f@n_:=(p=E^Array[π.4I#&,5];Graphics@Map[Polygon,ReIm@Fold[{g,s}~Function~Join[.62(.62g#+#&/@s),{-.39g}],p,p~Table~n],{-3}])

The core of this function is using complex numbers to do tranformations and then convert them to points by ReIm.

Test case:

f[4]

Answer 5

Mathematica, 199 196 bytes

Edging out Peter Richter's answer by a hair, here's one of my own. It leans heavily on graphics functionality, and less on math and FP. The CirclePoints builtin is new in 10.1.

c=CirclePoints;g=GeometricTransformation;
p@0=Polygon@c[{1,0},5];
p@n_:=GraphicsGroup@{
        p[n-1],
        g[
          p[n-1]~g~RotationTransform[Pi/5],
          TranslationTransform/@{GoldenRatio^(2n-1),n*Pi/5}~c~5
        ]
      };
f=Graphics@*p

Edit: Thanks to DumpsterDoofus for GoldenRatio

Answer 6

Mathematica, 130 bytes

r=Exp[Pi.4I Range@5]
p=1/GoldenRatio
f@0={r}
f@n_:=Join@@Outer[1##&,r,p(f[n-1]p+1),1]~Join~{-f[n-1]p^2}
Graphics@*Polygon@*ReIm@*f

I use a similar technique to njpipeorgan's answer (in fact I stole his 2Pi I/5 == Pi.4I trick), but implemented as a recursive function.

Example usage (using % to access the anonymous function that was output on the last line):

 %[5]