Draw a Christmas Star / Stellated Dodecahedron

Question

Paper stars are a big thing in my family at christmas, so I thought a virtual one would be cool.

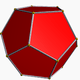
Below is an image of a regular dodecahedron (from https://en.wikipedia.org/wiki/Dodecahedron, attributed to the author mentioned there.)

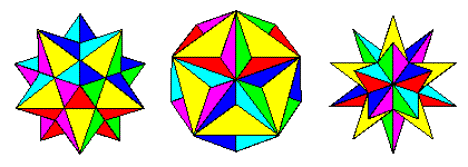
The process of stellation (wikipedia) when applied to a polyhedron involves extending the faces until they cross other faces. Thus starting with the regular dodecahedron, we obtain the following shapes:

Small Stellated Dodecahedron, Great Dodecahedron and Great Stellated Dodecahedron

Image from http://jwilson.coe.uga.edu/emat6680fa07/thrash/asn1/stellations.html

These are the three possible Stellations of the dodecahedron (Wolfram). They form a natural progression from the dodecahedron, to the small stellated dodecahedron, great dodecahedron and great stellated dodecahedron, as we extend the faces further and further out.

Task

Your program or function should display or output to an image file one of the following polyhedra: Regular dodecahedron, Small stellated dodecahedron, Great dodecahedron or Great Stellated Dodecahedron.

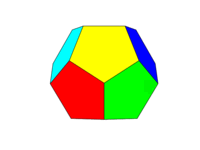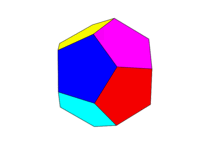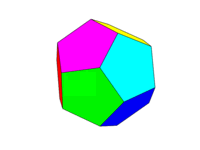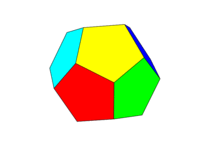
The colour scheme should be as the second image above. Each of the six pairs of opposite faces shall be one of the six colours Red, Yellow, Green, Cyan, Blue, and Magenta. You may use default colours with these names in your language or its documentation, or use the colours FF0000, FFFF00, 00FF00, 00FFFF, 0000FF, and FF00FF (you may tone these down by reducing the intensity to a minimum of 75% if desired, for example by reducing the F's to C's.)

Note that we define a "face" as being all areas in the same plane. Thus in the images above the front face is yellow (and the parallel back face would also be yellow.)

Background should be black, grey, or white. Edges may be omitted, but should be black if drawn.

Rules

The displayed polyhedron must be between 500 and 1000 pixels in width (width is defined as the maximum distance between any two displayed vertices.)

The displayed polyhedron must be in perspective projection (viewpoint at least 5 widths away from the polyhedron), or orthographic projection (effectively a perspective projection with the viewpoint at infinity).

The polyhedron must be displayable from any angle. (It is not acceptable to pick the easiest possible angle and making a hardcoded 2D shape.) The angle can be specified by the user in either of the following ways:

1. Input of three angles corresponding to three rotations, from stdin, or as function or commandline parameters. These can be either Euler angles (where the first and last rotations are about the same axis) or Tait-Bryan angles (where there is one rotation each about the x, y and z axis) https://en.wikipedia.org/wiki/Euler_angles (simply put, anything goes so long as each rotation is about the x, y, or z axis and consecutive rotations are about perpendicular axes.)

2. Facility for the user to rotate the polyhedron in steps of not more than 10 degrees about the x and y axes and refresh the display, any arbitrary number of times (assuming z axis perpendicular to the screen).

The polyhedron must be solid, not wireframe.

No builtins for drawing polyhedra are allowed (I'm looking at you, Mathematica!)

Scoring

This is codegolf. Shortest code in bytes wins.

Bonuses

Multiply your score by 0.5 if you do not use builtins for 3D drawing.

Multiply your score by 0.7 if you can display all three of the stellations of the dodecahedron, selectable by the user by an integer 1-3 entered from stdin, or by function or commandline parameter.

If you go for both bonuses your score will be multiplied by 0.5*0.7=0.35

Useful info (sources as below)

https://en.wikipedia.org/wiki/Regular_dodecahedron

https://en.wikipedia.org/wiki/Regular_icosahedron

The dodecahedron has 20 vertices. 8 of them form the vertices of a cube with the following cartesian (x,y,z) coordinates:

(±1, ±1, ±1)

The remaining 12 are as follows (phi is the golden ratio)

(0, ± 1 / φ , ±φ)

(± 1 / φ , ±φ, 0)

(±φ, 0, ± 1 / φ )

The convex hull of the small stellated dodecahedron and great dodecahedron is obviously a regular dodecahedron. The outer vertices describe an icosahedron.

According to Wikipedia an icosahedron's 12 vertices can be described in a similar manner as cyclic permutations of (0, ±1, ±φ). The outer vertices of the small stellated dodecaheron and great dodechahedron (on the same scale as the dodecahedron above) form a larger icosahedron, where the coordinates of the vertices are cyclic permutations of (0, ±φ^2, ±φ).

The angles between faces for the dodecahedron and icosahedron are 2 arctan(phi) and arccos(-(√5)/3) respectively.

For tips on rotating, see https://en.wikipedia.org/wiki/Rotation_matrix

EDIT: By mistake I have allowed the regular dodecahedron, and can't retract it now. The x0.7 bonus for drawing all three of the stellated polyhedra remains. On New Year's Day I will issue a bounty of 100 for the answer that can display the most of the four polyhedra, with shortest code as the tie break.

Answer 1

Mathematica, 426 424 bytes

Graphics3D[{Red,Yellow,Green,Cyan,Blue,Magenta}~Riffle~(a=Partition)[Polygon/@Uncompress@"1:eJxtkjEKwkAURNeoySYgeAVP4QFsrcTGTiyUBcEith7A2wgKgpVH8/vgs2TYZmAyw9/5k784XDbHVwihnxisU39N9SiEdI8GO/uWHpXBtjFAgJ7HToFl5WabEdJ+anCqDb6dU9RP65NR59EnI0CZDAWYjFmomBmPCn3/hVVwc9s4xYd66wYqFJVvhMz75vWlHIkhG2HBDJ1V3kYps7z7jG6GomIu/QUJKTGkdtlX2pDM8m6pydyzHIOElBhyG6V9cxulzPldaVJ6lpuUkKUTzWcm+0obkrn0f3OT0rMc0jDkD37nlUo="~a~3~a~5,2],Boxed->1<0]

Uses the built-in Graphics3D to display the shape. Most of the bytes are taken up by the compressed vertex locations, however, which are then Partitioned into a form usable by Polygon. Finally:

Note that this shape can be rotated by clicking and dragging.

Answer 2

Python 2.7, 949 bytes

Here is the solution for the regular dodecahedron plotted using matplotlib. The rough outline for the ungolfed code (not shown here) was is outlined below:

• Make vertices Make edges (based on 3 nearest neighbours, module scipy.spatial.KDtree)
• Make faces based on graph cycles with length 5 (module networkx)
• Make facenormals (and select those with outward facing normal, numpy.cross)
• Generate coloring based on face normals
• Plotting using matplotlib

import itertools as it
import numpy as np
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import matplotlib.pyplot as plt
v=[p for p in it.product((-1,1),(-1,1),(-1,1))]
g=.5+.5*5**.5
v.extend([p for p in it.product((0,),(-1/g,1/g),(-g,g))])
v.extend([p for p in it.product((-1/g,1/g),(-g,g),(0,))])
v.extend([p for p in it.product((-g,g),(0,),(-1/g,1/g))])
v=np.array(v)
g=[[12,14,5,9,1],[12,1,17,16,0],[12,0,8,4,14],[4,18,19,5,14],[4,8,10,6,18],[5,19,7,11,9],[7,15,13,3,11],[7,19,18,6,15],[6,10,2,13,15],[13,2,16,17,3],[3,17,1,9,11],[16,2,10,8,0]]
a=[2,1,0,3,4,5,0,1,2,3,4,5]
fig = plt.figure()
ax = fig.add_subplot((111),aspect='equal',projection='3d')
ax.set_xlim3d(-2, 2)
ax.set_ylim3d(-2, 2)
ax.set_zlim3d(-2, 2)
for f in range(12):
 c=Poly3DCollection([[tuple(y) for y in v[g[f],:]]], linewidths=1, alpha=1)
 c.set_facecolor([(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0)][a[f]])
 ax.add_collection3d(c)
ax.auto_scale_xyz
plt.show()

Answer 3

Ruby, 784 bytes * 0.5 * 0.7 = 274.4

My own answer, therefore not eligible for my bounty.

Eligible for both the non-3D builtin bonus and the drawing all stellations bonus.

->t,n{o=[]
g=->a{a.reduce(:+)/5}
f=->u,v,w,m{x=u.dup;y=v.dup;z=w.dup
15.times{|i|k,l=("i".to_c**(n[i/5]/90.0)).rect
j=i%5
x[j],y[j],z[j]=y[j],x[j]*k+z[j]*l,z[j]*k-x[j]*l}
p=g[x];q=g[y];r=g[z]
a=[0,1,-i=0.382,-1][t]*e=r<=>0
b=[j=1+i,0,j,j][t]*e
c=[-i*j,-i,1,i][t]*e
d=[j*j,j,0,0][t]*e
5.times{|i|o<<"<path id=\"#{"%9.0f"%(z[i]*a+r*b+(z[i-2]+z[i-3])*c+2*r*d+999)}\"
d=\"M#{(x[i]*a+p*b)} #{(y[i]*a+q*b)}L#{(x[i-2]*c+p*d)} #{(y[i-2]*c+q*d)}L#{(x[i-3]*c+p*d)} #{(y[i-3]*c+q*d)}\"
fill=\"##{m}\"/>"}}
a=233
b=377
z=[0,a,b,a,0]
y=[a,b,0,-b,-a]
x=[b,0,-a,0,b]
w=[-b,0,a,0,-b]
f[x,y,z,'F0F']
f[w,y,z,'0F0']
f[y,z,x,'00F']
f[y,z,w,'FF0']
f[z,x,y,'F00']
f[z,w,y,'0FF']
s=File.open("p.svg","w")
s.puts'<svg xmlns="http://www.w3.org/2000/svg" viewBox="-450 -450 900 900">',o.sort,'</svg>'
s.close}

Input as function parameters

An integer 0..3 corresponding to regular dodecahedron, small stellated dodecahedron, great stellated dodecahedron

An array of three integers corresponding to degree angles for rotations about the x, y and x (again) axes (proper Euler angles, enabling any rotation to be achieved.)

Output a file p.svg that can be displayed in a web browser.

Explanation

the arrays x,y,z at the bottom of the code contain the coordinates of the outer points of one face of a small stellated dodecahedron. This can be inscribed in the icosahedron whose 12 vertices are defined by the cyclic permutations of (+/-377,+/-233,+/-0). Note that 377 and 233 are consecutive Fibonacci numbers and therefore 377/233 is an excellent approximation to the golden ratio.

an additional array w contains the x coordinates multiplied by -1, equivalent to reflection in the x plane. Function f is called 6 times, once for each colour, with the different cyclic permutations of x,y,z and w,y,z.

The three rotations are passed as parameters in n[]. to use sin and cos in Ruby, it is necessary to do include Math. to avoid this, the cosine and sine of the angle are obtained by raising the square root of -1 "i" to a power of (angle in degrees / 90) The real and imaginary parts of this number are stored in k (cosine) and l (sine)

Prior to rotation, x and y values are exchanged. Then matrix multiplication is applied to the y and z values to give a rotation about the x axis. The exchanging of values enables the three rotations to be carried out in a loop.

So far, we only have one ring of points. To obtain the rest, we need to find the centre of the pentagon/star. This is done by finding the average of coordinates of the 5 vertices, which are stored in p,q,r.

As mentioned before, only one function call per colour is made. The sign of r (the average of the z coordinates, and therefore the coordinate of the face) is tested. If it is positive, the face is a front face and therefore visible. If it is negative, the face is a back face. It is invisible, and we have no function call for the opposite face. Therefore, all three coordinates must be inverted. The sign of r is stored in e to facilitate this.

The face is constructed of 5 triangles, whose vertices are linear combinations of the outer vertices of the small stellated dodecahedron and the centre of the face. In the case of the small stellated dodecahedron, for the tips of the triangles we set a=1 and b=0 (contribution 1 from x,y,z and 0 from p,q,r). For the 2 base vertices of the triangle we set c=-0.382 (contribution 1/golden ratio^2 from x,y,z) and d=1.382 (contribution from p,q,r.) The reason for the negative contribution is that the base vertices of the triangle are defined in terms of the opposing tips, which are on the opposite side of the face. The obtained coordinates are multiplied by e as necessary.

The four unnamed arrays whose values are assigned to a,b,c,d contain the required values for the regular dodecahedron, small stellated dodecahedron, great dodecahedron and great stellated dodecahedron, selected according to variable t Note that for the small stellated dodecahedron and great dodecahedron, a+b=c+d=1. The relation a+b=c+d applies to the other shapes, but a different scale is applied.

A line of svg code is created for each triangle. This contains an ID derived from the sum of the z coordinates of the 3 vertices of the triangle, a description of the vertices of the three coordinates of the triangle, and a colour. note that we view straight down the z axis in orthographic projection. Thus 2D x = 3D x and 2D y = 3D y. The line is added to h.

finally, after all the function calls are finished, h is sorted so that the triangles of highest z value (in front) are plotted last, and the whole thing is saved as an svg file with the appropriate header and footer text.

Ungolfed in test program

h=->t,n{                                              #t=type of polygon,n=angles of rotation
o=[]                                                  #array for output
g=->a{a.reduce(:+)/5}                                 #auxiliary function for finding average of 5 points

f=->u,v,w,m{x=u.dup;y=v.dup;z=w.dup                   #function to take 5 points u,v,w and plot one face (5 triangles) of the output in colour m 

  15.times{|i|                                        #for each of 3 rotation angle and 5 points
    k,l=("i".to_c**(n[i/5]/90.0)).rect                #calculate the cos and sine of the angle, by raising sqrt(-1)="i" to a power
    j=i%5                                             #for each of the 5 points
    x[j],y[j],z[j]=y[j],x[j]*k+z[j]*l,z[j]*k-x[j]*l}  #swap x and y, then perform maxtrix rotation on (new) y and z.

  p=g[x];q=g[y];r=g[z]                                #find centre p,q,r of the face whose 5 points (in the case of small stellated dodecahedron) are in x,y,z

  e=r<=>0                                             #if r is positive, face is front. if negative, face is back, so we need to transform it to opposite face.
  a=[0,              1,    -0.382,    -1][t]*e        #contribution of 5 points x,y,z to triangle tip vertex coordinates
  b=[1.382,          0,     1.382,     1.382][t]*e    #contribution of centre p,q,r to triangle tip vertex coordinates
  c=[-0.528,        -0.382, 1,         0.382][t]*e    #contribution of 5 points x,y,z to coordinates of each triangle base vertex 
  d=[1.901,          1.382, 0,         0][t]*e        #contribution of centre p,q,r to coordinates of each triangle base vertex

  5.times{|i|
  o<<"<path id=\"#{"%9.0f"%(z[i]*a+r*b+(z[i-2]+z[i-3])*c+2*r*d+999)}\"
d=\"M#{(x[i]*a+p*b)} #{(y[i]*a+q*b)}L#{(x[i-2]*c+p*d)} #{(y[i-2]*c+q*d)}L#{(x[i-3]*c+p*d)} #{(y[i-3]*c+q*d)}\"
fill=\"##{m}\"/>"}                                    #write svg code for this triangle 
}

  a=233                                               #a,b =coordinate standard values 
  b=377
  z=[0,a,b,a,0]                                       #z coordinates for one face of stellated dodecahedron 
  y=[a,b,0,-b,-a]                                     #y coordinates
  x=[b,0,-a,0,b]                                      #x coordinates
  w=[-b,0,a,0,-b]                                     #alternate  x coordinates

  f[x,y,z,'F0F']                                      #call f
  f[w,y,z,'0F0']                                      #to plot
  f[y,z,x,'00F']                                      #each
  f[y,z,w,'FF0']                                      #face
  f[z,x,y,'F00']                                      #in
  f[z,w,y,'0FF']                                      #turn

  s=File.open("p.svg","w")                            #sort output in o, plot front triangles last
  s.puts'<svg xmlns="http://www.w3.org/2000/svg" viewBox="-450 -450 900 900">',o.sort,'</svg>'
  s.close                                             #add header and footer, and save as svg
}

t=gets.to_i
n=[]
3.times{n<<gets.to_i}
h[t,n]

Output

for small stellated dodecahedron (will add some images of the other polygons soon)

1,0,0,0 home position

1,30,0,0 rotate down 30 degrees

1,0,30,0 rotate right 30 degrees (note: for a perfect side view, the rotation would be atan(1/golden ratio)=31.7 degrees, hence we can still see a small sliver of blue)

1,0,20,0 rotate right 20 degrees

1,60,10,-63 rotate down, right and up (example of orientation only possible with 3 rotations)

0,30,0,0 regular dodecahedron

2,0,20,0 great dodecahedron

3,45,45,45 great stellated dodecahedron