Which finite abelian group is this?

Question

Description

Write a function f(m, G) that accepts as its arguments a mapping m, and a set/list of distinct, non-negative integers G.

m should map pairs of integers in G to new integers in G. (G, m) is guaranteed to form a finite abelian group, but any element of G may be the identity.

There is an important theorem that says:

[Each finite abelian group] is isomorphic to a direct product of cyclic groups of prime power order.

f must return a list of prime powers [p1, ... pn] in ascending order such that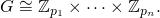

Examples

• f((a, b) → (a+b) mod 4, [0, 1, 2, 3]) should return [4], as the parameters describe the group Z₄.

• f((a, b) → a xor b, [0, 1, 2, 3]) should return [2, 2], as the parameters describe a group isomorphic to Z₂ × Z₂.

• f((a, b) → a, [9]) should return [], as the parameters describe the trivial group; i.e., the product of zero cyclic groups.

• Define m as follows:

  (a, b) → (a mod 3 + b mod 3) mod 3
         + ((floor(a / 3) + floor(b / 3)) mod 3) * 3
         + ((floor(a / 9) + floor(b / 9)) mod 9) * 9
  

  Then f(m, [0, 1, ..., 80]) should return [3, 3, 9], as this group is isomorphic to Z₃ × Z₃ × Z₉

Rules

• m may either be a function (or function pointer to some function) Int × Int → Int, or a dictionary mapping pairs in G × G to new elements of G.

• f may take its parameters in the opposite order, i.e. you may also implement f(G, m).

• Your implementation should theoretically work for arbitrarily large inputs, but need not actually be efficient.

• There is no limitation on using built-ins of any kind.

• Standard code-golf rules apply. Shortest code in bytes wins.

Leaderboard

For your score to appear on the board, it should be in this format:

# Language, Bytes

var QUESTION_ID=67252,OVERRIDE_USER=3852;function answersUrl(e){return"http://api.stackexchange.com/2.2/questions/"+QUESTION_ID+"/answers?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+ANSWER_FILTER}function commentUrl(e,s){return"http://api.stackexchange.com/2.2/answers/"+s.join(";")+"/comments?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+COMMENT_FILTER}function getAnswers(){jQuery.ajax({url:answersUrl(answer_page++),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){answers.push.apply(answers,e.items),answers_hash=[],answer_ids=[],e.items.forEach(function(e){e.comments=[];var s=+e.share_link.match(/\d+/);answer_ids.push(s),answers_hash[s]=e}),e.has_more||(more_answers=!1),comment_page=1,getComments()}})}function getComments(){jQuery.ajax({url:commentUrl(comment_page++,answer_ids),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){e.items.forEach(function(e){e.owner.user_id===OVERRIDE_USER&&answers_hash[e.post_id].comments.push(e)}),e.has_more?getComments():more_answers?getAnswers():process()}})}function getAuthorName(e){return e.owner.display_name}function process(){var e=[];answers.forEach(function(s){var r=s.body;s.comments.forEach(function(e){OVERRIDE_REG.test(e.body)&&(r="<h1>"+e.body.replace(OVERRIDE_REG,"")+"</h1>")});var a=r.match(SCORE_REG);a&&e.push({user:getAuthorName(s),size:+a[2],language:a[1],link:s.share_link})}),e.sort(function(e,s){var r=e.size,a=s.size;return r-a});var s={},r=1,a=null,n=1;e.forEach(function(e){e.size!=a&&(n=r),a=e.size,++r;var t=jQuery("#answer-template").html();t=t.replace("{{PLACE}}",n+".").replace("{{NAME}}",e.user).replace("{{LANGUAGE}}",e.language).replace("{{SIZE}}",e.size).replace("{{LINK}}",e.link),t=jQuery(t),jQuery("#answers").append(t);var o=e.language;/<a/.test(o)&&(o=jQuery(o).text()),s[o]=s[o]||{lang:e.language,user:e.user,size:e.size,link:e.link}});var t=[];for(var o in s)s.hasOwnProperty(o)&&t.push(s[o]);t.sort(function(e,s){return e.lang>s.lang?1:e.lang<s.lang?-1:0});for(var c=0;c<t.length;++c){var i=jQuery("#language-template").html(),o=t[c];i=i.replace("{{LANGUAGE}}",o.lang).replace("{{NAME}}",o.user).replace("{{SIZE}}",o.size).replace("{{LINK}}",o.link),i=jQuery(i),jQuery("#languages").append(i)}}var ANSWER_FILTER="!t)IWYnsLAZle2tQ3KqrVveCRJfxcRLe",COMMENT_FILTER="!)Q2B_A2kjfAiU78X(md6BoYk",answers=[],answers_hash,answer_ids,answer_page=1,more_answers=!0,comment_page;getAnswers();var SCORE_REG=/<h\d>\s*([^\n,]*[^\s,]),.*?(\d+)(?=[^\n\d<>]*(?:<(?:s>[^\n<>]*<\/s>|[^\n<>]+>)[^\n\d<>]*)*<\/h\d>)/,OVERRIDE_REG=/^Override\s*header:\s*/i;

body{text-align:left!important}#answer-list,#language-list{padding:10px;width:290px;float:left}table thead{font-weight:700}table td{padding:5px}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script> <link rel="stylesheet" type="text/css" href="//cdn.sstatic.net/codegolf/all.css?v=83c949450c8b"> <div id="answer-list"> <h2>Leaderboard</h2> <table class="answer-list"> <thead> <tr><td></td><td>Author</td><td>Language</td><td>Size</td></tr></thead> <tbody id="answers"> </tbody> </table> </div><div id="language-list"> <h2>Winners by Language</h2> <table class="language-list"> <thead> <tr><td>Language</td><td>User</td><td>Score</td></tr></thead> <tbody id="languages"> </tbody> </table> </div><table style="display: none"> <tbody id="answer-template"> <tr><td>{{PLACE}}</td><td>{{NAME}}</td><td>{{LANGUAGE}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody> </table> <table style="display: none"> <tbody id="language-template"> <tr><td>{{LANGUAGE}}</td><td>{{NAME}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody> </table>

Answer 1

Matlab, 326 bytes

With some group theory the idea is quite simple: Here the TL;DR Calculate all possible orders of elements of the group. Then find the biggest subgroup of a certain prime power order and "factorize" it out of the group, rinse, repeat.

function r=c(h,l)

                            %factorize group order
N=numel(L);
f=factor(N);
P=unique(f);                %prime factors
for k=1:numel(P);
    E(k)=sum(f==P(k));    %exponents of unique factors
end;

                            %calculate the order O of each element
O=L*0-1; 
l=L;
for k=2:N+1;

    l=h(l,L);

    O(l==L & O<0)=k-1
end;

%%

O=unique(O);               % (optional, just for speedupt)
R=[];
                           % for each prime,find the highest power that
                           % divides any of the orders of the element, and
                           % each time substract that from the remaining
                           % exponent in the prime factorization of the
                           % group order
for p=1:nnz(P);                          % loop over primes
    while E(p)>1;                        % loop over remaining exponent
        for e=E(p):-1:1;                 % find the highest exponent
            B=mod(O,P(p)^e)==0;          
            if any(B)
                R=[R,P(p)^e];            % if found, add to list
                O(B)=O(B)/(P(p)^e);
                E(p)=E(p)-e;
                break;
            end;
        end;
    end;
    if E(p)==1;
        R=[R,P(p)];
    end;
end;
r=sort(R)

Example inputs:

L = 0:3;
h=@(a,b)mod(a+b,4);
h=@(a,b)bitxor(a,b);
L = 0:80;
h=@(a,b)mod(mod(a,3)+mod(b,3),3)+mod(floor(a/3)+floor(b/3),3)*3+ mod(floor(a/9)+floor(b/9),9)*9; 

Golfed version:

function r=c(h,l);N=numel(L);f=factor(N);P=unique(f);for k=1:numel(P);E(k)=sum(f==P(k));end;O=L*0-1;l=L;for k=2:N+1;l=h(l,L);O(l==L&O<0)=k-1;end;R=[];for p=1:nnz(P);while E(p)>1;for e=E(p):-1:1;B=mod(O,P(p)^e)==0; if any(B);R=[R,P(p)^e]; O(B)=O(B)/(P(p)^e);E(p)=E(p)-e;break;end;end;end;if E(p)==1;R=[R,P(p)];end;end;r=sort(R)

Answer 2

GAP, 159 111 bytes

GAP allows us to simply construct a group by a multiplication table and compute its abelian invariants:

ai:=    # the golfed version states the function w/o assigning it
function(m,G)
  local t;
  t:=List(G,a->List(G,b->Position(G,m(a,b))));
  # t is inlined in the golfed version
  return AbelianInvariants(GroupByMultiplicationTable(t));
end;

The old version

The finitely presented group with generators G and relations a*b=m(a,b) (for all a, b from G) is the group (G,m) we started with. We can create it and compute its abelian invariants with GAP:

ai:=    # the golfed version states the function w/o assigning it
function(m,G)
  local F,n,rels;
  n:=Size(G);
  F:=FreeGroup(n);
  rels:=Union(Set([1..n],i->
                Set([1..n],j->
                  F.(i)*F.(j)/F.(Position(G,m(G[i],G[j]))) ) ));
  # rels is inlined in the golfed version
  return AbelianInvariants(F/rels);
end;

Examples

m1:=function(a,b) return (a+b) mod 4; end;
# I don't feel like implementing xor
m3:=function(a,b) return 9; end;
m4:=function(a,b)
  return (a+b) mod 3 # no need for inner mod
         + ((QuoInt(a,3)+QuoInt(b,3)) mod 3) * 3
         + ((QuoInt(a,9)+QuoInt(b,9)) mod 9) * 9;
  end;

Now we can do:

gap> ai(m1,[0..3]);
[ 4 ]

Actually, we are not restricted to using lists of integers. Using the correct domain, we can just use the general plus:

ai(\+,List(Integers mod 4));
[ 4 ]

So I can essentially do the second example using that its group is isomorphic to the additive group of the 2 dimensional vector space over the field with 2 elements:

gap> ai(\+,List(GF(2)^2));
[ 2, 2 ]

And the remaining examples:

gap> ai(m3,[9]);
[  ]
gap> ai(m4,[0..80]);
[ 3, 3, 9 ]

Additional remarks

In the old version, m did not need to define a group composition for G. If m(a,b)=m(a,c), that just says that b=c. So we could do ai(m1,[0..5]) and ai(m3,[5..15]). The new version will fail horrible in these cases, as will both versions if m returns values that are not in G.

If (G,m) is not abelian, we get a description of the abelianized version of it, that is its biggest abelian factor group:

gap> ai(\*,List(SymmetricGroup(4)));
[ 2 ]

This is what AbelianInvariants is usually used for, we would normally just call AbelianInvariants(SymmetricGroup(4)).

The golfed version

function(m,G)return AbelianInvariants(GroupByMultiplicationTable(List(G,a->List(G,b->Position(G,m(a,b))))));end