18
1
The cofactor matrix is the transpose of the Adjugate Matrix. The elements of this matrix are the cofactors of the original matrix.
The cofactor  (i.e. the element of the cofactor matrix at row i and column j) is the determinant of the submatrix formed by deleting the ith row and jth column from the original matrix, multiplied by (-1)^(i+j).
(i.e. the element of the cofactor matrix at row i and column j) is the determinant of the submatrix formed by deleting the ith row and jth column from the original matrix, multiplied by (-1)^(i+j).
For example, for the matrix
The element of the cofactor matrix at row 1 and column 2 is:
You can find info on what the determinant of a matrix is and how to calculate them here.
Challenge
Your goal is to output the cofactor matrix of an input matrix.
Note: Built-ins that evaluate cofactor matrices, or adjugate matrices, or determinants or anything similar are allowed.
Input
The matrix may be inputed as a command line argument, as a function parameter, in STDIN or in any way that is most appropriate for the language you use.
The matrix will be formatted as a list of lists, each sublist corresponding to one row, which contains factors ordered from left to right. Rows are ordered from top to bottom in the list.
For example, the matrix
a b
c d
will be represented by [[a,b],[c,d]].
You may replace the square brackets and commas with something else if it fits your language and is sensible (e.g. ((a;b);(c;d)))
Matrices will only contain integers (which can be negative).
Matrices will always be square (i.e. same number of rows and columns).
You may assume that the input will always be correct (i.e. no formatting problem, nothing other than integers, no empty matrix).
Output
The resulting cofactor matrix may be outputed to STDOUT, returned from a function, written to a file, or anything similar that naturally suits the language you use.
The cofactor matrix must be formatted in the exact same way the input matrices are given, e.g. [[d,-c],[-b,a]]. If you read a string, then you must return/output a string in which the matrix is formatted exactly like in the input. If you use something like e.g. a list of lists as input, then you must return a list of lists too.
Test cases
- Input:
[[1]]
Output: [[1]]
- Input:
[[1,2],[3,4]]
Output: [[4,-3],[-2,1]]
- Input:
[[-3,2,-5],[-1,0,-2],[3,-4,1]]
Output: [[-8,-5,4],[18,12,-6],[-4,-1,2]]
- Input:
[[3,-2,7,5,0],[1,-1,42,12,-10],[7,7,7,7,7],[1,2,3,4,5],[-3,14,-1,5,-9]]
Output:
[[9044,-13580,-9709,23982,-9737],[-1981,1330,3689,-3444,406],[14727,7113,2715,-9792,414],[-28448,-2674,-707,16989,14840],[-2149,2569,-2380,5649,-3689]]
Scoring
This is code-golf so the shortest answer in bytes wins.
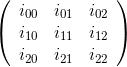
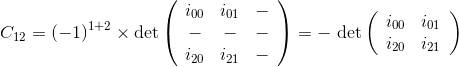
2I am not sure how to interpret the cofactor matrix must be formatted in the exact same way the input matrices are given for function submissions that get input from arguments and return a value. Do we read/return actual matrices or their string representations? – Dennis – 2015-12-16T22:51:45.680
1In short: if you read a string, then you must return/output a string in which the matrix is formatted exactly like in the input. If you use something like e.g. a list of lists, then you must return a list of lists too. – Fatalize – 2015-12-17T08:15:51.167
Does a 1x1 matrix really have a cofactor matrix? – Liam – 2015-12-18T07:11:55.027
Also your penultimate test case seems to be the adjugate matrix (the transpose of what it should be), unless I'm mistaken. – Liam – 2015-12-18T07:36:54.803
@ICanHazHats Correct, I fixed it, thanks. – Fatalize – 2015-12-18T08:35:44.857