Sprocket Science: Animating a Chain Drive System

Question

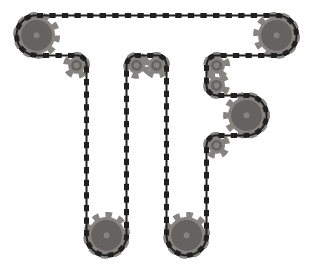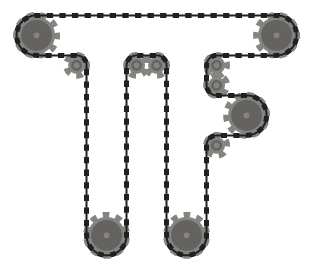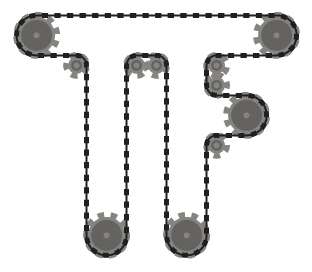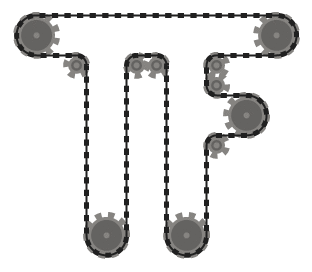
The goal of this challenge is to produce an animation of a chain drive system, comprised of a set of sprocket gears connected together by a chain.

General Requirements

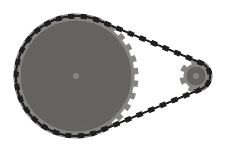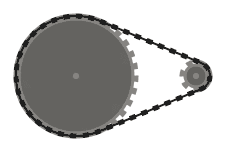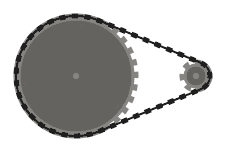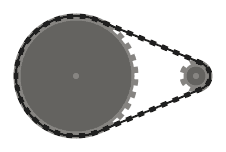
Your program will be given a list of sprockets, specified as (x, y, radius) triplets. The resulting chain drive system is comprised of these sprockets, connected together by a closed taut chain passing over each of them, in order. Your goal is to produce an infinitely looping animation, showing the system in motion. For example, given the input

(0, 0, 16),  (100, 0, 16),  (100, 100, 12),  (50, 50, 24),  (0, 100, 12)

, the output should look something like

.

The coordinate system should be such that the x-axis points right, and the y-axis points up. You may assume that the radii are even numbers greater than or equal to 8 (we'll see why this matters later.) You may also assume that there are at least two sprockets, and that the sprockets don't intersect one another. The units of the input are not too critical. All the examples and test cases in this post use pixels as the input units (so, for example, the radius of the middle sprocket in the previous figure is 24 pixels;) try not to deviate too much from these units. In the rest of the challenge, spatial quantities are understood to be given in the same units as the input—make sure to keep the proportions right! The dimensions of the output should be slightly bigger than the bounding box of all the sprockets, big enough so that the entire system is visible. In particular, the absolute positions of the sprockets should not affect the output; only their relative positions should (so, for example, if we shifted all the sprockets in the above example by the same amount, the output would remain the same.)

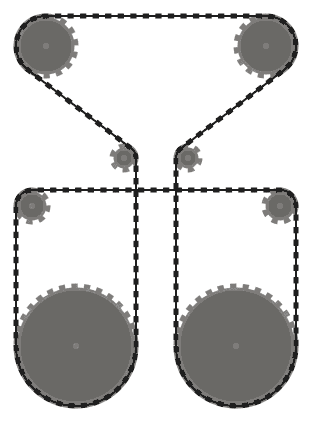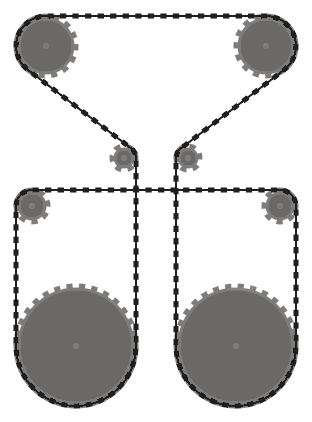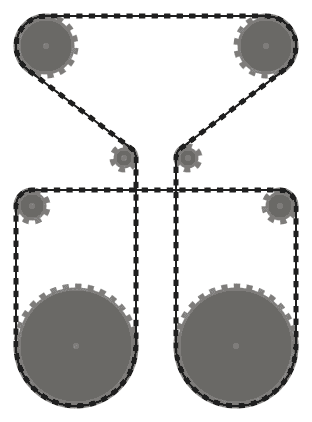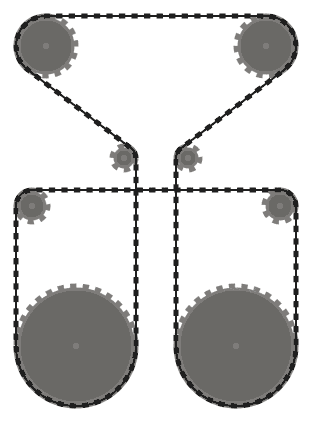
The chain should be tangent to the sprockets it passes over at all points of contact, and straight everywhere else. The chain should pass over the sprockets such that adjacent chain segments (that is, parts of the chain between two sprockets, that meet at the same sprocket) don't intersect each other.

.

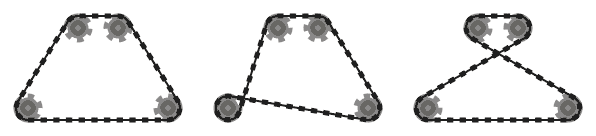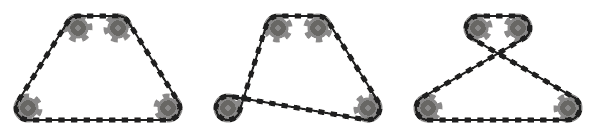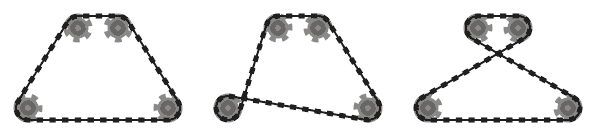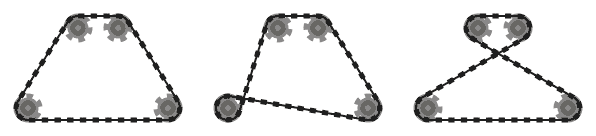For example, while the left system above is valid, the middle one is not, since the two adjacent chain segments that pass over the bottom left sprocket intersect. However, note that the right system is valid, since the two intersecting chain segments are not adjacent (this system is produced by a different input than the other two, though.)

To keep things simple(r), you may assume that no sprocket intersects the convex hull of its two neighboring sprockets, or the convex hulls of each of its neighbors and their other neighbor. In other words, the top sprocket in the diagram below may not intersect any of the shaded regions.

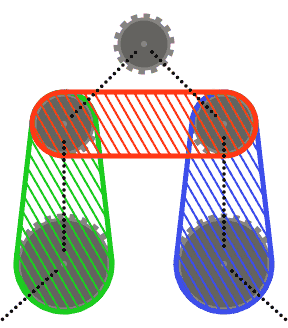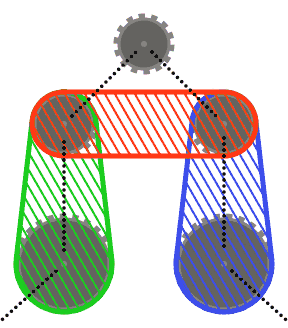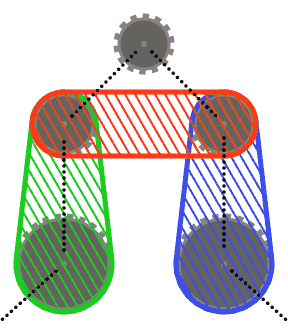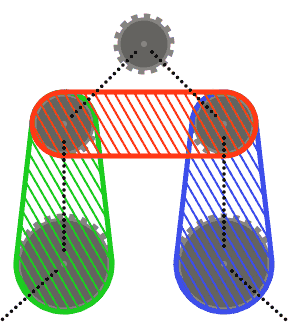
Chain segments may intersect sprockets other than the ones they pass over (such as in the last test case). In this case, the chain should always appear in front of the sprockets.

Visual Requirements

The chain should consist of a series of links of alternating widths. The width of the narrow link should be about 2, and the width of the wide link should be about 5. The length of both types of links should be about equal. The period of the chain, that is, the total length of a wide/narrow pair of links, should be the closest number to 4π that fits an integer number of times in the length of the chain. For example, if the length of the chain is 1,000, then its period should be 12.5, which is the closest number to 4π (12.566...) that fits an integer number of times (80) in 1,000. It's important for the period to fit an integer number of times in the chain's length, so that there are no artifacts at the point where the chain wraps around.

A sprocket of radius R should consist of three concentric parts: a central axle, which should be a circle of radius about 3; the sprocket's body, around the axle, which should be a circle of radius about R - 4.5; and the sprocket's rim, around the body, which should be a circle of radius about
R - 1.5. The rim should also contain the sprocket's teeth, which should have a width of about 4; the teeth's size and spacing should match the the sizes of the chain links, so that they enmesh neatly.

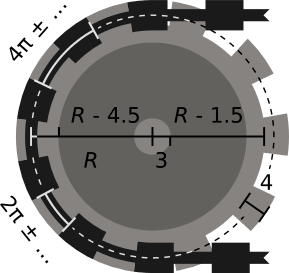
The period of the sprocket's teeth, that is, the distance between two consecutive teeth along the circumference of the sprocket, should match the period of the chain. Since the period is about 4π, and since the radius of the sprocket is guaranteed to be even, the period should fit in the sprocket's circumference an almost-integer number of times, so that there shouldn't be any noticeable artifacts at the point where the sprocket's teeth wrap around.

You may use any combination of colors for the chain, the different parts of the sprocket, and the background, as long as they are easily distinguishable. The background may be transparent. The examples in this post use #202020 for the chain, #868481 for the sprocket's axle and rim, and #646361 for the sprocket's body.

Animation Requirements

The first sprocket in the input list should rotate clockwise; the rest of the sprockets should rotate accordingly. The chain should move at a speed of about 16π (about 50) units per second; the frame rate is up to you, but the animation should look smooth enough.

The animation should loop seamlessly.

Conformance

Some of the visual attributes and proportions are intentionally specified only roughly—you don't have to match them exactly. Your program's output doesn't have to be a pixel-to-pixel replica of the examples given here, but it should look similar. In particular, the exact proportions of the chain and the sprockets, and the exact shape of the chain's links and sprocket's teeth, are flexible.

The most important points to follow are these:

• The chain should pass over the sprockets, in input order, from the correct direction.
• The chain should be tangent to the sprockets at all points of contact.
• The links of the chain and the teeth of the sprockets should enmesh neatly, at least up to correct spacing and phase.
• The spacing between the links of the chain, and the teeth of the sprockets, should be such that there are no noticeable artifacts at the point where they wrap around.
• The sprockets should rotate in the correct direction.
• The animation should loop seamlessly.

As a final note, while, technically, the goal of this challenge is to write the shortest code, if you feel like getting creative and producing a more elaborate output, by all means, go for it!

Challenge

Write a program or a function, taking a list of sprockets, and producing a corresponding chain drive system animation, as described above.

Input and Output

You may take the input through the command line, through STDIN, as function arguments, or using an equivalent method. You may use any convenient format for the input, but make sure to specify it in your post.

As output, you may display the animation directly, produce an animation file (e.g., an animated GIF), or produce a sequence of frame files (however, there's a small penalty in this case; see below.) If you use file output, make sure the number of frames is reasonable (the examples in this post use very few frames;) the number of frames doesn't have to be minimal, but you shouldn't produce too many superfluous frames. If you output a sequence of frames, make sure to specify the frame rate in your post.

Score

This is code-golf. The shortest answer, in bytes, wins.

+10% Penalty  If your program produces a sequence of frames as output, instead of displaying the animation directly or producing a single animation file, add 10% to your score.

Test Cases

Test 1

(0, 0, 26),  (120, 0, 26)

Test 2

(100, 100, 60),  (220, 100, 14)

Test 3

(100, 100, 16),  (100, 0, 24),  (0, 100, 24),  (0, 0, 16)

Test 4

(0, 0, 60),  (44, 140, 16),  (-204, 140, 16),  (-160, 0, 60),  (-112, 188, 12),
(-190, 300, 30),  (30, 300, 30),  (-48, 188, 12)

Test 5

(0, 128, 14),  (46.17, 63.55, 10),  (121.74, 39.55, 14),  (74.71, -24.28, 10),
(75.24, -103.55, 14),  (0, -78.56, 10),  (-75.24, -103.55, 14),  (-74.71, -24.28, 10),
(-121.74, 39.55, 14),  (-46.17, 63.55, 10)

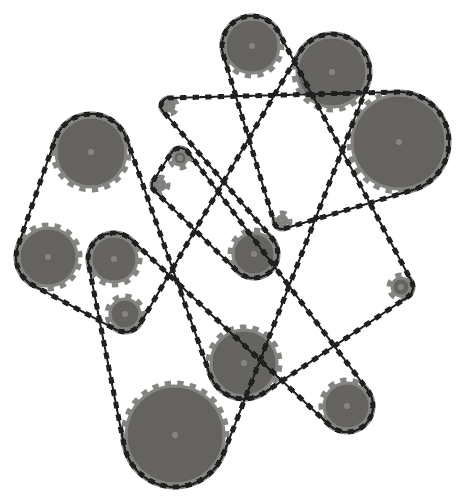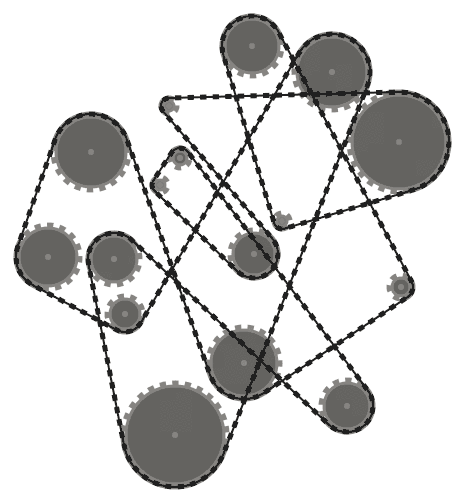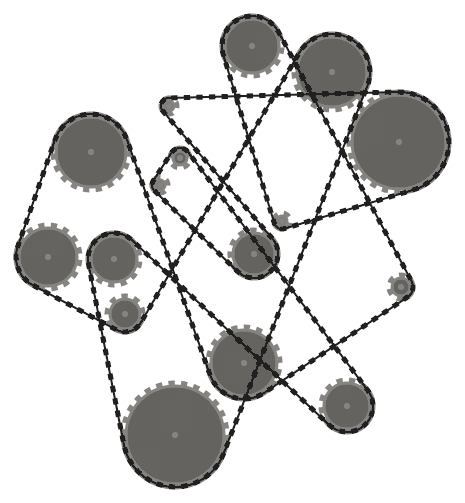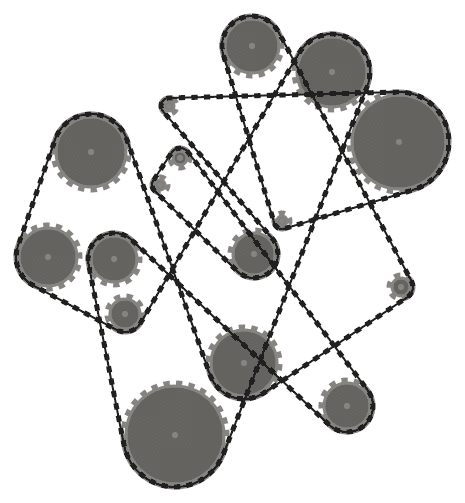
Test 6

(367, 151, 12),  (210, 75, 36),  (57, 286, 38),  (14, 181, 32),  (91, 124, 18),
(298, 366, 38),  (141, 3, 52),  (80, 179, 26),  (313, 32, 26),  (146, 280, 10),
(126, 253, 8),  (220, 184, 24),  (135, 332, 8),  (365, 296, 50),  (248, 217, 8),
(218, 392, 30)

---

Answer 1

JavaScript (ES6), 2557 1915 1897 1681 bytes

This isn't super-duper golfed really; it's minified - partly by hand - but that's nothing special. It could no doubt be shorter if I'd golfed it more before minifying, but I've spent (more than) enough time on this already.

Edit: Ok, so I spent more time on it and golfed the code more before minifying (very manually this time). The code's still using the same approach and overall structure, but even so I still ended up saving 642 bytes. Not too shabby, if I do say so myself. Probably missed some byte-saving opportunities, but at this point even I'm not sure how it works anymore. The only thing that's different in terms of output, is that it now uses slightly different colors that could be written more tersely.

Edit 2 (much later): Saved 18 bytes. Thanks to ConorO'Brien in the comments for pointing out the blindingly obvious that I'd totally missed.

Edit 3: So, I figured I'd reverse engineer my own code, because, frankly, I couldn't remember how I'd done it, and I lost the ungolfed versions. So I went through, and lo and behold found another 316 bytes to save by restructuring and doing some micro-golfing.

R=g=>{with(Math){V=(x,y,o)=>o={x,y,l:sqrt(x*x+y*y),a:v=>V(x+v.x,y+v.y),s:v=>o.a(v.m(-1)),m:f=>V(x*f,y*f),t:r=>V(x*cos(r)-y*sin(r),x*sin(r)+y*cos(r)),c:v=>x*v.y-y*v.x,toString:_=>x+','+y};a='appendChild',b='setAttribute';S=(e,a)=>Object.keys(a).map(n=>e[b](n,a[n]))&&e;T=(t,a)=>S(k.createElementNS('http://www.w3.org/2000/svg',t),a);C=(e,a)=>S(e.cloneNode(),a);P=a=>T('path',(a.fill='none',a));w=h=-(x=y=1/0);G=g.map((a,g)=>(g=V(...a))&&(u=(g.r=a[2])+5,x=min(x,g.x-u),y=min(y,g.y-u),w=max(w,g.x+u),h=max(h,g.y+u))&&g);k=document;I=k[a].bind(k.body[a](T('svg',{width:w-x,height:h-y}))[a](T('g',{transform:`translate(${-x},${h})scale(1,-1)`})));L=(c)=>(h=G.length)&&G.map((g,i)=>c(G[i],G[i?i-1:h-1],G[(i+1)%h]))&&L;l='';L((g,p,n)=>g.f=p.s(g).c(n.s(g))>0)((g,a,n)=>{d=g.s(n),y=x=1/d.l;g.f!=n.f?(a=asin((g.r+n.r)*x),g.f?(x=-x,a=-a):(y=-y)):(a=asin((g.r-n.r)*x),g.f&&(x=y=-x,a=-a));t=d.t(a+PI/2);g.o=t.m(x*g.r).a(g);n.i=t.m(y*n.r).a(n)})((g,p,n)=>{z='#888';d=(l,s,e)=>`A${g.r},${g.r} 0 ${1*l},${1*s} ${e}`;e=(f,r)=>T('circle',{cx:g.x,cy:g.y,r,fill:f});g.k=p.o.s(n.i).l<g.i.s(g.o).l;w=d(g.k,!g.f,g.o);g.j=`${w}L${n.i}`;l+=g.j;I(e(z,g.r-1.5));g.g=I(P({d:`M${g.i}${w}${d(!g.k,!g.f,g.i)}`,stroke:z,'stroke-width':5}));g.h=I(C(g.g,{d:`M${g.i}${g.j}`,stroke:'#222'}));I(e('#666',g.r-4.5));I(e(z,3))});t=e=>e.getTotalLength(),u='stroke-dasharray',v='stroke-dashoffset',f=G[0];l=I(C(f.h,{d:'M'+f.i+l,'stroke-width':2}));s=f.w=t(l)/round(t(l)/(4*PI))/2;X=8*s;Y=f.v=0;L((g,p)=>{g.g[b](u,s);g.h[b](u,s);g==f||(g.w=p.w+t(p.h),g.v=p.v+t(p.h));g.g[b](v,g.w);g.h[b](v,g.v);g.h[a](C(g.g[a](T('animate',{attributeName:v,from:g.w+X,to:g.w+Y,repeatCount:'indefinite',dur:'1s'})),{from:g.v+X,to:g.v+Y}))})}}

The function above appends an SVG element (including animations) to the document. E.g. to display the 2nd test case:

R([[100, 100, 60],  [220, 100, 14]]);

Seems to work a treat - at least here in Chrome.

Try it in the snippet below (clicking the buttons will draw each of OP's test cases).

R=g=>{with(Math){V=(x,y,o)=>o={x,y,l:sqrt(x*x+y*y),a:v=>V(x+v.x,y+v.y),s:v=>o.a(v.m(-1)),m:f=>V(x*f,y*f),t:r=>V(x*cos(r)-y*sin(r),x*sin(r)+y*cos(r)),c:v=>x*v.y-y*v.x,toString:_=>x+','+y};a='appendChild',b='setAttribute';S=(e,a)=>Object.keys(a).map(n=>e[b](n,a[n]))&&e;T=(t,a)=>S(k.createElementNS('http://www.w3.org/2000/svg',t),a);C=(e,a)=>S(e.cloneNode(),a);P=a=>T('path',(a.fill='none',a));w=h=-(x=y=1/0);G=g.map((a,g)=>(g=V(...a))&&(u=(g.r=a[2])+5,x=min(x,g.x-u),y=min(y,g.y-u),w=max(w,g.x+u),h=max(h,g.y+u))&&g);k=document;I=k[a].bind(k.body[a](T('svg',{width:w-x,height:h-y}))[a](T('g',{transform:`translate(${-x},${h})scale(1,-1)`})));L=(c)=>(h=G.length)&&G.map((g,i)=>c(G[i],G[i?i-1:h-1],G[(i+1)%h]))&&L;l='';L((g,p,n)=>g.f=p.s(g).c(n.s(g))>0)((g,a,n)=>{d=g.s(n),y=x=1/d.l;g.f!=n.f?(a=asin((g.r+n.r)*x),g.f?(x=-x,a=-a):(y=-y)):(a=asin((g.r-n.r)*x),g.f&&(x=y=-x,a=-a));t=d.t(a+PI/2);g.o=t.m(x*g.r).a(g);n.i=t.m(y*n.r).a(n)})((g,p,n)=>{z='#888';d=(l,s,e)=>`A${g.r},${g.r} 0 ${1*l},${1*s} ${e}`;e=(f,r)=>T('circle',{cx:g.x,cy:g.y,r,fill:f});g.k=p.o.s(n.i).l<g.i.s(g.o).l;w=d(g.k,!g.f,g.o);g.j=`${w}L${n.i}`;l+=g.j;I(e(z,g.r-1.5));g.g=I(P({d:`M${g.i}${w}${d(!g.k,!g.f,g.i)}`,stroke:z,'stroke-width':5}));g.h=I(C(g.g,{d:`M${g.i}${g.j}`,stroke:'#222'}));I(e('#666',g.r-4.5));I(e(z,3))});t=e=>e.getTotalLength(),u='stroke-dasharray',v='stroke-dashoffset',f=G[0];l=I(C(f.h,{d:'M'+f.i+l,'stroke-width':2}));s=f.w=t(l)/round(t(l)/(4*PI))/2;X=8*s;Y=f.v=0;L((g,p)=>{g.g[b](u,s);g.h[b](u,s);g==f||(g.w=p.w+t(p.h),g.v=p.v+t(p.h));g.g[b](v,g.w);g.h[b](v,g.v);g.h[a](C(g.g[a](T('animate',{attributeName:v,from:g.w+X,to:g.w+Y,repeatCount:'indefinite',dur:'1s'})),{from:g.v+X,to:g.v+Y}))})}}


// ========================
// Test code

var testCases = [
  [[0, 0, 16],  [100, 0, 16],  [100, 100, 12],  [50, 50, 24],  [0, 100, 12]],
  [[0, 0, 26],  [120, 0, 26]],
  [[100, 100, 60],  [220, 100, 14]],
  [[100, 100, 16],  [100, 0, 24],  [0, 100, 24],  [0, 0, 16]],
  [[0, 0, 60],  [44, 140, 16],  [-204, 140, 16],  [-160, 0, 60],  [-112, 188, 12], [-190, 300, 30],  [30, 300, 30],  [-48, 188, 12]],
  [[0, 128, 14],  [46.17, 63.55, 10],  [121.74, 39.55, 14],  [74.71, -24.28, 10], [75.24, -103.55, 14],  [0, -78.56, 10],  [-75.24, -103.55, 14],  [-74.71, -24.28, 10], [-121.74, 39.55, 14],  [-46.17, 63.55, 10]],
  [[367, 151, 12],  [210, 75, 36],  [57, 286, 38],  [14, 181, 32],  [91, 124, 18], [298, 366, 38],  [141, 3, 52],  [80, 179, 26],  [313, 32, 26],  [146, 280, 10], [126, 253, 8],  [220, 184, 24],  [135, 332, 8],  [365, 296, 50],  [248, 217, 8], [218, 392, 30]]
];

function clear() {
  var buttons = document.createElement('div');
  document.body.innerHTML = "";
  document.body.appendChild(buttons);
  testCases.forEach(function (data, i) {
    var button = document.createElement('button');
    button.innerHTML = String(i);
    button.onclick = function () {
      clear();
      R(data);
      return false;
    };
    buttons.appendChild(button);
  });
}

clear();

The code draws the chain and gear teeth as a dashed strokes. It then uses animate elements to animate the stroke-dashoffset attribute. The resulting SVG element is self-contained; there's no JS-driven animation or CSS styling.

To make things line up nicely, each gear's ring of teeth is actually drawn as a path consisting of two arcs, so the path can start right at the tangent point where the chain touches. This makes it a lot simpler to line it up.

Furthermore, it seems there's a lot of rounding errors when using SVG's dashed strokes. At least, that's what I saw; the longer the chain, the worse it'd mesh with each successive gear. So to minimize the issue, the chain is actually made up of several paths. Each path consists of an arcing segment around one gear and a straight line to the next gear. Their dash-offsets are calculated to match. The thin "inner" part of the chain, however, is just a single looping path, since it isn't animated.

Answer 2

C# 3566 bytes

Not golfed at all, but works (I think)

Ungolfed in edit history.

Uses Magick.NET to render gif.

class S{public float x,y,r;public bool c;public double i,o,a=0,l=0;public S(float X,float Y,float R){x=X;y=Y;r=R;}}class P{List<S>q=new List<S>();float x=float.MaxValue,X=float.MinValue,y=float.MaxValue,Y=float.MinValue,z=0,Z=0,N;int w=0,h=0;Color c=Color.FromArgb(32,32,32);Pen p,o;Brush b,n,m;List<PointF>C;double l;void F(float[][]s){p=new Pen(c,2);o=new Pen(c,5);b=new SolidBrush(c);n=new SolidBrush(Color.FromArgb(134,132,129));m=new SolidBrush(Color.FromArgb(100,99,97));for(int i=0;i<s.Length;i++){float[]S=s[i];q.Add(new S(S[0],S[1],S[2]));if(S[0]-S[2]<x)x=S[0]-S[2];if(S[1]-S[2]<y)y=S[1]-S[2];if(S[0]+S[2]>X)X=S[0]+S[2];if(S[1]+S[2]>Y)Y=S[1]+S[2];}q[0].c=true;z=-x+16;Z=-y+16;w=(int)(X-x+32);h=(int)(Y-y+32);for(int i=0;i<=q.Count;i++)H(q[i%q.Count],q[(i+1)%q.Count],q[(i+2)%q.Count]);C=new List<PointF>();for(int i=0;i<q.Count;i++){S g=q[i],k=q[(i+1)%q.Count];if(g.c)for(double a=g.i;a<g.i+D(g.o,g.i);a+=Math.PI/(2*g.r)){C.Add(new PointF((float)(g.x+z+g.r*Math.Cos(a)),(float)(g.y+Z+g.r*Math.Sin(a))));}else
for(double a=g.o+D(g.i,g.o);a>g.o;a-=Math.PI/(2*g.r)){C.Add(new PointF((float)(g.x+z+g.r*Math.Cos(a)),(float)(g.y+Z+g.r*Math.Sin(a))));}C.Add(new PointF((float)(g.x+z+g.r*Math.Cos(g.o)),(float)(g.y+Z+g.r*Math.Sin(g.o))));C.Add(new PointF((float)(k.x+z+k.r*Math.Cos(k.i)),(float)(k.y+Z+k.r*Math.Sin(k.i))));k.l=E(C);}l=E(C);N=(float)(K(l)/10.0);o.DashPattern=new float[]{N,N};double u=q[0].i;for(int i=0;i<q.Count;i++){S g=q[i];double L=g.l/(N*5);g.a=g.i+((1-(L%2))/g.r*Math.PI*2)*(g.c?1:-1);}List<MagickImage>I=new List<MagickImage>();for(int i=0;i<t;i++){using(Bitmap B=new Bitmap(w,h)){using(Graphics g=Graphics.FromImage(B)){g.Clear(Color.White);g.SmoothingMode=System.Drawing.Drawing2D.SmoothingMode.AntiAlias;foreach(S U in q){float R=U.x+z,L=U.y+Z,d=7+2*U.r;PointF[]f=new PointF[4];for(double a=(i*(4.0/t));a<2*U.r;a+=4){double v=U.a+((U.c?-a:a)/U.r*Math.PI),j=Math.PI/U.r*(U.c?1:-1),V=v+j,W=V+j,r=U.r+3.5;f[0]=new PointF(R,L);f[1]=new PointF(R+(float)(r*Math.Cos(v)),L+(float)(r*Math.Sin(v)));f[2]=new PointF(R+(float)(r*Math.Cos(V)),L+(float)(r*Math.Sin(V)));f[3]=new PointF(R+(float)(r*Math.Cos(W)),L+(float)(r*Math.Sin(W)));g.FillPolygon(n,f);}d=2*(U.r-1.5f);g.FillEllipse(n,R-d/2,L-d/2,d,d);d=2*(U.r-4.5f);g.FillEllipse(m,R-d/2,L-d/2,d,d);d=6;g.FillEllipse(n,R-d/2,L-d/2,d,d);}g.DrawLines(p,C.ToArray());o.DashOffset=(N*2.0f/t)*i;g.DrawLines(o,C.ToArray());B.RotateFlip(RotateFlipType.RotateNoneFlipY);B.Save(i+".png",ImageFormat.Png);I.Add(new MagickImage(B));}}}using(MagickImageCollection collection=new MagickImageCollection()){foreach(MagickImage i in I){i.AnimationDelay=5;collection.Add(i);}QuantizeSettings Q=new QuantizeSettings();Q.Colors=256;collection.Quantize(Q);collection.Optimize();collection.Write("1.gif");}}int t=5;double D(double a,double b){double P=Math.PI,r=a-b;while(r<0)r+=2*P;return r%(2*P);}double E(List<PointF> c){double u=0;for(int i=0;i<c.Count-1;i++){PointF s=c[i];PointF t=c[i+1];double x=s.X-t.X,y=s.Y-t.Y;u+=Math.Sqrt(x*x+y*y);}return u;}double K(double L){double P=4*Math.PI;int i=(int)(L/P);float a=(float)L/i,b=(float)L/(i+1);if(Math.Abs(P-a)<Math.Abs(P-b))return a;return b;}void H(S a,S b,S c){double A=0,r=0,d=b.x-a.x,e=b.y-a.y,f=Math.Atan2(e,d)+Math.PI/2,g=Math.Atan2(e,d)-Math.PI/2,h=Math.Atan2(-e,-d)-Math.PI/2,i=Math.Atan2(-e,-d)+Math.PI/2;double k=c.x-b.x,n=c.y-b.y,l=Math.Sqrt(d*d+e*e);A=D(Math.Atan2(n,k),Math.Atan2(-e,-d));bool x=A>Math.PI!=a.c;b.c=x!=a.c;if(a.r!=b.r)r=a.r+(x?b.r:-b.r);f-=Math.Asin(r/l);g+=Math.Asin(r/l);h+=Math.Asin(r/l);i-=Math.Asin(r/l);b.i=x==a.c?h:i;a.o=a.c?g:f;}}

Class P has a function F; Example:

static void Main(string[]a){
P p=new P();
float[][]s=new float[][]{
new float[]{10,200,20},
new float[]{240,200,20},
new float[]{190,170,10},
new float[]{190,150,10},
new float[]{210,120,20},
new float[]{190,90,10},
new float[]{160,0,20},
new float[]{130,170,10},
new float[]{110,170,10},
new float[]{80,0,20},
new float[]{50,170,10}
};
p.F(s);}

Answer 3

JavaScript (ES6) 1626 bytes

This solution is the result of reverse engineering of @Flambino's solution, I post it with his accord.

R=g=>{with(Math){v='stroke';j=v+'-dasharray';q=v+'-dashoffset';m='appendChild';n='getTotalLength';b='setAttribute';z='#888';k=document;V=(x,y,r,o)=>o={x,y,r,l:sqrt(x*x+y*y),a:v=>V(x+v.x,y+v.y),s:v=>o.a(v.m(-1)),m:f=>V(x*f,y*f),t:r=>V(x*cos(r)-y*sin(r),x*sin(r)+y*cos(r)),c:v=>x*v.y-y*v.x,toString:_=>x+','+y};S=(e,a)=>Object.keys(a).map(n=>e[b](n,a[n]))&&e;T=(t,a)=>S(k.createElementNS('http://www.w3.org/2000/svg',t),a);C=(e,a)=>S(e.cloneNode(),a);w=h=-(x=y=1/0);G=g.map((a,g)=>(g=V(...a))&&(u=(g.r=a[2])+5,x=min(x,g.x-u),y=min(y,g.y-u),w=max(w,g.x+u),h=max(h,g.y+u))&&g);f=G[0];w-=x;h-=y;s=T('svg',{width:w,height:h,viewBox:x+' '+y+' '+w+' '+h,transform:'scale(1,-1)'});c='';L=(c)=>(h=G.length)&&G.map((g,i)=>c(G[i],G[(h+i-1)%h],G[(i+1)%h]))&&L;L((g,p,n)=>g.w=(p.s(g).c(n.s(g))>0))((g,p,n)=>{d=g.s(n),y=x=1/d.l;g.w!=n.w?(p=asin((g.r+n.r)*x),g.w?(x=-x,p=-p):(y=-y)):(p=asin((g.r-n.r)*x),g.w&&(x=y=-x,p=-p));t=d.t(p+PI/2);g.o=t.m(x*g.r).a(g);n.i=t.m(y*n.r).a(n)})((g,p,n)=>{l=(p.o.s(n.i).l<g.i.s(g.o).l);d=(l,e)=>`A${g.r} ${g.r} 0 ${+l} ${+!g.w} ${e}`;a=d(l,g.o);e=(f,r)=>T('circle',{cx:g.x,cy:g.y,r,fill:f});c+=a+'L'+n.i;s[m](e(z,g.r-1.5));s[m](e('#666',g.r-4.5));s[m](e(z,3));g.p=s[m](C(g.e=s[m](T('path',{d:'M'+g.i+a+d(!l,g.i),fill:'none',[v]:z,[v+'-width']:5})),{d:'M'+g.i+a+'L'+n.i,[v]:'#222'}))});c=C(f.p,{d:'M'+f.i+c,[v+'-width']:2});g=c[n]();y=8*(x=g/round(g/(4*PI))/2);f.g=x;f.h=0;L((g,p)=>{g!=f&&(g.g=p.g+p.p[n](),g.h=p.h+p.p[n]());S(g.p,{[j]:x,[q]:g.h})[m](C(S(g.e,{[j]:x,[q]:g.g})[m](T('animate',{attributeName:[q],from:g.g+y,to:g.g,repeatCount:'indefinite',dur:'1s'})),{from:g.h+y,to:g.h}))});k.body[m](s)[m](c)}}

The ungolfed version:

class Vector {

    constructor(x, y) {
        this.x = x;
        this.y = y;
        this.length = Math.sqrt(x * x + y * y);
    }

    add(vector) {

        return new Vector(this.x + vector.x, this.y + vector.y);
    }

    subtract(vector) {

        return new Vector(this.x - vector.x, this.y - vector.y);
    }

    multiply(scalar) {

        return new Vector(this.x * scalar, this.y * scalar);
    }

    rotate(radians) {

        const cos = Math.cos(radians);
        const sin = Math.sin(radians);

        return new Vector(this.x * cos - this.y * sin, this.x * sin + this.y * cos);
    }

    cross(vector) {

        return this.x * vector.y - this.y * vector.x;
    }

    toString() {

        return `${this.x},${this.y}`;
    }
}

class Gear {

    constructor(x, y, radius) {
        this.x = x;
        this.y = y;
        this.radius = radius;
    }

    getVector() {

        return new Vector(this.x, this.y);
    }
}

const setAttributes = (element, attributes) => {

    Object.keys(attributes).forEach((attribute) => {
        element.setAttribute(attribute, attributes[attribute]);
    });
};

const createElement = (tagName, attributes) => {

    const element = document.createElementNS('http://www.w3.org/2000/svg', tagName);

    setAttributes(element, attributes);

    return element;
};

const cloneElement = (element, attributes) => {

    const clone = element.cloneNode();

    setAttributes(clone, attributes);

    return clone;
};

const createPath = (attributes) => {

    return createElement('path', {
        ...attributes,
        fill: 'none'
    });
};

const createCircle = (cx, cy, r, fill) => {

    return createElement('circle', {
        cx,
        cy,
        r,
        fill
    });
};

const loopGears = (gears, callback) => {

    const length = gears.length;

    gears.forEach((gear, index) => {

        const prevGear = gears[(length + index - 1) % length];
        const nextGear = gears[(index + 1) % length];

        callback(gear, prevGear, nextGear);
    });
};

const arcDescription = (radius, largeArcFlag, sweepFlag, endVector) => {

    return `A${radius} ${radius} 0 ${+largeArcFlag} ${+sweepFlag} ${endVector}`;
};

const renderGears = (data) => {

    let x = Infinity;
    let y = Infinity;
    let w = -Infinity;
    let h = -Infinity;

    const gears = data.map((params) => {

        const gear = new Gear(...params);
        const unit = params[2] + 5;

        x = Math.min(x, gear.x - unit);
        y = Math.min(y, gear.y - unit);
        w = Math.max(w, gear.x + unit);
        h = Math.max(h, gear.y + unit);

        return gear;
    });

    const firstGear = gears[0];

    w -= x;
    h -= y;

    const svg = createElement('svg', {
        width: w,
        height: h,
        viewBox: `${x} ${y} ${w} ${h}`,
        transform: `scale(1,-1)`
    });

    let chainPath = '';

    loopGears(gears, (gear, prevGear, nextGear) => {

        const gearVector = gear.getVector();
        const prevGearVector = prevGear.getVector().subtract(gearVector);
        const nextGearVector = nextGear.getVector().subtract(gearVector);

        gear.sweep = (prevGearVector.cross(nextGearVector) > 0);
    });

    loopGears(gears, (gear, prevGear, nextGear) => {

        const diffVector = gear.getVector().subtract(nextGear.getVector());

        let angle = 0;
        let x = 1 / diffVector.length;
        let y = x;

        if (gear.sweep === nextGear.sweep) {

            angle = Math.asin((gear.radius - nextGear.radius) * x);

            if (gear.sweep) {
                x = -x;
                y = -y;
                angle = -angle;
            }
        } else {

            angle = Math.asin((gear.radius + nextGear.radius) * x);

            if (gear.sweep) {
                x = -x;
                angle = -angle;
            } else {
                y = -y;
            }
        }

        const perpendicularVector = diffVector.rotate(angle + Math.PI / 2);

        gear.out = perpendicularVector.multiply(x * gear.radius).add(gear.getVector());
        nextGear.in = perpendicularVector.multiply(y * nextGear.radius).add(nextGear.getVector());
    });

    loopGears(gears, (gear, prevGear, nextGear) => {

        const largeArcFlag = (prevGear.out.subtract(nextGear.in).length < gear.in.subtract(gear.out).length);
        const arcPath = arcDescription(gear.radius, largeArcFlag, !gear.sweep, gear.out);

        const gearExterior = createCircle(gear.x, gear.y, gear.radius - 1.5, '#888');
        const gearInterior = createCircle(gear.x, gear.y, gear.radius - 4.5, '#666');
        const gearCenter = createCircle(gear.x, gear.y, 3, '#888');

        const gearTeeth = createPath({
            d: `M${gear.in}${arcPath}${arcDescription(gear.radius, !largeArcFlag, !gear.sweep, gear.in)}`,
            stroke: '#888',
            'stroke-width': 5
        });

        const chainParts = cloneElement(gearTeeth, {
            d: `M${gear.in}${arcPath}L${nextGear.in}`,
            stroke: '#222'
        });

        gear.teeth = gearTeeth;
        gear.chainParts = chainParts;

        chainPath += `${arcPath}L${nextGear.in}`;

        svg.appendChild(gearExterior);
        svg.appendChild(gearInterior);
        svg.appendChild(gearCenter);
        svg.appendChild(gearTeeth);
        svg.appendChild(chainParts);
    });

    const chain = cloneElement(firstGear.chainParts, {
        d: 'M' + firstGear.in + chainPath,
        'stroke-width': 2
    });

    const chainLength = chain.getTotalLength();
    const chainUnit = chainLength / Math.round(chainLength / (4 * Math.PI)) / 2;
    const animationOffset = 8 * chainUnit;

    loopGears(gears, (gear, prevGear) => {

        if (gear === firstGear) {
            gear.teethOffset = chainUnit;
            gear.chainOffset = 0;
        } else {
            gear.teethOffset = prevGear.teethOffset + prevGear.chainParts.getTotalLength();
            gear.chainOffset = prevGear.chainOffset + prevGear.chainParts.getTotalLength();
        }

        setAttributes(gear.teeth, {
            'stroke-dasharray': chainUnit,
            'stroke-dashoffset': gear.teethOffset
        });

        setAttributes(gear.chainParts, {
            'stroke-dasharray': chainUnit,
            'stroke-dashoffset': gear.chainOffset
        });

        const animate = createElement('animate', {
            attributeName: 'stroke-dashoffset',
            from: gear.teethOffset + animationOffset,
            to: gear.teethOffset,
            repeatCount: 'indefinite',
            dur: '1s'
        });

        const cloneAnimate = cloneElement(animate, {
            from: gear.chainOffset + animationOffset,
            to: gear.chainOffset
        });

        gear.teeth.appendChild(animate);
        gear.chainParts.appendChild(cloneAnimate);
    });

    svg.appendChild(chain);
    document.body.appendChild(svg);
};

var testCases = [
    [[0, 0, 16],  [100, 0, 16],  [100, 100, 12],  [50, 50, 24],  [0, 100, 12]],
    [[0, 0, 26],  [120, 0, 26]],
    [[100, 100, 60],  [220, 100, 14]],
    [[100, 100, 16],  [100, 0, 24],  [0, 100, 24],  [0, 0, 16]],
    [[0, 0, 60],  [44, 140, 16],  [-204, 140, 16],  [-160, 0, 60],  [-112, 188, 12], [-190, 300, 30],  [30, 300, 30],  [-48, 188, 12]],
    [[0, 128, 14],  [46.17, 63.55, 10],  [121.74, 39.55, 14],  [74.71, -24.28, 10], [75.24, -103.55, 14],  [0, -78.56, 10],  [-75.24, -103.55, 14],  [-74.71, -24.28, 10], [-121.74, 39.55, 14],  [-46.17, 63.55, 10]],
    [[367, 151, 12],  [210, 75, 36],  [57, 286, 38],  [14, 181, 32],  [91, 124, 18], [298, 366, 38],  [141, 3, 52],  [80, 179, 26],  [313, 32, 26],  [146, 280, 10], [126, 253, 8],  [220, 184, 24],  [135, 332, 8],  [365, 296, 50],  [248, 217, 8], [218, 392, 30]]
];

function clear() {
    var buttons = document.createElement('div');
    document.body.innerHTML = "";
    document.body.appendChild(buttons);
    testCases.forEach(function (data, i) {
        var button = document.createElement('button');
        button.innerHTML = String(i);
        button.onclick = function () {
            clear();
            renderGears(data);
            return false;
        };
        buttons.appendChild(button);
    });
}

clear();