21
1
Take a look at this image. Specifically, at how the holes on the ends are arranged.
Notice how the pipes in this image are packed in a hexagonal pattern. It is known that in 2D, a hexagonal lattice is the densest packing of circles. In this challenge, we will be focusing on minimizing the perimeter of a packing of circles. One useful way to visualize the perimeter is to imagine putting a rubber band around the collection of circles.
The Task
Given a positive integer n as input, show a collection of n circles packed as tightly as possible.
Rules and Clarifications
- Assume circles have a diameter of 1 unit.
- The variable to be minimized is the length of the perimeter, which is defined to be the convex hull of the centers of the circles in the group. Take a look at this image:
The three circles in a straight line have a perimeter of 4 (the convex hull is a 2x0 rectangle, and the 2 is counted twice), those arranged in a 120-degree angle have a perimeter of about 3.85, and the triangle has a perimeter of only 3 units. Note that I am ignoring the additional pi units that the actual perimeter would be because I'm only looking at the circles' centers, not their edges.
- There may (and almost certainly will be) multiple solutions for any given
n. You may output any of these at your discretion. Orientation does not matter. - The circles must be on a hexagonal lattice.
- The circles must be at least 10 pixels in diameter, and may be filled or not.
- You may write either a program or a function.
- Input may be taken through STDIN, as a function argument, or closest equivalent.
- The output may be displayed or output to a file.
Examples
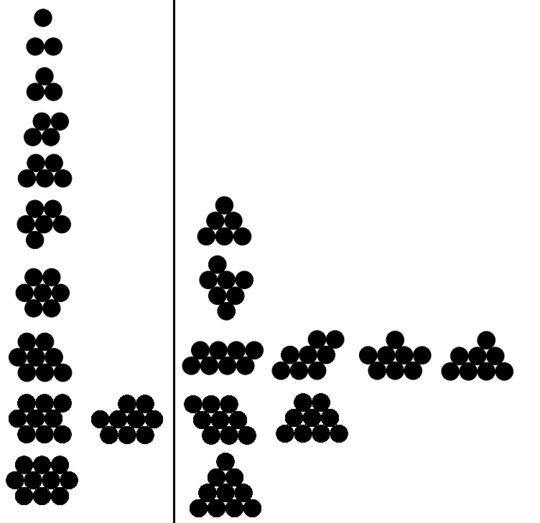
Below I have example valid and invalid outputs for n from 1 to 10 (valid examples only for the first five). The valid examples are on the left; every example on the right has a greater perimeter than the corresponding valid example.
Much thanks to steveverrill for help with writing this challenge. Happy packing!

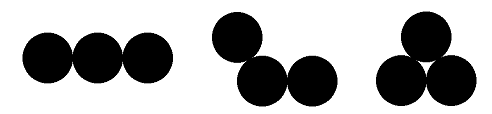
3Waiting on Hexagony, I'm betting. ;D – Addison Crump – 2015-11-22T22:12:55.407
@VoteToClose: I don't think Hexagony has graphical output, but MAN, that'd be awesome! – El'endia Starman – 2015-11-22T23:09:40.083
@El'endiaStarman Well, you could write an SVG to stdout, but I don't think I'm going to... :P – Martin Ender – 2015-11-23T09:57:00.847
1Wow, no-one has thanked me in bold for my comments in the sandbox before. I'm blushing :-D Of course I commented because I liked the challenge, though I'm not sure if i'm going to have time to answer it. – Level River St – 2015-11-23T20:19:07.723
Per my discussion with Reto Koradi on user81655's answer, I think the largest hexagon we will see with sharp corners is sidelength 7d (8 circles.) That's N=169 circles total. You could consider restricting the problem to that number, which would give more chance of getting a correct answer (currently there aren't any) and of being able to check. On the other hand it may be more interesting to leave the problem open up to arbitrary N. – Level River St – 2015-11-24T08:34:11.410
@steveverrill: I think I'll go with the "interesting" choice and require that it work for arbitrary N (within reason, of course). – El'endia Starman – 2015-11-24T08:36:51.330
Update: there is a better solution for N=169 than a perfect hexagon. We leave 2 opposite corners alone, and remove the circles from the remaining 4 corners. We place them on the sides of 5d (6 circles) thus created as near to the middle of the side as possible (as there is an odd number of gaps, there are 2 distinct ways of doing this for each side.) The resulting figure has a perimeter of 41.933 instead of 42. Is it the best possible? probably, I don't know. – Level River St – 2015-11-24T09:22:40.520
This is looking more and more like a code-challenge rather than a code-golf problem! – DavidC – 2015-11-24T16:07:36.560
@DavidCarraher: Haha, yeah, I wasn't totally sure which one to pick before I posted. I don't know if it would be acceptable to change the problem type now, almost 48 hours after it was posted. – El'endia Starman – 2015-11-24T19:01:57.687
I would change it to code-challenge, even at this point, because that will encourage people to pay attention to less than perfect but interesting proposals. It may also encourage people to invest in more imaginative approaches. – DavidC – 2015-11-24T21:17:26.603
@DavidCarraher: I do like that idea. But what should the scoring criteria be? I'm thinking "the first answer to get the best solution for
n=1000". – El'endia Starman – 2015-11-25T00:57:09.493Strangely enough, the solution for
n =1000, or any large number, should be relatively easy: you simply (I think) shrink a circle, with center on 1 hex grid point until the circle holds 1000 hex grid points. You still may have to make minor adjustments because the most efficient solution may lie on a diagonal between two neighboring points. – DavidC – 2015-11-25T01:01:44.920Maybe a popularity contest? You might want to raise the issue of the proper tag in the sandbox. – DavidC – 2015-11-25T01:03:27.680
@DavidCarraher: The Sandbox seems like a strange place to bring that up. The corresponding post has already been edited and deleted. But bringing it up in a separate Meta question also seems a bit strange. Chat would probably be best, but there are few people around (likely because of the upcoming Thanksgiving break). – El'endia Starman – 2015-11-25T01:06:40.390