15
Spherical excess of a triangle
As we all know, the sum of angles of any planar triangle is equal to 180 degrees.
However, for a spherical triangle, the sum of angles is always greater than 180 degrees. The difference between the sum of the spherical triangle angles and 180 degrees is called spherical excess . The task is to compute the spherical excess of a triangle with given vertex coordinates.
Some background
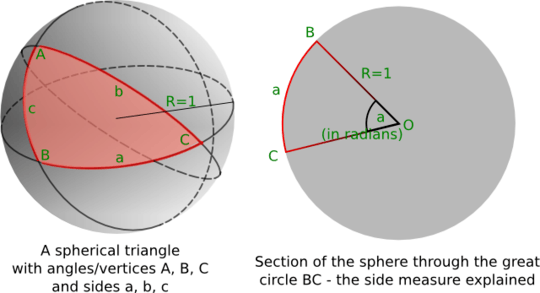
A spherical triangle is a part of the sphere defined by three great circles of the sphere.
Both sides and angles of spherical triangle are measured in the term of angle measure, because each side can be considered as a intersection of the sphere and some planar angle with vertex at the center of the sphere:
Each three distinct great circles define 8 triangles, but we only take proper triangles into consideration, ie. triangles whose angle and side measures satisfy
It's convenient to define vertices of a triangle in terms of geographic coordinate system. To compute the length of an arc of sphere given the longitude λ and latitude Φ of its ends we can use formula:
, where
or more explicitely:
(source: https://en.wikipedia.org/wiki/Haversine_formula)
The two basic formulas that can be used to solve a spherical triangle are:
- the law of cosines:
- the law of sines:
(source: https://en.wikipedia.org/wiki/Spherical_trigonometry#Cosine_rules_and_sine_rules)
Given three sides, it's easy to compute the angles using the cosine rule:
Finally, the spherical excess of a triangle is defined:
What's interesting about the relation between the spherical excess of a triangle and its area:
So on a unit sphere, the excess of a triangle is equal to area of that triangle!
The task
Write a function or a program that will compute spherical excess of a triangle in degrees given the triangle vertices coordinates. The vertex coordinates are provided in terms of geographic coordinate system.
Each vertex should be passed in form [latitude in degrees][N|S][longitude in degrees][E|W]. Longitude and E or W can be skipped when latitude is 90 ie. 90N, 90S, 10N100E, 30S20W are proper vertex descriptions, while 80N or 55S are not.
The latitudes and longitudes are always integer in the test cases.
The answers with error less than one degree will be accepted (as in examples below). The result can be rendered as both real or integer therefore, up to your convenience.
Examples
Input
90N0E
0N0E
0N90E
Output
89.999989
Input
90N
0N0E
0N90E
Output
89.999989
Input
0N0E
0N179E
90N0E
Output
178.998863
Input
10N10E
70N20W
70N40E
Output
11.969793
In all test cases longitude and latitude are integer numbers.
Parsing the vertex coordinates is the part of the task, so a vertex must be passed as single string/literal , it's not allowed to pass 80N20E as four parameters/strings: 80, N, 20, E.
This is guaranteed that vertices are all distinct and neither two of the three vertices make an antipodal points pair.
Scoring
This is code-golf, so the shortest code wins.
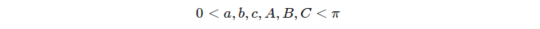
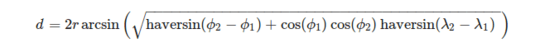
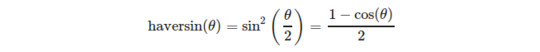
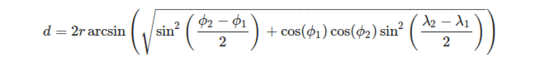
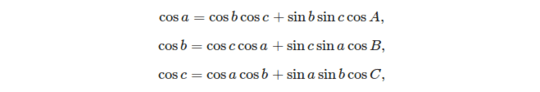
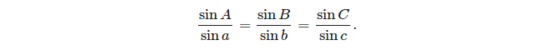
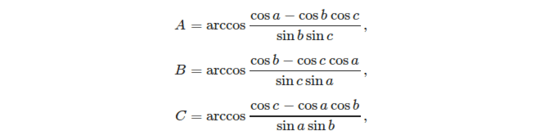
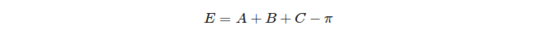
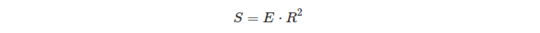
1The correct outputs for the first few test cases are 90 degrees and 179 degrees. I get that you are saying that they don't have to be spot on, but how many decimal places of accuracy are required? – Level River St – 2015-11-14T19:45:40.220
@steveverrill Updated the task. Accuracy of one degree is enough. – pawel.boczarski – 2015-11-14T20:02:09.210
@pawel.boczarski Are latitudes/longitudes always integers? – flawr – 2015-11-14T20:11:34.767
@flawr Yes, I updated the task. – pawel.boczarski – 2015-11-14T20:18:34.973