31
8
Take a look at this chamomile flower:
Pretty, isn't it? Well, what if I told you that this wasn't actually one flower?
A lot of flowers (including sunflowers, chamomiles, daisies and others) actually consist of many very small flowers (the black dots on sunflowers) on a flower head. These miniature flowers are called florets, and they are arranged in a very special way.
Basically, the nth floret's position on a flower head is (in polar coordinates):
where c = 1 (Note that 137.508 degrees = golden angle. You don't have to use this exact precision.)
This causes the florets to be formed in a spiral called Fermat's Spiral. The positioning of the florets also is connected with Fibonnaci numbers, but that's a tale for another time.
So, here's the challenge. Given an integer n as input, calculate the positions of the first n florets and plot them. This is graphical-output, so I do actually want you to display the points in either a window of some sort or outputted as data in some common image format to STDOUT or a file. Other than that, this challenge should be fairly straightforward. It's code-golf, so shortest code wins. GLHF!
Here is a sample picture of what an output might look like:




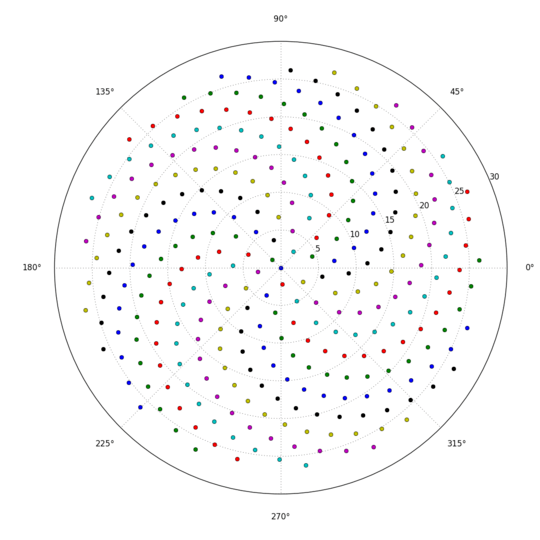
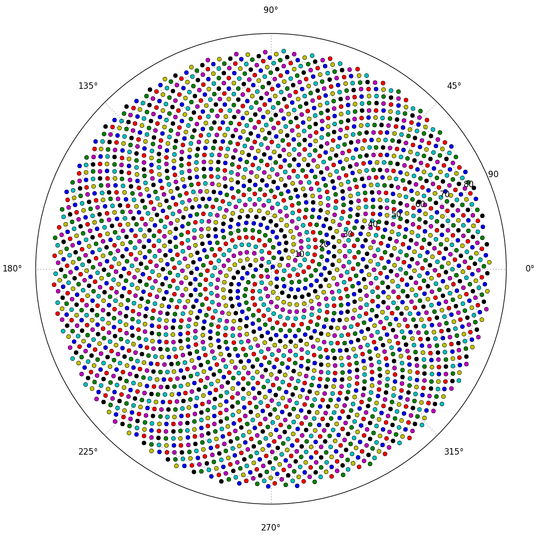


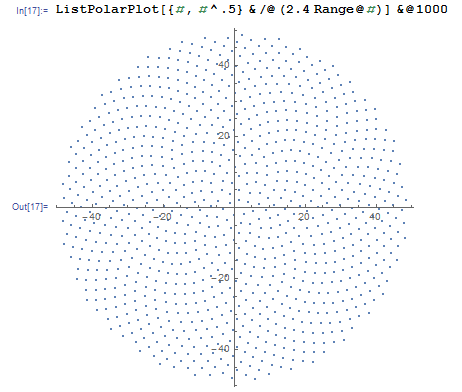
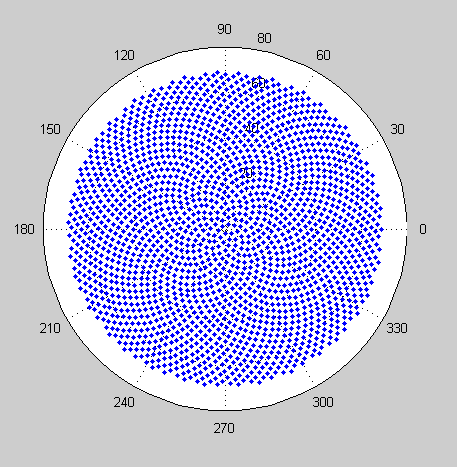

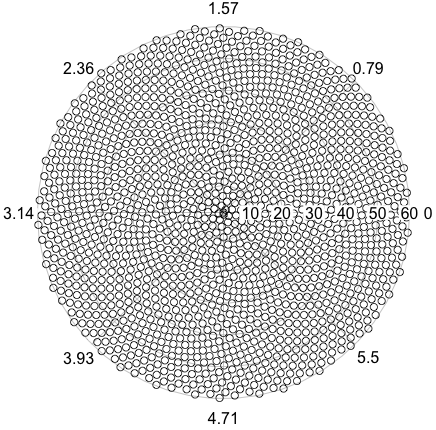
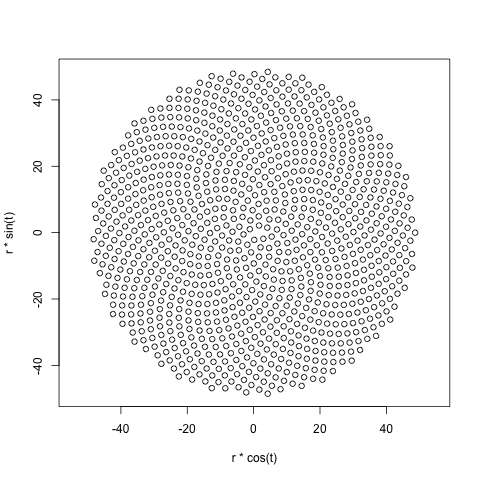
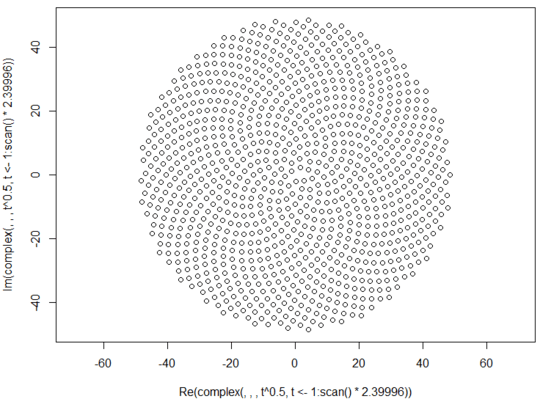

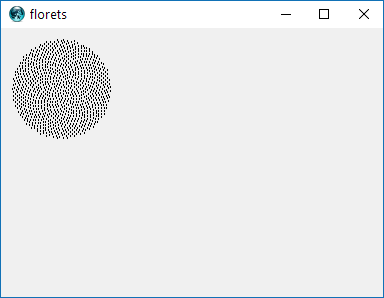
Are we allowed to draw the spiral upside down? – lirtosiast – 2015-10-08T12:58:54.973
1
FWIW many fruits display this pattern, such as the pineapple, agauje, and pinecone. This should not be surprising since fruits develop from flowers. Interestingly some cactus bodies also display this pattern. My favorite is the fractal Romanesco broccoli: https://en.wikipedia.org/wiki/Romanesco_broccoli#/media/File:Romanesco_broccoli_%283%29.jpg
– user151841 – 2015-10-09T16:10:18.2731That's cool! I've seen Romanesco broccoli before; I think it's really cool how they have that fractal pattern. Maybe I could make a challenge about that... – a spaghetto – 2015-10-09T21:04:12.647