Generate the Temple Skyline Sequence

Question

Consider the following process:

1. Take some non-negative integer N.

   e.g. N = 571

2. Express it in binary with no leading zeroes. (Zero itself is the only exception, becoming 0.)

   e.g. 571 = 1000111011 in binary

3. Break apart consecutive runs of ones and zeroes in this binary representation.

   e.g. 1000111011 → 1, 000, 111, 0, 11

4. Sort the runs from longest to shortest.

   e.g. 1, 000, 111, 0, 11 → 000, 111, 11, 1, 0

5. Overwrite all the digits in each run with alternating 1's and 0's, always starting with 1's.

   e.g. 000, 111, 11, 1, 0 → 111, 000, 11, 0, 1

6. Concatenate the result to get a new binary number.

   e.g. 111, 000, 11, 0, 1 → 1110001101 = 909 in decimal

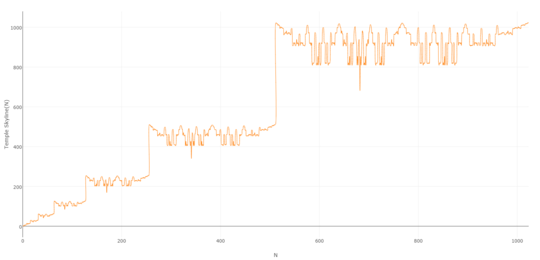
When you plot the values produced by this process you get a pretty neat graph:

And it's hopefully apparent why I'm calling the resulting sequence the Temple Skyline sequence:

Challenge

Write a program or function that takes in a non-negative integer N and prints or returns the corresponding Temple Skyline sequence number. Your input and output should both be in decimal.

e.g. If the input is 571 the output should be 909.

The shortest code in bytes wins.

For reference, here are the terms in the sequence from N = 0 to 20:

0   1
1   1
2   2
3   3
4   6
5   5
6   6
7   7
8   14
9   13
10  10
11  13
12  12
13  13
14  14
15  15
16  30
17  29
18  26
19  25
20  26

Here are the terms from 0 to 1023.

Answer 1

Pyth, 20 19 bytes

ACr.BQ8|is*V_SGH2 1

1 byte saved by Jakube

Test Suite

Uses the fact that after run-length-encoding, the runs are the desired runs in the output.

Lost 3 bytes special casing 0.

Answer 2

CJam, 25 23 22 bytes

ri1e>2be`z($W%a\+ze~2b

Just a bit of run-length encoding. -1 thanks to @MartinBüttner.

Try it online / Test suite.

Explanation

ri        Read n from input as int
1e>       Take max with 1 (special case for n = 0)
2b        Convert n to binary
e`        Run length encode
z         Zip, giving a pair [<counts> <10101.. array>]
($W%      Drop the counts array and sort decending
a\+z      Add it back to the 10101.. array and re-zip
e~        Run length decode
2b        Convert from binary

Answer 3

Pyth - 21 20 bytes

Thanks to @sok for saving me one byte!

is.em%hk2hb_Sr.BQ8 2

Try it here online.

Answer 4

Python 2, 121 bytes 125

121: Thanks to Sp3000 for shaving off 4 bytes!

import re;print int("".join(n*`~i%2`for i,n in enumerate(sorted(map(len,re.split('(1*|0+)',bin(input())[2:])))[::-1])),2)

125

import re;print int("".join("10"[i%2]*n for i,n in enumerate(sorted(map(len,re.split('(1*|0+)',bin(input())[2:])))[::-1])),2)

Answer 5

JavaScript ES6, 110 bytes 113 116 119 120

Saved 3 bytes thanks to @intrepidcoder

Saved 3 bytes thanks to @NinjaBearMonkey

n=>+('0b'+n.toString(2).split(/(0+)/).sort((b,a)=>a.length-b.length).map((l,i)=>l.replace(/./g,i-1&1)).join``)

Straight forward approach. Don't like the length of the sort function but I can't think of a way to golf it.

Answer 6

C++, 535 527 Bytes

(thanks zereges for shaving off some bytes.)

Now that we got rid of those bytes the program is now competetive ;)

#include<iostream>
#include<cmath>
int main(){int I,D;std::cin>>I;while(I>int(pow(2,D))){D++;}int L[99];int X=0;int Z=0;int O=0;for(int i=D-1;i>=0;i--){if( int(pow(2,i))&I){if(Z>0){L[X]=Z;Z=0; X++;}O++;}else{if(O>0){L[X] = O;O=0;X++;}Z++;}}if(Z>0){L[X]=Z;Z=0;X++;}if(O>0){L[X]=O;O=0;X++;}int P=0;bool B = true;int W = D-1;for(int j=0;j<X;j++){int K=0;int mX=0;for(int i=0;i<X;i++){if(L[i]>K){K=L[i];mX=i;}}L[mX]=0;if(B){for(int k=0;k<K;k++){P+=int(pow(2,W));W--;}}else{for(int k=0;k<K;k++){W--;}}B^=1;}std::cout<<P;return 0;}

I'm new to golfing, so please give me some tips in the comments.

Things like "you don't need those brackets" or "use printf" are all helpful, but I also appreciate advice on the logic. Thanks in advance!

For ease of reading, I present the ungolfed version:

#include<iostream>
#include<cmath>
int main()
{
int input,digits;

std::cin>>input;
while(input > int(pow(2,digits))){digits++;}

int list[99];
int index=0;
int zCounter=0;
int oCounter=0;

for(int i=digits;i>0;i--)
{
    if( int(pow(2,i-1))&input)
    {
        if(zCounter>0)
        {
            list[index] = zCounter;
            zCounter=0;
            index++;
        }
        oCounter++;
    }
    else
    {
        if(oCounter>0)
        {
            list[index] = oCounter;
            oCounter=0;
            index++;
        }
        zCounter++;
    }
}
if(zCounter>0)
{
        list[index] = zCounter;
        zCounter=0;
        index++;
}
if(oCounter>0)
{
        list[index] = oCounter;
        oCounter=0;
        index++;
}

int output = 0;
bool ones = true;
int power = digits-1;
for(int j=0;j<index;j++)
{
    int max=0;
    int mIndex=0;
    for(int i=0;i<index;i++)
    {
        if(list[i]>max){max=list[i];mIndex=i;}
    }
    list[mIndex]=0;

    if(ones)
    {
        for(int k=0;k<max;k++)
        {
            output+=int(pow(2,power));
            power--;
        }
    }
    else
    {
        for(int k=0;k<max;k++)
        {
            power--;
        }
    }
    ones^=1;

}
std::cout<<output;
return 0;
}

EDIT golfed version brought down a couple bytes, ungolfed version unchanged

Answer 7

Perl 5.10, 121 101

say oct"0b".join'',map{$|=1-$|;$_=~s/./$|/gr}sort{length$b<=>length$a}(sprintf"%b",shift)=~/(0*|1*)/g

I think the sort part can be shorter.

Edit: -20 bytes, thanks to symbabque!

Answer 8

Haskell, 132 131 bytes

import Data.List
g 0=[]
g n=mod n 2:g(div n 2)
q=[1]:[0]:q
f=foldl((+).(2*))0.concat.zipWith(<*)q.sortOn((-)0.length).group.g.max 1

Usage example:

> map f [0..20]
[1,1,2,3,6,5,6,7,14,13,10,13,12,13,14,15,30,29,26,25,26]

How it works:

                 max 1         -- fix n=0: f(0) is the same as f(1)
               g               -- turn into binary, i.e. list of 0s and 1s
            group              -- group sequences of equal elements
         sortOn((-)0.length)   -- sort groups on negative length
      zipWith(<*)q             -- map each element in a group to constant 1 or 0 by turns
   concat                      -- flatten all groups into a single list
foldl((+).(2*))0               -- convert back to decimal

Answer 9

J - 30 bytes

Function taking integer on right. Correctly handles 0.

(\:~#2|#\)@(#;.1~1,2~:/\])&.#:

• #: - Take the binary representation.
• 1,2~:/\] - Between each digit, report True if they are different. Prepend a True so that the list has True at the start of each "run".
• (#;.1~...) - Using the boolean vector above, take the length of each run.
• \:~ - Sort these lengths from longest to shortest.
• 2|#\ - Take a list of alternating 1 0 1 0 ... as long as the list of lengths.
• (...#...) - For each number on the left (sorted lengths), take as many of the corresponding item on the right (alternating 1's and 0's)
• &. - Convert this new binary representation back to a number.

Examples:

   (\:~#2|#\)@(#;.1~1,2~:/\])&.#: 571
909
   i.21   NB. zero to twenty
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
   (\:~#2|#\)@(#;.1~1,2~:/\])&.#: every i.21   NB. apply separately to every number
1 1 2 3 6 5 6 7 14 13 10 13 12 13 14 15 30 29 26 25 26

Answer 10

Python 3, 146 136 bytes

import re;print(int(''.join(len(j)*'01'[i%2<1]for i,j in enumerate(sorted(re.findall('1+|0+',bin(int(input()))[2:]),key=len)[::-1])),2))

Answer 11

Mathematica, 83 bytes

Flatten[0#+(d=1-d)&/@SortBy[d=0;Split[#~IntegerDigits~2],-Length@#&]]~FromDigits~2&

This defines an unnamed function.

Answer 12

Ruby, 107 104 102 bytes

(saved 3 bytes thanks to nimi)

Not going to beat the likes of CJam, but I got it pretty small for a sane language.

p gets.to_i.to_s(2).scan(/((.)\2*)/).map{|e|e[i=0].size}.sort.reverse.map{|e|"#{i=1-i}"*e}.join.to_i 2

Answer 13

Java 8, 179 176 bytes

(x)->{int g[]=new int[32],h=0,i=highestOneBit(x);g[0]=1;while(i>1)g[((x&i)>0)^((x&(i>>=1))>0)?++h:h]++;sort(g);for(i=32,h=0;g[--i]>0;)while(g[i]-->0)h=h<<1|i%2;return x<1?1:h;}

I used two static imports: java.util.Integer.highestOneBit and java.util.Arrays.sort.

For readability, here's the code ungolfed:

java.util.function.ToIntFunction<Integer> f = (x) -> {
  int g[] = new int[32], h = 0, i = java.util.Integer.highestOneBit(x);
  g[0] = 1;
  while (i > 1) {
    g[((x & i) > 0) ^ ((x & (i >>= 1)) > 0) ? ++h : h]++;
  }
  java.util.Arrays.sort(g);
  for (i = 32, h = 0; g[--i] > 0;) {
    while (g[i]-- > 0) {
      h = h << 1 | i % 2;
    }
  }
  return x < 1 ? 1 : h; // handle zero
};

Answer 14

Python 2, 170 bytes

def t(n):
  from itertools import groupby;lst=sorted([''.join(g) for n,g in groupby(bin(n)[2:])],key=len)[::-1];s=''
  for i in lst:s+=str(i)
  return int(s,2)