202
46
Believe it or not, we do not yet have a code golf challenge for a simple primality test. While it may not be the most interesting challenge, particularly for "usual" languages, it can be nontrivial in many languages.
Rosetta code features lists by language of idiomatic approaches to primality testing, one using the Miller-Rabin test specifically and another using trial division. However, "most idiomatic" often does not coincide with "shortest." In an effort to make Programming Puzzles and Code Golf the go-to site for code golf, this challenge seeks to compile a catalog of the shortest approach in every language, similar to "Hello, World!" and Golf you a quine for great good!.
Furthermore, the capability of implementing a primality test is part of our definition of programming language, so this challenge will also serve as a directory of proven programming languages.
Task
Write a full program that, given a strictly positive integer n as input, determines whether n is prime and prints a truthy or falsy value accordingly.
For the purpose of this challenge, an integer is prime if it has exactly two strictly positive divisors. Note that this excludes 1, who is its only strictly positive divisor.
Your algorithm must be deterministic (i.e., produce the correct output with probability 1) and should, in theory, work for arbitrarily large integers. In practice, you may assume that the input can be stored in your data type, as long as the program works for integers from 1 to 255.
Input
If your language is able to read from STDIN, accept command-line arguments or any other alternative form of user input, you can read the integer as its decimal representation, unary representation (using a character of your choice), byte array (big or little endian) or single byte (if this is your languages largest data type).
If (and only if) your language is unable to accept any kind of user input, you may hardcode the input in your program.
In this case, the hardcoded integer must be easily exchangeable. In particular, it may appear only in a single place in the entire program.
For scoring purposes, submit the program that corresponds to the input 1.
Output
Output has to be written to STDOUT or closest alternative.
If possible, output should consist solely of a truthy or falsy value (or a string representation thereof), optionally followed by a single newline.
The only exception to this rule is constant output of your language's interpreter that cannot be suppressed, such as a greeting, ANSI color codes or indentation.
Additional rules
This is not about finding the language with the shortest approach for prime testing, this is about finding the shortest approach in every language. Therefore, no answer will be marked as accepted.
Submissions in most languages will be scored in bytes in an appropriate preexisting encoding, usually (but not necessarily) UTF-8.
The language Piet, for example, will be scored in codels, which is the natural choice for this language.
Some languages, like Folders, are a bit tricky to score. If in doubt, please ask on Meta.
Unlike our usual rules, feel free to use a language (or language version) even if it's newer than this challenge. If anyone wants to abuse this by creating a language where the empty program performs a primality test, then congrats for paving the way for a very boring answer.
Note that there must be an interpreter so the submission can be tested. It is allowed (and even encouraged) to write this interpreter yourself for a previously unimplemented language.
If your language of choice is a trivial variant of another (potentially more popular) language which already has an answer (think BASIC or SQL dialects, Unix shells or trivial Brainfuck derivatives like Headsecks or Unary), consider adding a note to the existing answer that the same or a very similar solution is also the shortest in the other language.
Built-in functions for testing primality are allowed. This challenge is meant to catalog the shortest possible solution in each language, so if it's shorter to use a built-in in your language, go for it.
Unless they have been overruled earlier, all standard code-golf rules apply, including the http://meta.codegolf.stackexchange.com/q/1061.
As a side note, please don't downvote boring (but valid) answers in languages where there is not much to golf; these are still useful to this question as it tries to compile a catalog as complete as possible. However, do primarily upvote answers in languages where the author actually had to put effort into golfing the code.
Catalog
The Stack Snippet at the bottom of this post generates the catalog from the answers a) as a list of shortest solution per language and b) as an overall leaderboard.
To make sure that your answer shows up, please start your answer with a headline, using the following Markdown template:
## Language Name, N bytes
where N is the size of your submission. If you improve your score, you can keep old scores in the headline, by striking them through. For instance:
## Ruby, <s>104</s> <s>101</s> 96 bytes
If there you want to include multiple numbers in your header (e.g. because your score is the sum of two files or you want to list interpreter flag penalties separately), make sure that the actual score is the last number in the header:
## Perl, 43 + 2 (-p flag) = 45 bytes
You can also make the language name a link which will then show up in the snippet:
## [><>](http://esolangs.org/wiki/Fish), 121 bytes
<style>body { text-align: left !important} #answer-list { padding: 10px; width: 290px; float: left; } #language-list { padding: 10px; width: 290px; float: left; } table thead { font-weight: bold; } table td { padding: 5px; }</style><script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script> <link rel="stylesheet" type="text/css" href="//cdn.sstatic.net/codegolf/all.css?v=83c949450c8b"> <div id="language-list"> <h2>Shortest Solution by Language</h2> <table class="language-list"> <thead> <tr><td>Language</td><td>User</td><td>Score</td></tr> </thead> <tbody id="languages"> </tbody> </table> </div> <div id="answer-list"> <h2>Leaderboard</h2> <table class="answer-list"> <thead> <tr><td></td><td>Author</td><td>Language</td><td>Size</td></tr> </thead> <tbody id="answers"> </tbody> </table> </div> <table style="display: none"> <tbody id="answer-template"> <tr><td>{{PLACE}}</td><td>{{NAME}}</td><td>{{LANGUAGE}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr> </tbody> </table> <table style="display: none"> <tbody id="language-template"> <tr><td>{{LANGUAGE}}</td><td>{{NAME}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr> </tbody> </table><script>var QUESTION_ID = 57617; var ANSWER_FILTER = "!t)IWYnsLAZle2tQ3KqrVveCRJfxcRLe"; var COMMENT_FILTER = "!)Q2B_A2kjfAiU78X(md6BoYk"; var OVERRIDE_USER = 12012; var answers = [], answers_hash, answer_ids, answer_page = 1, more_answers = true, comment_page; function answersUrl(index) { return "https://api.stackexchange.com/2.2/questions/" + QUESTION_ID + "/answers?page=" + index + "&pagesize=100&order=desc&sort=creation&site=codegolf&filter=" + ANSWER_FILTER; } function commentUrl(index, answers) { return "https://api.stackexchange.com/2.2/answers/" + answers.join(';') + "/comments?page=" + index + "&pagesize=100&order=desc&sort=creation&site=codegolf&filter=" + COMMENT_FILTER; } function getAnswers() { jQuery.ajax({ url: answersUrl(answer_page++), method: "get", dataType: "jsonp", crossDomain: true, success: function (data) { answers.push.apply(answers, data.items); answers_hash = []; answer_ids = []; data.items.forEach(function(a) { a.comments = []; var id = +a.share_link.match(/\d+/); answer_ids.push(id); answers_hash[id] = a; }); if (!data.has_more) more_answers = false; comment_page = 1; getComments(); } }); } function getComments() { jQuery.ajax({ url: commentUrl(comment_page++, answer_ids), method: "get", dataType: "jsonp", crossDomain: true, success: function (data) { data.items.forEach(function(c) { if (c.owner.user_id === OVERRIDE_USER) answers_hash[c.post_id].comments.push(c); }); if (data.has_more) getComments(); else if (more_answers) getAnswers(); else process(); } }); } getAnswers(); var SCORE_REG = /<h\d>\s*([^\n,<]*(?:<(?:[^\n>]*>[^\n<]*<\/[^\n>]*>)[^\n,<]*)*),.*?(\d+)(?=[^\n\d<>]*(?:<(?:s>[^\n<>]*<\/s>|[^\n<>]+>)[^\n\d<>]*)*<\/h\d>)/; var OVERRIDE_REG = /^Override\s*header:\s*/i; function getAuthorName(a) { return a.owner.display_name; } function process() { var valid = []; answers.forEach(function(a) { var body = a.body; a.comments.forEach(function(c) { if(OVERRIDE_REG.test(c.body)) body = '<h1>' + c.body.replace(OVERRIDE_REG, '') + '</h1>'; }); var match = body.match(SCORE_REG); if (match) valid.push({ user: getAuthorName(a), size: +match[2], language: match[1], link: a.share_link, }); else console.log(body); }); valid.sort(function (a, b) { var aB = a.size, bB = b.size; return aB - bB }); var languages = {}; var place = 1; var lastSize = null; var lastPlace = 1; valid.forEach(function (a) { if (a.size != lastSize) lastPlace = place; lastSize = a.size; ++place; var answer = jQuery("#answer-template").html(); answer = answer.replace("{{PLACE}}", lastPlace + ".") .replace("{{NAME}}", a.user) .replace("{{LANGUAGE}}", a.language) .replace("{{SIZE}}", a.size) .replace("{{LINK}}", a.link); answer = jQuery(answer); jQuery("#answers").append(answer); var lang = a.language; lang = jQuery('<a>'+lang+'</a>').text(); languages[lang] = languages[lang] || {lang: a.language, lang_raw: lang.toLowerCase(), user: a.user, size: a.size, link: a.link}; }); var langs = []; for (var lang in languages) if (languages.hasOwnProperty(lang)) langs.push(languages[lang]); langs.sort(function (a, b) { if (a.lang_raw > b.lang_raw) return 1; if (a.lang_raw < b.lang_raw) return -1; return 0; }); for (var i = 0; i < langs.length; ++i) { var language = jQuery("#language-template").html(); var lang = langs[i]; language = language.replace("{{LANGUAGE}}", lang.lang) .replace("{{NAME}}", lang.user) .replace("{{SIZE}}", lang.size) .replace("{{LINK}}", lang.link); language = jQuery(language); jQuery("#languages").append(language); } }</script>






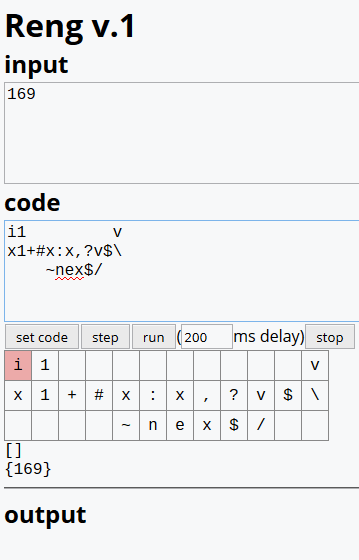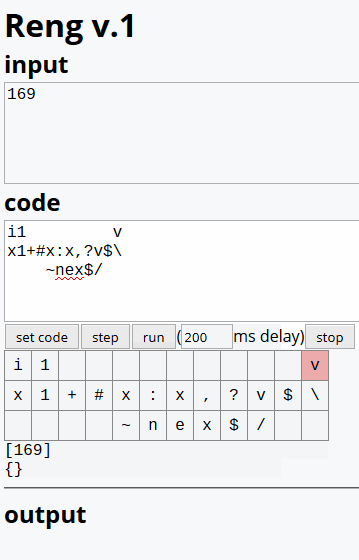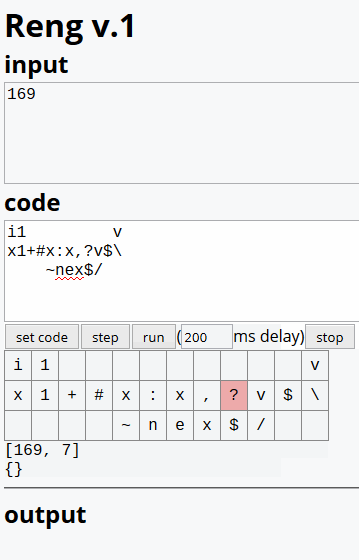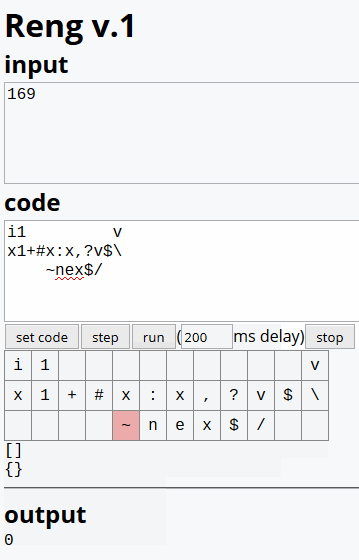
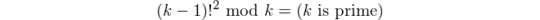
Can I take inputs as negative numbers, where abs(input) would be the number I am testing? – Stan Strum – 2017-09-06T03:40:28.880
No, the input is a strictly positive integer. – Dennis – 2017-09-06T03:44:53.347
1
Is there a reason for the full program requirement, rather than allowing the full range of default input types? E.g. answering with a function that takes its input as an argument, is currently disallowed? https://codegolf.meta.stackexchange.com/questions/2447/default-for-code-golf-input-output-methods
– Lyndon White – 2017-12-12T06:21:55.6632
@LyndonWhite This was intended as a catalog (like “Hello, World!”) of primality tests, so a unified submission format seemed preferable. It's one of two decisions about this challenge that I regret, the other being only allowing deterministic primality tests.
– Dennis – 2017-12-12T12:51:06.730Could a case be made for locking this challenge and posting a new, less restrictive one? – Shaggy – 2018-06-25T12:59:32.587
1@Shaggy Seems like a question for meta. – Dennis – 2018-06-25T13:44:07.693
1Yeah, that's what I was thinking. I'll let you do the honours, seeing as it's your challenge. – Shaggy – 2018-06-25T13:45:55.260
Is it ok if an answer falsely says
1is prime, or would this disqualify and answer? – The Matt – 2020-02-07T22:35:37.007