Cut a silicon wafer into dies

Question

When manufacturing chips, circular silicon wafers are cut into dies of needed size:

The goal of this challenge is maximizing the number of whole dies that can be cut from a wafer of a given diameter.

The machine puts the wafer into an angular compartment:

_____________________
|     xxxxxx
|  xxxxxxxxxxxx
| xxxxxxxxxxxxxx
|xxxxxxxxxxxxxxxx
|xxxxxxxxxxxxxxxx
| xxxxxxxxxxxxxx
|  xxxxxxxxxxxx
|     xxxxxx     (this ascii art is meant to be a perfect circle)

It measures a distance dx from the left edge, and makes a vertical cut. Then it makes the needed number of additional vertical cuts, with spacing of the needed width. It makes the horizontal cuts in the same way: first one at a distance dy, and then with spacing of height.

The material remains perfectly still during the cutting: it's not allowed to move some slices of material before making the perpendicular cuts.

The machine has a stepper motor that works at absolute accuracy but can only go integer-sized distances.

Make a program or a subroutine that gets (or reads) the following parameters:

• Wafer diameter
• Die width
• Die height

and outputs (or prints)

• dx - horizontal starting position
• dy - vertical starting position

such that the number of rectangular dies is maximal.

Some fine points:

• If a corner of a die lies exactly on the circumference of the circle, the die is considered usable (rectangular)
• No edge cases: you can assume that the wafer's diameter is even; at least one die can be cut out; also make other reasonable assumptions
• All sizes are integer numbers of millimeters; maximum wafer diameter is 450

Shortest code wins!

P.S. The code must finish running in a reasonable amount of time, e.g. over a weekend (2 days) - for wafer diameter equal to 300.

P.P.S. If there are several different output values that are optimal, the code must output one of them - no need to output all of them!

Test cases:

Wafer diameter 8, die size 2 x 2 => dx = 0, dy = 1 (6 dies)
Wafer diameter 20, die size 5 x 4 => dx = 1, dy = 2 (10 dies)
Wafer diameter 100, die size 12 x 12 => dx = 9, dy = 3 (41 dies)
Wafer diameter 300, die size 11 x 11 => dx = 7, dy = 7 (540 dies) - a realistic example
Wafer diameter 340, die size 15 x 8 => dx = 5, dy = 2 (700 dies) - a Pythagorean triple
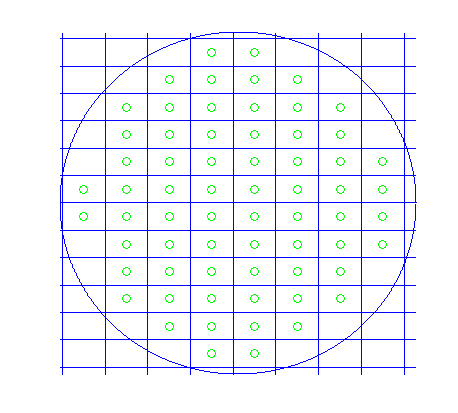
Wafer diameter 300, die size 36 x 24 => dx = 2, dy = 6 (66 dies) - full-frame sensors

Here is a visualization of the last test case:

Answer 1

Java, 242

This is a method that takes the three input parameters and returns a string containing optimal values for dx and dy.

String k(int d,int w,int h){int m=0,f=0,g=0,r=d/2,s=r*r+1,a,b,p=-1;while(++p<w)for(int q=-1;++q<h;)for(int x=p-r,c=0;(a=x+w)<r;x=a)for(int y=q-r;(b=y+h)<r;y=b)if(x*x+y*y<s&&a*a+b*b<s&&x*x+b*b<s&&a*a+y*y<s&&++c>m){m=c;f=p;g=q;}return f+" "+g;}

Ungolfed:

String k(int diameter, int width, int height) {
    int
        maxDieCount = 0,
        bestDx = 0,
        bestDy = 0,
        radius = diameter / 2,
        radiusSquared = radius * radius;
    for (int dx = 0; dx < width; ++dx) {
        for (int dy = 0; dy < height; ++dy) {
            int dieCount = 0;
            for (int x1 = dx - radius; x1 + width < radius; x1 += width) {
                int x2 = x1 + width;
                for (int y1 = dy - radius; y1 + height < radius; y1 += height) {
                    int y2 = y1 + height;
                    if (    x1 * x1 + y1 * y1 <= radiusSquared &&
                            x2 * x2 + y2 * y2 <= radiusSquared &&
                            x1 * x1 + y2 * y2 <= radiusSquared &&
                            x2 * x2 + y1 * y1 <= radiusSquared )
                        ++dieCount;
                }
            }
            if (dieCount > maxDieCount) {
                maxDieCount = dieCount;
                bestDx = dx;
                bestDy = dy;
            }
        }
    }
    return bestDx + " " + bestDy;
}

Pretty straightforward bruteforce approach - try every dx in [0, width) and every dy in [0, height), then loop through every rectangle in the resulting grid and check if all four corners are inside the circle (using basic pythagorean relations), count the number of such rectangles, and return the first dx and dy that produced the highest count for the given configuration.

Test with: (assuming both methods are placed in a class named CG52148)

public static void main(String[] args) {

    CG52148 o = new CG52148();
    System.out.println("8\t2\t2\t=> " + o.k(8, 2, 2));
    System.out.println("20\t5\t4\t=> " + o.k(20, 5, 4));
    System.out.println("100\t12\t12\t=> " + o.k(100, 12, 12));
    System.out.println("300\t11\t11\t=> " + o.k(300, 11, 11));
    System.out.println("340\t15\t8\t=> " + o.k(340, 15, 8));
    System.out.println("300\t36\t24\t=> " + o.k(300, 36, 24));

}

The third test case produces 0 8 rather than 9 3, but they are both valid, equally optimal, and are both found by my algorithm.

Answer 2

Python 2.7, 317

Here is my solution. Could be golfed a bit more, I think - but I like the solving better than the golfing. Suggestions are welcome.

I solve it using brute force, iterating over all dx and dy and then counting by column. It all runs pretty fast (<0,05 sec. on my Mac).

Code:

import math as m
def D(d,w,h):
 r=d/2
 s=[0,0,0]
 for dx in range(0,w):
  for dy in range(0,h):
   t=0
   for c in range(1,int(d/w)+1):
    l=r-dx-(c-1)*w
    if l<w/2:
     l-=w
    if abs(l)<=r:
     f=r*m.sin(m.acos(1.0*l/r));t+=int((2.0*f-(dy+m.ceil((r-dy-f)/h)*h+f-r))/h)
   if t>s[0]:
    s=[t,dx,dy]
 return s

A main to test and profile the given cases:

def runTestcases():
    for d,w,h in [[8,2,2],[20,5,4],[100,12,12],[300,11,11],[340,15,8],[300,36,24]]:
        S=D(d,w,h)
        print "Wafer diameter {}, die size {} x {} => dx = {}, dy = {} ({} dies)".format(d,w,h,S[1],S[2],S[0])

def main():
    import cProfile
    cProfile.run("runTestcases()")

if __name__ == "__main__":
    main()

And its output:

Wafer diameter 8, die size 2 x 2 => dx = 0, dy = 1 (6 dies)
Wafer diameter 20, die size 5 x 4 => dx = 1, dy = 2 (10 dies)
Wafer diameter 100, die size 12 x 12 => dx = 0, dy = 8 (41 dies)
Wafer diameter 300, die size 11 x 11 => dx = 7, dy = 7 (540 dies)
Wafer diameter 340, die size 15 x 8 => dx = 5, dy = 2 (700 dies)
Wafer diameter 300, die size 36 x 24 => dx = 2, dy = 6 (66 dies)
         55354 function calls in 0.049 seconds