10
1
[This is a partner question to Calculate a probability exactly ]
This task is about writing code to compute a probability exactly and quickly. The output should be a precise probability written as a fraction in its most reduced form. That is it should never output 4/8 but rather 1/2.
For some positive integer n, consider a uniformly random string of 1s and -1s of length n and call it A. Now concatenate to A its first value. That is A[1] = A[n+1] if indexing from 1. A now has length n+1. Now also consider a second random string of length n whose first n values are -1, 0, or 1 with probability 1/4,1/2, 1/4 each and call it B.
Now consider the inner product of A[1,...,n] and B and the inner product of A[2,...,n+1] and B.
For example, consider n=3. Possible values for A and B could be A = [-1,1,1,-1] and B=[0,1,-1]. In this case the two inner products are 0 and 2.
Your code must output the probability that both inner products are zero.
Copying the table produced by Martin Büttner we have the following sample results.
n P(n)
1 1/2
2 3/8
3 7/32
4 89/512
5 269/2048
6 903/8192
7 3035/32768
8 169801/2097152
Languages and libraries
You can use any freely available language and libraries you like. I must be able to run your code so please include a full explanation for how to run/compile your code in linux if at all possible.
The task
Your code must start with n=1 and give the correct output for each increasing n on a separate line. It should stop after 10 seconds.
The score
The score is simply the highest n reached before your code stops after 10 seconds when run on my computer. If there is a tie, the winner be the one to get to the highest score quickest.
Table of entries
n = 64in Python. Version 1 by Mitch Schwartzn = 106in Python. Version June 11 2015 by Mitch Schwartzn = 151in C++. Port of Mitch Schwartz's answer by kirbyfan64sosn = 165in Python. Version June 11 2015 the "pruning" version by Mitch Schwartz withN_MAX = 165.n = 945in Python by Min_25 using an exact formula. Amazing!n = 1228in Python by Mitch Schwartz using another exact formula (based on Min_25's previous answer).n = 2761in Python by Mitch Schwartz using a faster implementation of the same exact formula.n = 3250in Python using Pypy by Mitch Schwartz using the same implementation. This score needspypy MitchSchwartz-faster.py |tailto avoid console scrolling overhead.
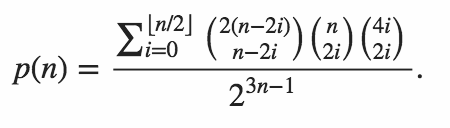
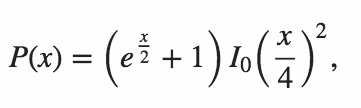
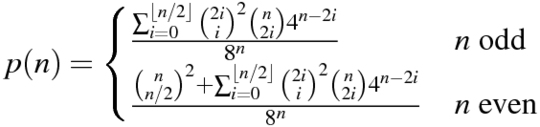
I wonder if a numpy solution would run faster than Boost C++? – qwr – 2015-06-10T21:45:04.770
@qwr I think numpy, numba and cython would all be interesting as they keep within the Python family. – None – 2015-06-11T07:57:41.387
2I'd love to see more of these fastest-code problems – qwr – 2015-06-11T18:09:22.170
@qwr it's my favourite sort of question... Thank you! The challenge is to find one that doesn't just involve coding exactly the same algorithm in the lowest level language you can find. – None – 2015-06-11T18:10:40.707
Are you writing the results to the console or to a file? Using pypy and writing to a file seems the fastest for me. The console slows the process considerably. – gnibbler – 2015-06-15T21:13:13.400
@gnibbler Thank you! I updated the fastest score following your suggestion. I did find that pypy slowed down the dynamic programming approaches however. – None – 2015-06-16T05:58:27.097