20
Background
The birthday paradox is a popular problem in probability theory which defies (most people's) mathematical intuition. The problem statement is:
Given N people, what is the probability that at least two of them have the same birthday (disregarding the year).
The problem is usually simplified by ignoring leap days entirely. In this case, the answer for N = 23 is P(23) ≈ 0.5072972 (as a common example). The linked Wikipedia article explains how to arrive at this probability. Alternatively, this Numberphile video does a really good job.
However, for this challenge we want to do it right and don't ignore leap years. This is slightly more complicated, since now the 29th of February needs to be added, but this particular birthday is less likely than all the others.
We'll also use the full leap year rules:
- If a year is divisible by 400 it's a leap year.
- Else, if a year is divisible by 100 it's not a leap year.
- Else, if a year is divisible by 4 it's a leap year.
- Else, it's not a leap year.
Confused? It means that the years 1700, 1800, 1900, 2100, 2200, 2300 are not leap years, but 1600, 2000, 2400 are (as well as any other year divisible by 4). This calendar repeats every 400 years, and we will assume a uniform distribution of birthdays over those 400 years.
The corrected result for N = 23 is now P(23) ≈ 0.5068761.
The Challenge
Given an integer 1 ≤ N < 100, determine the probability that among N people at least two have the same birthday under consideration of the leap year rules. The result should be a floating-point or fixed-point number, accurate to at least 6 decimal places. It is acceptable to truncate trailing zeroes.
You may write a program or function, taking input via STDIN (or closest alternative), command-line argument or function argument and output the result via STDOUT (or closest alternative), function return value or function (out) parameter.
Your solution must be able to produce output for all 99 inputs in a matter of seconds. This is mainly to rule out Monte Carlo methods with tons of samples, so if you're using a principally fast and exact algorithm in an excessively slow esoteric language, I'm willing to give leeway on this rule.
Test Cases
Here is the full table of results:
1 => 0.000000
2 => 0.002737
3 => 0.008195
4 => 0.016337
5 => 0.027104
6 => 0.040416
7 => 0.056171
8 => 0.074251
9 => 0.094518
10 => 0.116818
11 => 0.140987
12 => 0.166844
13 => 0.194203
14 => 0.222869
15 => 0.252642
16 => 0.283319
17 => 0.314698
18 => 0.346578
19 => 0.378764
20 => 0.411063
21 => 0.443296
22 => 0.475287
23 => 0.506876
24 => 0.537913
25 => 0.568260
26 => 0.597796
27 => 0.626412
28 => 0.654014
29 => 0.680524
30 => 0.705877
31 => 0.730022
32 => 0.752924
33 => 0.774560
34 => 0.794917
35 => 0.813998
36 => 0.831812
37 => 0.848381
38 => 0.863732
39 => 0.877901
40 => 0.890932
41 => 0.902870
42 => 0.913767
43 => 0.923678
44 => 0.932658
45 => 0.940766
46 => 0.948060
47 => 0.954598
48 => 0.960437
49 => 0.965634
50 => 0.970242
51 => 0.974313
52 => 0.977898
53 => 0.981043
54 => 0.983792
55 => 0.986187
56 => 0.988266
57 => 0.990064
58 => 0.991614
59 => 0.992945
60 => 0.994084
61 => 0.995055
62 => 0.995880
63 => 0.996579
64 => 0.997169
65 => 0.997665
66 => 0.998080
67 => 0.998427
68 => 0.998715
69 => 0.998954
70 => 0.999152
71 => 0.999314
72 => 0.999447
73 => 0.999556
74 => 0.999645
75 => 0.999717
76 => 0.999775
77 => 0.999822
78 => 0.999859
79 => 0.999889
80 => 0.999913
81 => 0.999932
82 => 0.999947
83 => 0.999959
84 => 0.999968
85 => 0.999976
86 => 0.999981
87 => 0.999986
88 => 0.999989
89 => 0.999992
90 => 0.999994
91 => 0.999995
92 => 0.999996
93 => 0.999997
94 => 0.999998
95 => 0.999999
96 => 0.999999
97 => 0.999999
98 => 0.999999
99 => 1.000000
(Of course, P(99) is only 1.0 due to rounding. The probability won't reach exactly 1.0 until P(367).)
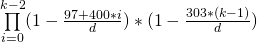
7>
1@PeterTaylor Yes, assume uniform distribution over the full 400 year cycle. I never said the set of N people was alive at the same time. ;) – Martin Ender – 2015-04-24T15:22:07.850