Optimal Games of Tic Tac Torus

Question

This challenge is about the game Tic Tac Toe, but it's played on a torus.

How to play

To create the necessary game board, you start out with a regular Tic Tac Toe game board. First fold it into a cylinder by joining the left and the right edge. Then fold it into torus by joining the top and the bottom edge. Here's a simple visualization of such a game board with a few moves played (Sick Paint skills!).

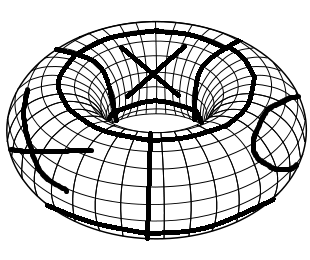
The rules of Tic Tac Toe on a torus are the same as regular Tic Tac Toe. Each Player place alternating Xs and Os. The first one with 3 same symbols in a row, a column or a in a diagonal wins.

Since a torus is quite hard to visualize, we simply project the board back onto a paper. Now we can play the game as regular Tic Tac Toe. The only difference is, that you can also win with 3 same symbols in a broken diagonal. For instance Player 1 (X) wins the following board. You can see this easily by changing the view on the torus a little bit.

If your interested, you can play Tic Tac Toe on a Torus at Torus Games. There's a Windows, Mac and Android version.

Optimal Games

In this challenge were interested in optimal games. An optimal game is a game, where both players play an optimal strategy. On a regular Tic Tac Toe board optimal games always end in a draw. Fascinatingly on a torus board always the first player wins. In fact a game on a torus board can never end in a draw (also if the players play not optimal).

The optimal strategy is really easy:

• If you can win by placing your symbol, do it.
• Otherwise if your opponent has two symbols in one row/column/điagonal, try to block him. Otherwise, do what you want.
• Otherwise do what you want.

Every optimal game consists of exactly 7 moves and these moves can be described in the following way:

1. Player 1 places a X anywhere on the board (9 choices)
2. Player 2 places an O anywhere on the board (8 choices)
3. Player 1 places a X anywhere on the board (7 choices)
4. Player 2's move may be forced (1 choice), if not, he places the O anywhere (6 choices)
5. Player 1's move is forced (1 choice)
6. Player 2 is caught in a fork (Player 1 can win in two different ways), so Player 2 has to block Player 1 in one way (2 choices)
7. Player 1 places the his last move and wins (1 choice)

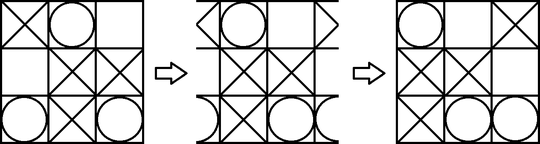
There are 9*8*1*6*1*2*1 + 9*8*6*1*1*2*1 = 1728 different optimal games on our projected board. Here you can see one typical optimal game:

If we label each cell of the board with the digits 0-8, we can describe this game by the digits 3518207. First a X is places in the cell 3 (middle row, left column), than an O in cell 5 (middle row, right column), than a X in cell 1 (upper row, middle column), ...

Using this digit notation we automatically generated an order. Now we can sort all of the 1728 optimal games and we get the list:

Game 0000: 0123845
Game 0001: 0123854
Game 0002: 0124735
Game 0003: 0124753
Game 0004: 0125634
   ...
Game 0674: 3518207
   ...
Game 1000: 5167423
Game 1001: 5167432
Game 1002: 5168304
   ...
Game 1726: 8765034
Game 1727: 8765043

Challenge

This list is part of your job. You will receive one number k between 0 and 1727 and you have to return the kth game in digit notation of that sorted list.

Write a function or a program, that receives the number k (integer) computes the correspondent game. You can read the input via STDIN, command-line argument, prompt or function argument and print the result (7 digits) in a readable format (e.g. 0123845 or [0, 1, 2, 3, 8, 4, 5]) or return it using an string (human readable format) or an integer (containing all digits in base 10), or in any array/list format.

The challenge type is code-golf. Therefore the shortest code wins.

Answer 1

JavaScript (ES6), 266 308 317 334 341

A function returning a string. Edit Found an arithmetic solution for function M (at last!)

F=(n,x=[],M=(a,b,t=-a-b)=>(a-b)%3?a<3&b<3?3+t:a>5&b>5?21+t:12+t:9+t+a%3*3)=>
[for(a of z='012345678')for(b of z)for(c of z)for(d of z) 
a-b&&c-a&&c-b&&(b-(y=M(a,c))?d==y:d-a&&d-b&&d-c)&&(
f=M(c,e=M(b,d)),g=M(a,e),g<f?[f,g]=[g,f]:0,r=a+b+c+d+e,x.push(r+f+g,r+g+f))]
&&x[n]

Very naive , it can be shortened in many ways. It simply enumerates all the possible legal values and returns what find at place n. The M function returns the position in between two cells, that is the mandatory move to block an opposite player.

More readable

F=(n,x=[],
  M=(a,b,t=-a-b)=>(a-b)%3? 
     a<3&b<3?
       3+t // first row
       :a>5&b>5?
          21+t // last row
          :12+t // middle row and diags
     :9+t+a%3*3 // columns
  )=>
  [for(a of z='012345678') // enumerate the first 4 moves
     for(b of z)
       for(c of z)
         for(d of z) 
           a-b&&c-a&&c-b // avoid duplicates
           &&(b-(y=M(a,c))?d==y:d-a&&d-b&&d-c) // and check if d must block a-c or it's free
           &&(
             e=M(b,d), // forced to block b-d
             f=M(c,e),g=M(a,e),g<f?[f,g]=[g,f]:0, // f and g could be in the wrong order
             r=a+b+c+d+e, // start building a return string
             x.push(r+f+g,r+g+f) // store all values in x
  )]&&x[n] // return value at requested position

Answer 2

Octave, 467 369 363 309 297 characters

297:

global t=0*(1:9)m=dec2bin([15;113;897;1170;1316;1608;2370;2216;2580])-48 a;
function g(s,p)global a t m;
if nnz(s)<8&&any((t==1)*m>2)a=[a;s];return;end;q=t==3-p;
(r=sort(~q.*(1:9)*m(:,find([3 1]*([q;t==p]*m)==6)')))||(r=find(~t));
for i=r t(i)=p;g([s i+47],3-p);t(i)=0;end;end;g('',1);f=@(n)a(n+1,:);

The only relevant change is that we never check if the current player can win, only check the opponent's possibility to win the next turn. As the only turn the player 1 can win is turn 7, this is the only place when the algorithm would produce game that is not optimal, but it's very easy to filter such a situation out. We simply verify each game generated if it's won by player 1 - if it was not, the move in turn 7 was incorrect, so we don't add this game to optimal games table.

(Exactly half the games generated by this rule are false ie. in the 7th turn the player 1 always has two possibilities to block player two, but only one will make him win instantly).

Use:

$ octave
octave:1>> source script.m
octave:2>> f(634)
ans = 3270148

The ungolfed code looks like:

 global t=0*(1:9);
 global m=dec2bin([15;113;897;1170;1316;1608;2370;2216;2580])-48;
 global allgames;
 allgames=[];

 function r=canbewon(by)
  global t m
  q=[t==by;t==(3-by)]*m;
  g=(find([3 1]*q==6))';
  r=sort((~(t==by).*(1:9)) * m(:,g));
 end

 function games_starting_with(s)
 global allgames t;
 if 7==numel(s) && any((t==1)*m==3) # it's 7th move and first player won
  allgames=[allgames;s];
  return;
 end;
 poss=(find(~t));                  # for now all free slots are possible
 player=1+mod(numel(s),2);
 moves = canbewon(3-player);
 if numel(moves) poss=moves; end;  # ... no, we must block the other player
 for i=poss
  t(i)=player;
  games_starting_with([s char(i+47)]);
  t(i)=0;
 end
end

games_starting_with('');
f=@(n)(allgames(n+1,:));