16
3
Background
An L-system (or Lindenmayer system) is a parallel rewriting system that, among other things, can be easily used to model fractals. This question concerns deterministic, context-free L-systems. These consists of an alphabet of symbols, an initial axiom string and a set of rewrite rules mapping each alphabet symbol to a new string. The rules are applied to the axiom in parallel, generating a new string. This process is then repeated.
For example, the system with the axiom "A" and the rules A=ABA;B=BBB generates the sequence of strings "ABA", "ABABBBABA", "ABABBBABABBBBBBBBBABABBBABA", etc. For conciseness, we don't explicitly mention the alphabet when defining the L-system. Furthermore, any symbol without an explicit rewrite rule is assumed to be unchanged (i.e. the default rule for a symbol A is A=A).
L-systems can be visualised using a form of turtle graphics. By convention, the turtle starts facing to the right. A string is then drawn by iterating over its symbols: an F means "draw forward one unit", a G means "move forward one unit", a + means "turn left one angle unit" and a - means "turn right one angle unit". All other symbols in the string are ignored. For the purpose of this question, the angle units are assumed to always be 90°.
Task
Given a specification of any L-system and a number of iterations, your program should output an ASCII rendering of the resulting string (as described above) using box-drawing characters.
- The parameters are passed in as a space-separated string comprising the axiom, rewrite rules (as a ;-separated list of equations) and number of rewrite iterations. For example, the input "F F=FGF;G=GGG 2" generates the string "FGFGGGFGF" and hence draws four lines with appropriate gaps.
- The symbols used by the L-system can be any ASCII character apart from space and semicolon. There is at most one explicit rule specified per symbol (with the default rewrite rule being the identity mapping as described above).
- You can assume that the output will always contain at least one F.
- The output should use the following UNICODE box-drawing characters to represent the visualization: ─ (U+2500), │ (U+2502), ┌ (U+250C), ┐ (U+2510), └ (U+2514), ┘ (U+2518), ├ (U+251C), ┤ (U+2524), ┬ (U+252C), ┴ (U+2534), ┼ (U+253C), ╴ (U+2574), ╵ (U+2575), ╶ (U+2576) and ╷ (U+2577). See below for examples.
- The output should not contain empty lines above the topmost box character or below the bottommost one. It should also not contain any spaces to the left of the leftmost box characer or to the right of the rightmost one. Lines with trailing spaces that don't extend beyond the rightmost box character are allowed.
You may write a program or function, taking input via STDIN (or closest alternative), command-line argument or function argument. Results should be printed to STDOUT (or closest alternative), saved to a file or returned as a string.
Examples
# Cantor dust
>> "F F=FGF;G=GGG 0"
╶╴
>> "F F=FGF;G=GGG 1"
╶╴╶╴
>> "F F=FGF;G=GGG 2"
╶╴╶╴ ╶╴╶╴
>> "F F=FGF;G=GGG 3"
╶╴╶╴ ╶╴╶╴ ╶╴╶╴ ╶╴╶╴
# Koch curve
>> "F F=F+F−F−F+F 1"
┌┐
╶┘└╴
>> "F F=F+F-F-F+F 2"
┌┐
┌┘└┐
┌┘ └┐
┌┼┐ ┌┼┐
╶┘└┘ └┘└╴
Other examples to test your program with include:
# Dragon curve
>> "FX X=X+YF+;Y=-FX-Y n"
# Hilbert curve
>> "A A=-BF+AFA+FB-;B=+AF-BFB-FA+ n"
# Sierpinski carpet
>> "F F=F+F-F-F-G+F+F+F-F;G=GGG n"
The first two of which look as follows (produced using @edc65's answer):
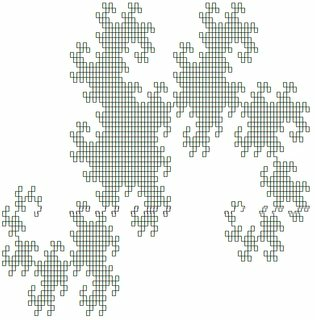

You can test out any of the systems at this page.
Scoring
Shortest code (in bytes) wins. Standard rules apply.
Miscellania
This challenge was inspired by Draw a Random Walk with Slashes. In fact, it's possible to represent a random walk as an L-system if we extend the system to allow multiple rules per symbol, with the expansion chosen non-determistically during rewriting. One formulation is:
"F F=FF;F=F+F;F=F++F;F=F+++F"
Another common extension, often used when modeling plants, is to interpret the [ and ] characters as pushing and popping the current position and angle. Most plants use angles smaller than 90°, but here is one example that doesn't:
"FAX X=[-FAX][FAX][+FAX];A=AFB;B=A"
Neither of these examples need to be supported in this challenge.
This challenge is also similar to "Sorry, young man, but it's Turtles all the way down!". However, that challenge used line rendering rather than ASCII and allowed a more flexible syntax.
Great (and quick!) answer. I've added screenshots of the dragon and hilbert curve outputs to the question. – Uri Granta – 2015-04-10T16:04:21.723