52
11
Since it was Pi day recently, I have noticed a number of challenges that ask you to calculate pi.
Of course, a quiche lorraine is not quite a pie (you can claim a Bonus Score¹ of +1 if you guessed the challenge off of the title). As such, your job is to write an algorithm or method that looks like it approximates Pi at first glance, but is guaranteed not to converge towards Pi.
This is an underhanded challenge, so make sure it will output 3.14... for a simple test case, e.g. with 10 iterations of your algorithm. This is also a popularity challenge, so don't go for the obvious echo(pi) and say that IEEE 754 floating point rounds some digits up or down.
Winner gets a quiche lorraine².
¹ Warning: not actually a bonus score. By claiming the score, you agree to bake me a pie before Pi Day, 2016
² Warning: quiche lorraine is used as a metaphor for having your answer marked as 'accepted'
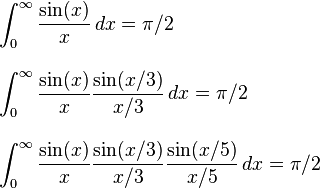
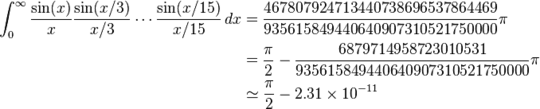
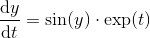
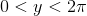
Related: link
– Sp3000 – 2015-03-19T13:06:31.7672
I'm voting to close this question as off-topic because underhanded challenges are no-longer on-topic here. http://meta.codegolf.stackexchange.com/a/8326/20469
– cat – 2016-04-15T14:20:18.403