Area of a Self-Intersecting Polygon

Question

Consider a potentially self-intersecting polygon, defined by a list of vertices in 2D space. E.g.

{{0, 0}, {5, 0}, {5, 4}, {1, 4}, {1, 2}, {3, 2}, {3, 3}, {2, 3}, {2, 1}, {4, 1}, {4, 5}, {0, 5}}

There are several ways to define the area of such a polygon, but the most interesting one is the even-odd rule. Taking any point in the plane, draw a line from the point out to infinity (in any direction). If that line crosses the polygon an odd number of times, the point is part of the polygon's area, if it crosses the polygon an even number of times, the point is not part of the polygon. For the above example polygon, here are both its outline as well as its even-odd area:

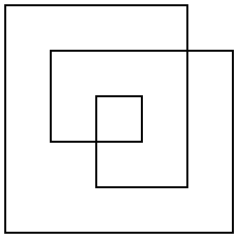
^{The polygon will not in general be orthogonal. I've only chosen such a simple example to make it easier to count the area.}

The area of this example is 17 (not 24 or 33 as other definitions or area might yield).

Note that under this definition the area of the polygon is independent of its winding order.

The Challenge

Given a list of vertices with integer coordinates defining a polygon, determine its area under the even-odd rule.

You may write a function or program, taking input via STDIN or closest alternative, command-line argument or function argument and either return the result or print it to STDOUT or closest alternative.

You may take input in any convenient list or string format, as long as it's not preprocessed.

The result should either be floating point number, accurate to 6 significant (decimal) digits, or a rational result whose floating point representation is accurate to 6 significant digits. (If you produce rational results they are likely going to be exact, but I can't require this, as I don't have exact results for reference.)

You must be able to solve each of the test cases below within 10 seconds on a reasonable desktop machine. (There is some leeway in this rule, so use your best judgement. If it takes 20 seconds on my laptop I'll give you the benefit of the doubt, if it takes a minute, I won't.) I think this limit should be very generous but it is supposed to rule out approaches where you just discretise the polygon on a sufficiently fine grid and count, or use probabilistic approaches like Monte Carlo. Be a good sportsman and don't try to optimise of these approaches such that you can meet the time limit anyway. ;)

You must not use any existing functions related directly to polygons.

This is code golf, so the shortest submission (in bytes) wins.

Assumptions

• All coordinates are integers in the range 0 ≤ x ≤ 100, 0 ≤ y ≤ 100.
• There will be at least 3 and at most 50 vertices.
• There won't be any repeated vertices. Neither will any vertices lie on another edge. (There may be collinear points in the list, though.)

Test Cases

{{0, 0}, {5, 0}, {5, 4}, {1, 4}, {1, 2}, {3, 2}, {3, 3}, {2, 3}, {2, 1}, {4, 1}, {4, 5}, {0, 5}}
17.0000

{{22, 87}, {6, 3}, {98, 77}, {20, 56}, {96, 52}, {79, 34}, {46, 78}, {52, 73}, {81, 85}, {90, 43}}
2788.39

{{90, 43}, {81, 85}, {52, 73}, {46, 78}, {79, 34}, {96, 52}, {20, 56}, {98, 77}, {6, 3}, {22, 87}}
2788.39

{{70, 33}, {53, 89}, {76, 35}, {14, 56}, {14, 47}, {59, 49}, {12, 32}, {22, 66}, {85, 2}, {2, 81},
 {61, 39}, {1, 49}, {91, 62}, {67, 7}, {19, 55}, {47, 44}, {8, 24}, {46, 18}, {63, 64}, {23, 30}}
2037.98

{{42, 65}, {14, 59}, {97, 10}, {13, 1}, {2, 8}, {88, 80}, {24, 36}, {95, 94}, {18, 9}, {66, 64},
 {91, 5}, {99, 25}, {6, 66}, {48, 55}, {83, 54}, {15, 65}, {10, 60}, {35, 86}, {44, 19}, {48, 43},
 {47, 86}, {29, 5}, {15, 45}, {75, 41}, {9, 9}, {23, 100}, {22, 82}, {34, 21}, {7, 34}, {54, 83}}
3382.46

{{68, 35}, {43, 63}, {66, 98}, {60, 56}, {57, 44}, {90, 52}, {36, 26}, {23, 55}, {66, 1}, {25, 6},
 {84, 65}, {38, 16}, {47, 31}, {44, 90}, {2, 30}, {87, 40}, {19, 51}, {75, 5}, {31, 94}, {85, 56},
 {95, 81}, {79, 80}, {82, 45}, {95, 10}, {27, 15}, {18, 70}, {24, 6}, {12, 73}, {10, 31}, {4, 29},
 {79, 93}, {45, 85}, {12, 10}, {89, 70}, {46, 5}, {56, 67}, {58, 59}, {92, 19}, {83, 49}, {22,77}}
3337.62

{{15, 22}, {71, 65}, {12, 35}, {30, 92}, {12, 92}, {97, 31}, {4, 32}, {39, 43}, {11, 40}, 
 {20, 15}, {71, 100}, {84, 76}, {51, 98}, {35, 94}, {46, 54}, {89, 49}, {28, 35}, {65, 42}, 
 {31, 41}, {48, 34}, {57, 46}, {14, 20}, {45, 28}, {82, 65}, {88, 78}, {55, 30}, {30, 27}, 
 {26, 47}, {51, 93}, {9, 95}, {56, 82}, {86, 56}, {46, 28}, {62, 70}, {98, 10}, {3, 39}, 
 {11, 34}, {17, 64}, {36, 42}, {52, 100}, {38, 11}, {83, 14}, {5, 17}, {72, 70}, {3, 97}, 
 {8, 94}, {64, 60}, {47, 25}, {99, 26}, {99, 69}}
3514.46

Answer 1

Mathematica, 247 225 222

p=Partition[#,2,1,1]&;{a_,b_}~r~{c_,d_}=Det/@{{a-c,c-d},{a,c}-b}/Det@{a-b,c-d};f=Abs@Tr@MapIndexed[Det@#(-1)^Tr@#2&,p[Join@@MapThread[{1-#,#}&/@#.#2&,{Sort/@Cases[{s_,t_}/;0<=s<=1&&0<=t<=1:>s]/@Outer[r,#,#,1],#}]&@p@#]]/2&

First add the points of intersection to the polygon, then reverse some of the edges, then its area can be calculated just like a simple polygon.

Example:

In[2]:= f[{{15, 22}, {71, 65}, {12, 35}, {30, 92}, {12, 92}, {97, 31}, {4, 32}, {39, 43}, {11, 40}, 
 {20, 15}, {71, 100}, {84, 76}, {51, 98}, {35, 94}, {46, 54}, {89, 49}, {28, 35}, {65, 42}, 
 {31, 41}, {48, 34}, {57, 46}, {14, 20}, {45, 28}, {82, 65}, {88, 78}, {55, 30}, {30, 27}, 
 {26, 47}, {51, 93}, {9, 95}, {56, 82}, {86, 56}, {46, 28}, {62, 70}, {98, 10}, {3, 39}, 
 {11, 34}, {17, 64}, {36, 42}, {52, 100}, {38, 11}, {83, 14}, {5, 17}, {72, 70}, {3, 97}, 
 {8, 94}, {64, 60}, {47, 25}, {99, 26}, {99, 69}}]

Out[2]= 3387239559852305316061173112486233884246606945138074528363622677708164\
 6419838924305735780894917246019722157041758816629529815853144003636562\
 9161985438389053702901286180223793349646170997160308182712593965484705\
 3835036745220226127640955614326918918917441670126958689133216326862597\
 0109115619/\
 9638019709367685232385259132839493819254557312303005906194701440047547\
 1858644412915045826470099500628074171987058850811809594585138874868123\
 9385516082170539979030155851141050766098510400285425157652696115518756\
 3100504682294718279622934291498595327654955812053471272558217892957057\
 556160

In[3]:= N[%] (*The numerical value of the last output*)

Out[3]= 3514.46

Answer 2

Python 2, 323 319 bytes

exec u"def I(s,a,b=1j):c,d=s;d-=c;c-=a;e=(d*bX;return e*(0<=(b*cX*e<=e*e)and[a+(d*cX*b/e]or[]\nE=lambda p:zip(p,p[1:]+p);S=sorted;P=E(input());print sum((t-b)*(r-l)/2Fl,r@E(S(i.realFa,b@PFe@PFi@I(e,a,b-a)))[:-1]Fb,t@E(S(((i+j)XFe@PFi@I(e,l)Fj@I(e,r)))[::2])".translate({70:u" for ",64:u" in ",88:u".conjugate()).imag"})

Takes a list of vertices through STDIN as complex numbers, in the following form

[  X + Yj,  X + Yj,  ...  ]

, and writes the result to STDOUT.

Same code after string replacement and some spacing:

def I(s, a, b = 1j):
    c, d = s; d -= c; c -= a;
    e = (d*b.conjugate()).imag;
    return e * (0 <= (b*c.conjugate()).imag * e <= e*e) and \
           [a + (d*c.conjugate()).imag * b/e] or []

E = lambda p: zip(p, p[1:] + p);
S = sorted;

P = E(input());

print sum(
    (t - b) * (r - l) / 2

    for l, r in E(S(
        i.real for a, b in P for e in P for i in I(e, a, b - a)
    ))[:-1]

    for b, t in E(S(
        ((i + j).conjugate()).imag for e in P for i in I(e, l) for j in I(e, r)
    ))[::2]
)

Explanation

For each point of intersection of two sides of the input polygon (including the vertices), pass a vertical line though that point.

(In fact, due to golfing, the program passes a few more lines; it doesn't really matter, as long as we pass at least these lines.) The body of the polygon between any two consecutive lines is comprised of vertical trapezoids (and triangles, and line segments, as special cases of those). It has to be the case, since if any of these shapes had an additional vertex between the two bases, there would be another vertical line through that point, between the two lines in question. The sum of the areas of all such trapezoids is the area of the polygon.

Here's how we find these trapezoids: For each pair of consecutive vertical lines, we find the segments of each side of the polygon that (properly) lie between these two lines (which might not exist for some of the sides). In the above illustration, these are the six red segments, when considering the two red vertical lines. Note that these segments don't properly intersect each other (i.e., they may only meet at their end points, completely coincide or not intersect at all, since, once again, if they properly intersected there would be another vertical line in between;) and so it makes sense to talk about ordering them top-to-bottom, which we do. According to the even-odd rule, once we cross the first segment, we're inside the polygon; once we cross the second one, we're out; the third one, in again; the fourth, out; and so on... In other words, if we group the segments into consecutive pairs, each pair is the legs of one of the trapezoids.

Overall, this is an O(n³ log n) algorithm.

Answer 3

Haskell, 549

It doesn't look like I can golf this one down far enough, but the concept was different than the other two answers so I figured I'd share it anyway. It performs O(N^2) rational operations to compute the area.

import Data.List
_%0=2;x%y=x/y
h=sort
z f w@(x:y)=zipWith f(y++[x])w
a=(%2).sum.z(#);(a,b)#(c,d)=b*c-a*d
(r,p)?(s,q)=[(0,p)|p==q]++[(t,v t p r)|u t,u$f r]where f x=(d q p#x)%(r#s);t=f s;u x=x^2<x
v t(x,y)(a,b)=(x+t*a,y+t*b);d=v(-1)
s x=zip(z d x)x
i y=h.(=<<y).(?)=<<y
[]!x=[x];x!_=x
e n(a@(x,p):y)|x>0=(n!y,a):(e(n!y)$tail$dropWhile((/=p).snd)y)|0<1=(n,a):e n y
c[p]k=w x[]where((_,q):x)=e[]p;w((n,y):z)b|q==y=(k,map snd(q:b)):c n(-k)|0<1=w z(y:b);c[]_=[]
b(s,p)=s*a p
u(_,x)(_,y)=h x==h y
f p=abs$sum$map b$nubBy u$take(length p^2)$c[cycle$i$s p]1

Example:

λ> f test''
33872395598523053160611731124862338842466069451380745283636226777081646419838924305735780894917246019722157041758816629529815853144003636562916198543838905370290128618022379334964617099716030818271259396548470538350367452202261276409556143269189189174416701269586891332163268625970109115619 % 9638019709367685232385259132839493819254557312303005906194701440047547185864441291504582647009950062807417198705885081180959458513887486812393855160821705399790301558511410507660985104002854251576526961155187563100504682294718279622934291498595327654955812053471272558217892957057556160
λ> fromRational (f test'')
3514.4559380388832

The idea is to rewire the polygon at every crossing, resulting in a union of polygons with no intersecting edges. We can then compute the (signed) area of each of the polygons using Gauss' shoelace formula (http://en.wikipedia.org/wiki/Shoelace_formula). The even-odd rule demands that when a crossing is converted, the area of the new polygon is counted negatively relative to the old polygon.

For example, consider the polygon in the original question. The crossing in the upper-left is converted to two paths which only meet at a point; the two paths are both oriented clockwise, so the areas of each would be positive unless we declared that the inner path is weighted by -1 relative to the outer path. This is equivalent to alphaalpha's path reversal.

As another example, consider the polygon from MickyT's comment:

Here, some of the polygons are oriented clockwise and some counterclockwise. The sign-flip-on-crossing rule ensures that the clockwise-oriented regions pick up an extra factor of -1, causing them to contribute a positive amount to the area.

Here's how the program works:

import Data.List  -- for sort and nubBy

-- Rational division, with the unusual convention that x/0 = 2
_%0=2;x%y=x/y

-- Golf
h=sort

-- Define a "cyclic zipWith" operation. Given a list [a,b,c,...z] and a binary
-- operation (@), z (@) [a,b,c,..z] computes the list [b@a, c@b, ..., z@y, a@z]
z f w@(x:y)=zipWith f(y++[x])w

-- The shoelace formula for the signed area of a polygon
a=(%2).sum.z(#)

-- The "cross-product" of two 2d vectors, resulting in a scalar.
(a,b)#(c,d)=b*c-a*d

-- Determine if the line segment from p to p+r intersects the segment from
-- q to q+s.  Evaluates to the singleton list [(t,x)] where p + tr = x is the
-- point of intersection, or the empty list if there is no intersection. 
(r,p)?(s,q)=[(0,p)|p==q]++[(t,v t p r)|u t,u$f r]where f x=(d q p#x)%(r#s);t=f s;u x=x^2<x

-- v computes an affine combination of two vectors; d computes the difference
-- of two vectors.
v t(x,y)(a,b)=(x+t*a,y+t*b);d=v(-1)

-- If x is a list of points describing a polygon, s x will be the list of
-- (displacement, point) pairs describing the edges.
s x=zip(z d x)x

-- Given a list of (displacement, point) pairs describing a polygon's edges,
-- create a new polygon which also has a vertex at every point of intersection.
-- Mercilessly golfed.
i y=h.(=<<y).(?)=<<y


-- Extract a simple polygon; when an intersection point is reached, fast-forward
-- through the polygon until we return to the same point, then continue.  This
-- implements the edge rewiring operation. Also keep track of the first
-- intersection point we saw, so that we can process that polygon next and with
-- opposite sign.
[]!x=[x];x!_=x
e n(a@(x,p):y)|x>0=(n!y,a):(e(n!y)$tail$dropWhile((/=p).snd)y)|0<1=(n,a):e n y

-- Traverse the polygon from some arbitrary starting point, using e to extract
-- simple polygons marked with +/-1 weights.
c[p]k=w x[]where((_,q):x)=e[]p;w((n,y):z)b|q==y=(k,map snd(q:b)):c n(-k)|0<1=w z(y:b);c[]_=[]

-- If the original polygon had N vertices, there could (very conservatively)
-- be up to N^2 points of intersection.  So extract N^2 polygons using c,
-- throwing away duplicates, and add up the weighted areas of each polygon.
b(s,p)=s*a p
u(_,x)(_,y)=h x==h y
f p=abs$sum$map b$nubBy u$take(length p^2)$c[cycle$i$s p]1