Create a universal two-dimensional cellular automaton cell using two-way universal logic processors

Question

In Conway's Game of Life, a cell is in a state of either on or off, depending on the on-and-off state of the eight cells surrounding it.

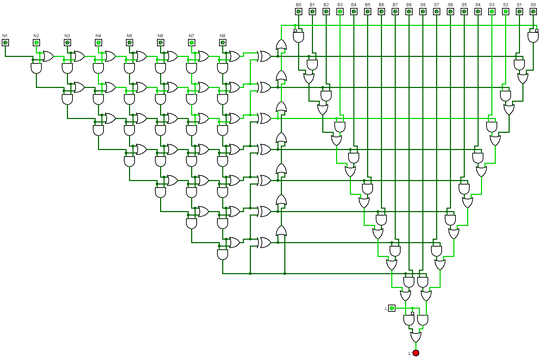
We can simulate this using a logic gate network with some sort of clock signal that updates every cell all at once. Your task in this problem is to build the logic gate network for a single cell that will update the new state of the cell given the state of its neighbours.

This cell is a logic gate network that takes eight neighbour-cell inputs N1, N2, ..., N8, the current on/off state of its own cell L, and 18 "rule" inputs B0, B1, B2, ..., B8 and S0, S1, S2, ..., S8, and evaluates a new L value (to an output L') as follows:

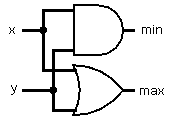
• if L is currently 0 and Bn is on where n is the number of N1, N2, ..., N8 that are currently set at 1, then L' is set to 1. Otherwise, it stays 0.

• if L is currently 1 and Sn is off where n is the number of N1, N2, ..., N8 that are currently set at 1, then L' is set to 0. Otherwise, it stays 1.

In the example of Conway's Game of Life, B3, S3, and S2 are on, while the rest of them are all off.

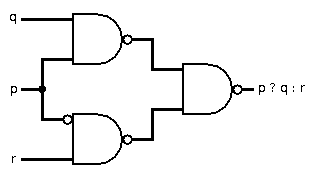
Unlike my previous logic gate tasks, for this task you may use any two-input logic gates you want, not just NAND gates. This includes exotic gates such as if A then B, A or not B, or simply A, a gate that takes two inputs and always returns the first one (although I'm not sure why you'd want to use that one, you are allowed to). You are allowed unlimited constants, splits, and ground wires.

The network to use the fewest logic gates to achieve this wins.

Answer 1

89 gates using sorting network

I think the basic structure pretty much has to be a sum unit and a demultiplexer which uses the output of the sum unit and L to select the appropriate B_i or S_i. So there's one decision which is definitely interesting, and one dependent decision which may be interesting.

The definitely interesting decision is the output format of the sum. The dependent decision is whether to structure the 18-value demux as two 9-value demuxes (switched by the sum) feeding into a 2-value demux (switched by L) or as 9 2-value demuxes feeding into a 9-value demux.

I'm choosing to have the sum output in unary, so the 9-value demux is just 8 2-input demuxes in a chain, and the dependent decision is uninteresting.

Counting in unary via sorting network

AND and OR gates can be considered instead to be MIN and MAX gates, giving a two-gate way of sorting two bits:

These pairwise sorting operators can be combined to sort any number of bits (and, if generalised to MIN and MAX operations over any total order, to sort any number of elements of that order) in a sorting network. The standard notation shows just which lines are sorted at each step, and drawing the gates would be quite messy. The best possible sorting network for 8 inputs requires 19 pairwise sorters, which can be arranged as so:

So for a total of 38 gates, the inputs N1 to N8 are transformed into 8 intermediate values T1 = MAX(N1, ..., N8) to T8 = MIN(N1, ..., N8). Effectively Ti is true iff at least i of the inputs are true.

Demultiplexing

A 2-value demultiplexer can be done with 3 gates in many many ways. E.g.

An n-value demux taking unary input S_i and selecting between values V_i can be built up recursively from n-1 2-value demuxes as follows:

d_0 = V_0
d_{i+1} = S_{i+1} ? V_{i+1} : d_i

So two 9-value demuxes and a 2-value demux takes 17 demuxes; so does 9 2-value demuxes and a single 9-value demux.

So the grand total gate count is 38 for the sorting network + 17*3 for the demuxes, giving 89.

Answer 2

114 107 gates

A diagram of the setup, with example inputs (link to full-sized image):

Created in Logisim

This uses a simple approach; first it counts the number of live neighbouring cells, and then checks if that number fulfills a birth/survival condition.