Python 2 with PIL
This is still somewhat a work in progress. Also, the code below is a horrible mess of spaghetti, and should not be used as an inspiration. :)
from PIL import Image, ImageFilter
from math import sqrt
from copy import copy
from random import shuffle, choice, seed
IN_FILE = "input.png"
OUT_FILE = "output.png"
LOGGING = True
GRAPHICAL_LOGGING = False
LOG_FILE_PREFIX = "out"
LOG_FILE_SUFFIX = ".png"
LOG_ROUND_INTERVAL = 150
LOG_FLIP_INTERVAL = 40000
N = 500
P = 30
BLUR_RADIUS = 3
FILAMENT_ROUND_INTERVAL = 5
seed(0) # Random seed
print("Opening input file...")
image = Image.open(IN_FILE).filter(ImageFilter.GaussianBlur(BLUR_RADIUS))
pixels = {}
width, height = image.size
for i in range(width):
for j in range(height):
pixels[(i, j)] = image.getpixel((i, j))
def dist_rgb((a,b,c), (d,e,f)):
return (a-d)**2 + (b-e)**2 + (c-f)**2
def nbors((x,y)):
if 0 < x:
if 0 < y:
yield (x-1,y-1)
if y < height-1:
yield (x-1,y+1)
if x < width - 1:
if 0 < y:
yield (x+1,y-1)
if y < height-1:
yield (x+1,y+1)
def full_circ((x,y)):
return ((x+1,y), (x+1,y+1), (x,y+1), (x-1,y+1), (x-1,y), (x-1,y-1), (x,y-1), (x+1,y-1))
class Region:
def __init__(self):
self.points = set()
self.size = 0
self.sum = (0,0,0)
def flip_point(self, point):
sum_r, sum_g, sum_b = self.sum
r, g, b = pixels[point]
if point in self.points:
self.sum = (sum_r - r, sum_g - g, sum_b - b)
self.size -= 1
self.points.remove(point)
else:
self.sum = (sum_r + r, sum_g + g, sum_b + b)
self.size += 1
self.points.add(point)
def mean_with(self, color):
if color is None:
s = float(self.size)
r, g, b = self.sum
else:
s = float(self.size + 1)
r, g, b = map(lambda a,b: a+b, self.sum, color)
return (r/s, g/s, b/s)
print("Initializing regions...")
aspect_ratio = width / float(height)
a = int(sqrt(N)*aspect_ratio)
b = int(sqrt(N)/aspect_ratio)
num_components = a*b
owners = {}
regions = [Region() for i in range(P)]
borders = set()
nodes = [(i,j) for i in range(a) for j in range(b)]
shuffle(nodes)
node_values = {(i,j):None for i in range(a) for j in range(b)}
for i in range(P):
node_values[nodes[i]] = regions[i]
for (i,j) in nodes[P:]:
forbiddens = set()
for node in (i,j-1), (i,j+1), (i-1,j), (i+1,j):
if node in node_values and node_values[node] is not None:
forbiddens.add(node_values[node])
node_values[(i,j)] = choice(list(set(regions) - forbiddens))
for (i,j) in nodes:
for x in range((width*i)/a, (width*(i+1))/a):
for y in range((height*j)/b, (height*(j+1))/b):
owner = node_values[(i,j)]
owner.flip_point((x,y))
owners[(x,y)] = owner
def recalc_borders(point = None):
global borders
if point is None:
borders = set()
for i in range(width):
for j in range(height):
if (i,j) not in borders:
owner = owner_of((i,j))
for pt in nbors((i,j)):
if owner_of(pt) != owner:
borders.add((i,j))
borders.add(pt)
break
else:
for pt in nbors(point):
owner = owner_of(pt)
for pt2 in nbors(pt):
if owner_of(pt2) != owner:
borders.add(pt)
break
else:
borders.discard(pt)
def owner_of(point):
if 0 <= point[0] < width and 0 <= point[1] < height:
return owners[point]
else:
return None
# Status codes for analysis
SINGLETON = 0
FILAMENT = 1
SWAPPABLE = 2
NOT_SWAPPABLE = 3
def analyze_nbors(point):
owner = owner_of(point)
circ = a,b,c,d,e,f,g,h = full_circ(point)
oa,ob,oc,od,oe,of,og,oh = map(owner_of, circ)
nbor_owners = set([oa,oc,oe,og])
if owner not in nbor_owners:
return SINGLETON, owner, nbor_owners - set([None])
if oc != oe == owner == oa != og != oc:
return FILAMENT, owner, set([og, oc]) - set([None])
if oe != oc == owner == og != oa != oe:
return FILAMENT, owner, set([oe, oa]) - set([None])
last_owner = oa
flips = {last_owner:0}
for (corner, side, corner_owner, side_owner) in (b,c,ob,oc), (d,e,od,oe), (f,g,of,og), (h,a,oh,oa):
if side_owner not in flips:
flips[side_owner] = 0
if side_owner != corner_owner or side_owner != last_owner:
flips[side_owner] += 1
flips[last_owner] += 1
last_owner = side_owner
candidates = set(own for own in flips if flips[own] == 2 and own is not None)
if owner in candidates:
return SWAPPABLE, owner, candidates - set([owner])
return NOT_SWAPPABLE, None, None
print("Calculating borders...")
recalc_borders()
print("Deforming regions...")
def assign_colors():
used_colors = {}
for region in regions:
r, g, b = region.mean_with(None)
r, g, b = int(round(r)), int(round(g)), int(round(b))
if (r,g,b) in used_colors:
for color in sorted([(r2, g2, b2) for r2 in range(256) for g2 in range(256) for b2 in range(256)], key=lambda color: dist_rgb(color, (r,g,b))):
if color not in used_colors:
used_colors[color] = region.points
break
else:
used_colors[(r,g,b)] = region.points
return used_colors
def make_image(colors):
img = Image.new("RGB", image.size)
for color in colors:
for point in colors[color]:
img.putpixel(point, color)
return img
# Round status labels
FULL_ROUND = 0
NEIGHBOR_ROUND = 1
FILAMENT_ROUND = 2
max_filament = None
next_search = set()
rounds = 0
points_flipped = 0
singletons = 0
filaments = 0
flip_milestone = 0
logs = 0
while True:
if LOGGING and (rounds % LOG_ROUND_INTERVAL == 0 or points_flipped >= flip_milestone):
print("Round %d of deformation:\n %d edit(s) so far, of which %d singleton removal(s) and %d filament cut(s)."%(rounds, points_flipped, singletons, filaments))
while points_flipped >= flip_milestone: flip_milestone += LOG_FLIP_INTERVAL
if GRAPHICAL_LOGGING:
make_image(assign_colors()).save(LOG_FILE_PREFIX + str(logs) + LOG_FILE_SUFFIX)
logs += 1
if max_filament is None or (round_status == NEIGHBOR_ROUND and rounds%FILAMENT_ROUND_INTERVAL != 0):
search_space, round_status = (next_search & borders, NEIGHBOR_ROUND) if next_search else (copy(borders), FULL_ROUND)
next_search = set()
max_filament = None
else:
round_status = FILAMENT_ROUND
search_space = set([max_filament[0]]) & borders
search_space = list(search_space)
shuffle(search_space)
for point in search_space:
status, owner, takers = analyze_nbors(point)
if (status == FILAMENT and num_components < N) or status in (SINGLETON, SWAPPABLE):
color = pixels[point]
takers_list = list(takers)
shuffle(takers_list)
for taker in takers_list:
dist = dist_rgb(color, owner.mean_with(None)) - dist_rgb(color, taker.mean_with(color))
if dist > 0:
if status != FILAMENT or round_status == FILAMENT_ROUND:
found = True
owner.flip_point(point)
taker.flip_point(point)
owners[point] = taker
recalc_borders(point)
next_search.add(point)
for nbor in full_circ(point):
next_search.add(nbor)
points_flipped += 1
if status == FILAMENT:
if round_status == FILAMENT_ROUND:
num_components += 1
filaments += 1
elif max_filament is None or max_filament[1] < dist:
max_filament = (point, dist)
if status == SINGLETON:
num_components -= 1
singletons += 1
break
rounds += 1
if round_status == FILAMENT_ROUND:
max_filament = None
if round_status == FULL_ROUND and max_filament is None and not next_search:
break
print("Deformation completed after %d rounds:\n %d edit(s), of which %d singleton removal(s) and %d filament cut(s)."%(rounds, points_flipped, singletons, filaments))
print("Assigning colors...")
used_colors = assign_colors()
print("Producing output...")
make_image(used_colors).save(OUT_FILE)
print("Done!")
How it works
The program divides the canvas into P regions, each of which consists of some number of cells without holes. Initially, the canvas is just divided into approximate squares, which are randomly assigned to the regions. Then, these regions are "deformed" in an iterative process, where a given pixel can change its region if
- the change would decrease the pixel's RGB distance from the average color of the region that contains it, and
- it does not break or merge cells or introduce holes in them.
The latter condition can be enforced locally, so the process is a bit like a cellular automaton. This way, we don't have to do any pathfinding or such, which speeds the process up greatly. However, since the cells can't be broken up, some of them end up as long "filaments" that border other cells and inhibit their growth. To fix this, there is a process called "filament cut", which occasionally breaks a filament-shaped cell in two, if there are less than N cells at that time. Cells can also disappear if their size is 1, and this makes room for the filaments cuts.
The process ends when no pixel has the incentive to switch regions, and after that, each region is simply colored by its average color. Usually there will be some filaments remaining in the output, as can be seen in the examples below, especially in the nebula.
P = 30, N = 500


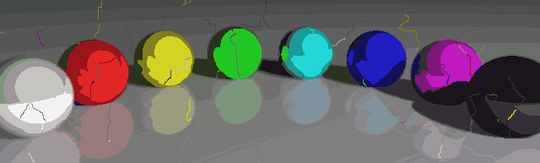

More pictures later.
Some interesting properties of my program are that it is probabilistic, so that the results may vary between different runs, unless you use the same pseudorandom seed of course. The randomness is not essential, though, I just wanted to avoid any accidental artifacts that may result from the particular way Python traverses a set of coordinates or something similar. The program tends to use all P colors and almost all N cells, and the cells never contain holes by design. Also, the deformation process is quite slow. The colored balls took almost 15 minutes to produce on my machine. On the upside, it you turn on the GRAPHICAL_LOGGING option, you'll get a cool series of pictures of the deformation process. I made the Mona Lisa ones into a GIF animation (shrunk 50 % to reduce the file size). If you look closely at her face and hair, you can see the filament cutting process in action.
































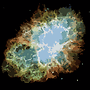










































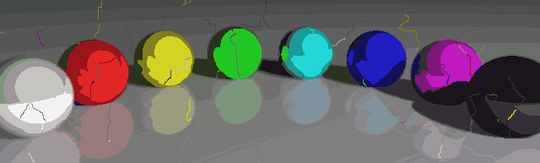


This is a fascinating post. Has anyone gone the extra step of adding the color numbers like an actual Paint by Number? – B. Blair – 2017-11-17T19:10:26.027
2
Not the most efficient thing, but here's a Python 2 PIL verifier.
– Sp3000 – 2014-12-08T09:29:13.947What a lovely question but I was hoping we would also see the proper "paint by numbers " version. That is with numbers in place so I could use the answers :) – None – 2014-12-10T11:03:17.497
@Lembik I originally wanted to include that, but I felt that it distracted from the interesting part of the question. It shouldn't be too hard to take the output of one of the submissions and convert into a template, though. – Martin Ender – 2014-12-10T11:06:03.313