Evaluate CDF of Student-t distribution

Question

The goal of this codegolf is evaluating the cumulative distribution function of the student-t probability distribution. This is not trivial since there is no closed form and the function is dependent of two variables v and x. The distribution function is

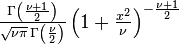
For getting the CDF you could integrate this function from -inf to x. As you can see the evaluation of this function relies much on integration as you'd also have to evaluate nontrivial values of the gamma function.

Details

You can can write a program or function that accepts a two numbers xand v as input, where x is the position (must at least accept floats from -10 upto 10) at which the CDF is evaluated and v is the number of degrees of freedom. v is a positive integer (range 1 upto 1450) but it must be possible to set it to infinity (for v=inf the student-t distribution is equal to the normal distribution). But you can specify that e.g. v = -1 should denote infinity. The output consists must be a number between 0 and 1 and must have an accuracy of at least 4 decimal places. If your language does not support runtime inputs or arguments on program call you may assume that both arguments are stored in variables (or another 'memory unit')

Restrictions

You may not use special functions like the gamma function or probability distribution functions as well as numerical integration functions or libraries (as long as you do not include their source in your code which counts for the score) etc. The idea is using only basic math functions. I tried to make a list of what I consider as 'basic' but there might be others I forgot - if so please comment.

Explicitly allowed are

+ - / * 
% (modulo)
! (factorial for integers only)
&& || xor != e.t.c. (logical operators)
<< >> ^ e.t.c. (bitshift and bitwise operators)
** pow (powerfunction for floats like a^b including sqrt or and other roots)
sin cos tan arcsin arccos arctan arctan2
ln lb log(a,b)
rand() (generating pseudorandom numbers of UNIFORM distribution)

Scoring

Lowest number of bytes wins.

Entry

Please explain how your code works. Please show the output of your program for at least 5 different arguments. Among those should be the following three. For your own values please also provide 'exact' values (like from wolframalpha or what ever you prefer).

x = 0      v= (any)  (should return 0.5000)
x = 3.078  v= 1      (should return 0.9000
x = 2.5    v= 23     (should return 0.9900)

If possible, it would be great if you could provide some fancy plots of the values calculated with your program (the code for plotting does not count for the score).

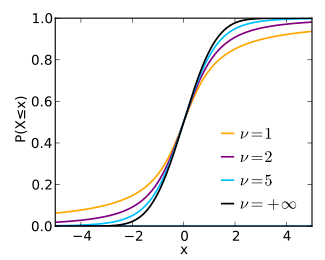
(from Wikipedia):

Answer 1

BBC BASIC, 155 ASCII characters, tokenised filesize 140

Download emulator at http://www.bbcbasic.co.uk/bbcwin/bbcwin.html

  a=1s=.000003INPUTx,v
  IFv<1v=9999
  FORw=1TOv-1a=w/a
  NEXTb=SGN(x)*s*a/SQR(v)IFv MOD2b=b/PI ELSEb=b/2
  f=.5FORz=0TOABS(x)STEPs
  f+=b/(1+z*z/v)^(v/2+.5)NEXTPRINTf

The code is in two parts. The first calculates the coefficient that is independent of x. and stores it in b. The algorithm is a bit like a continued fraction, but a mathematician would probably call it a simple quotient of two products. It's based on a formula from the Wikipedia page in the question, which is similar to a factorial but has the product (v-1)(v-3)... divided by the product (v-2)(v-4)... This is possible because we are only interested in half-integral values of the gamma function (arbitrary values of the gamma function would be a lot harder.) Using this formula we never have to calculate either gamma function, so we avoid large numbers. The largest intermediate value is approximately the square root of v.

The second is a straightforward integration from 0 to x by summation. It is known that f(0) is 0.5 so we start from there and work outwards. the sign and magnitude of b are modified before the loop, in order to be able to give the final answer directly.

Pretty version, ungolfed

This contains a few extra lines to add colour and to plot the data. The range x=0 to endpoint, and f(x)=0.5 to 1 is shown. Also v is modified to 2^v to be able to show the full range of v values without exceeding the limits on colour. In order to speed the drawing up, there are two less digits in s than in the golfed version. Even so, there is only one discrepancy when compared with http://www.wolframalpha.com/input/?i=student+t-distribution+probability: 0.8130575 rounds up to 0.8131. The golfed version give the correct answer (0.8130) for this and all the other cases below.

  a=1                              :REM accumulator for gamma series
  s=.0001                          :REM step size for x integration
  INPUTx,v
  IFv<1 v=9999                     :REM if v<1, set v to a value that gives results indistinguishable from infinity
  GCOLv                            :REM pick a colour
  v=2^v                            :REM for the pretty version, modify v to 2^v
  FORw=1TOv-1
    a=w/a                          :REM calculate series as per Wikipedia
  NEXT
  b=a/SQR(v)                       :REM divide a by the necessary values...
  IFv MOD2 b=b/PI ELSE b=b/2       :REM to give the coefficient, per Wikipedia

  b*=SGN(x)*s                      :REM modify according to sign and step size
  f=.5                             :REM initialise f(x)=.5 at x=0
  FORz=0TO ABS(x) STEPs
    f+=b/(1+z*z/v)^(v/2+.5)        :REM perform integration as simple "barchart" sum
    PLOT69,z*100+200,(f-.5)*1600   :REM plot a point
  NEXT
  PRINT f