13
4
Generate a Koch Snowflake
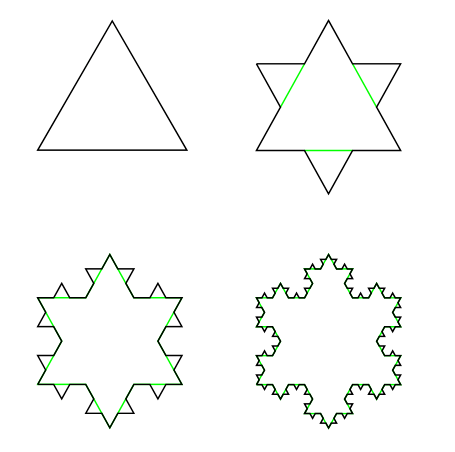
A Koch snowflake is a triangle that for each n, another equilateral point is added in the middle of each side: http://en.wikipedia.org/wiki/Koch_snowflake#Properties
We already had a kolmogrov-complexity Koch Snowflake challenge for n=4. The new challenge is to draw a Koch snowflake with any n between 1 and 10.
Rules
The snowflakes may not be hardcoded in the program or in files - they must be generated by your program.
Your program must support all sized
nbetween 1 and 10.The number of sides must be input by the user through std-in.
You must print a graphical representation of the snowflake to the screen.
Sample Koch Snowflakes with n equaling 1, 2, 3, and 4 (green lines for clarity only, do not reproduce them):
In the event of a tie-breaker, the program with the highest number of upvotes wins (pop-contest).

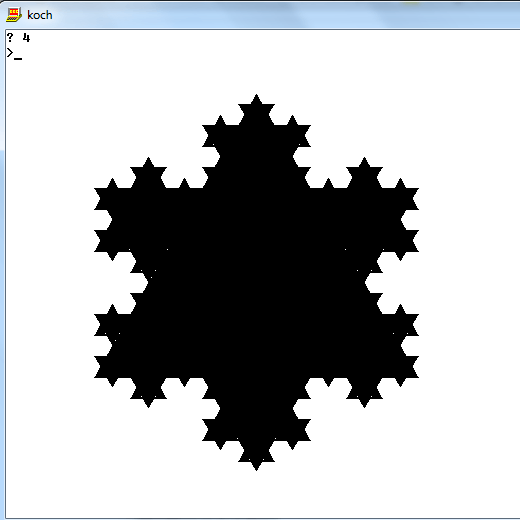
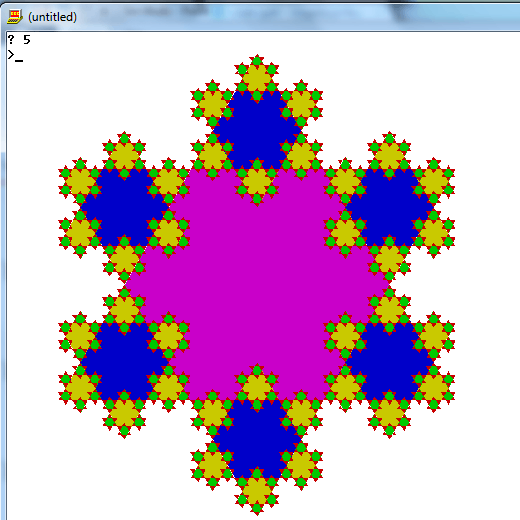



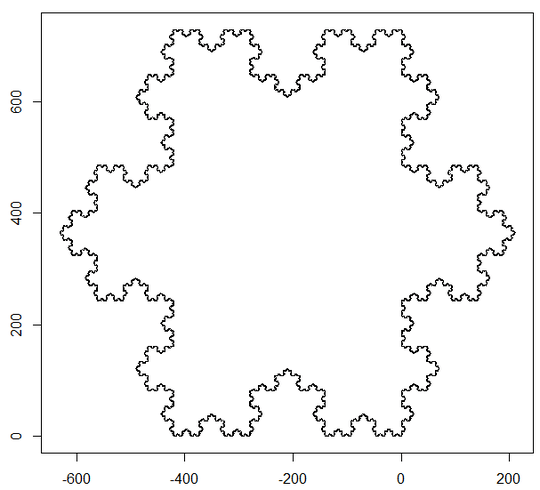
I'm not making sense of this: "You must use a function to calculate where to place the pixel. If your program does not have a built-in function for this purpose, you may deduct the cost of implementing one from your score." What pixel? – xnor – 2014-11-05T05:16:22.217
@xnor It was originally meant to calculate how to draw the snowflake on a per-pixel/character basis (the challenge was originally an ASCII-art challenge too). Most people will probably just use lines, so I will remove that. – None – 2014-11-05T05:17:57.657
Can one draw the whole snowflake filled in? – xnor – 2014-11-05T05:18:42.873
Of course. This comment needs to be longer. – None – 2014-11-05T05:19:48.283
Beyond
n=7, you can't see the newly added triangles in the snowflake on a computer screen. Is any "best effort" here OK? Is there a minimum resolution for pixel-based solutions? – xnor – 2014-11-05T05:23:14.993As long as they would be there if it was displayed large enough, you are alright. – None – 2014-11-05T05:25:05.097