Python, 1,291 1,271 1,225 bytes
As Martin noted, this problem can be largely reduced to his excellent rubber band challenge.
Using that challenge's terminology, we can take as the second set of nails the points of intersection between the circles on the boundary of the enclosed area:
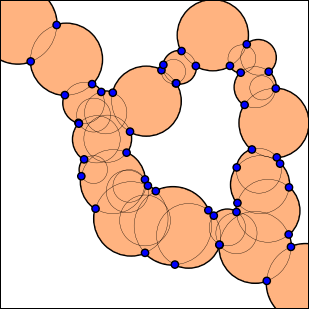
As the rubber band we can take any path P between the two endpoints that runs inside the enclosed area.
We can then invoke a solution to the rubber-band problem to produce a (locally) minimal path.
The challenge is, of course, to find such a path P, or more precisely, to find enough paths so that at least one of them produces the globally minimal path (note that in the first test-case we need at least one path to cover all possibilities, and in the second test-case at least two.)
A naive approach would be to just try all possible paths:
For every sequence of adjacent (i.e. intersecting) circles that connects the two endpoints, take the path along their centers (when two circles intersect, the segment between their centers is always within their union.)
Though this approach is technically correct, it can lead to a ridiculously large number of paths.
While I was able to solve the first test-case using this approach within a few seconds, the second one took forever.
Still, we can take this method as a starting point and try to minimize the number of paths we have to test.
This is what follows.
We construct our paths by basically performing a depth-first search on the graph of circles.
We're looking for a way to eliminate potential search directions at each step of the search.
Suppose that at some point we're at a circle A, that has two adjacent circles B and C, which are also adjacent to each other.
We can get from A to C by visiting B (and vice versa,) so we might think that visiting both B and C directly from A is unnecessary.
Unfortunately, this is wrong, as this illustration shows:
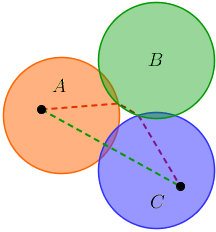
If the points in the illustration are the two endpoints, we can see that by going from A to C through B we get a longer path.
How about this one: if we're testing both the moves A→B and A→C, then it's unnecessary to test A→B→C or A→C→B, since they can't result in shorter paths.
Wrong again:
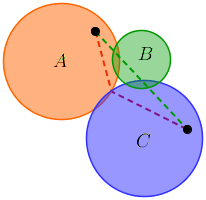
The point is that using purely adjacency-based arguments is not going to cut it; we have to use the geometry of the problem as well.
What the two above examples have in common (as well as the second test-case on a larger scale,) is that there's a "hole" in the enclosed area.
It manifests itself in the fact that some of the points-of-intersection on the boundary—our "nails"—are within the triangle △ABC whose vertices are the circles' centers:
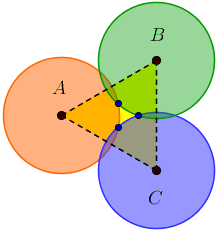
When this happens, there's a chance that going from A to B and from A to C will result in different paths.
More importantly, when it doesn't happen (i.e. if there wasn't a gap between A, B and C) then it's guaranteed that all paths starting with A→B→C and with A→C and which are otherwise equivalent will result in the same locally minimal path, hence if we visit B we don't need to also visit C directly from A.
This leads us to our elimination method:
When we're at a circle A, we keep a list H of the adjacent circles we've visited.
This list is initially empty.
We visit an adjacent circle B if there are any "nails" in all the triangles formed by the centers of A, B and any of the circles in H adjacent to B.
This method dramatically drops the number of paths we have to test to just 1 in the first test-case and 10 in the second one.
A few more notes:
It's possible to decrease the number of paths we test even further, but this method is good enough for the scale of this problem.
I used the algorithm from my solution to the rubber-band challenge.
Since this algorithm is incremental it can be pretty easily integrated into the path-finding process, so that we minimize the path as we go along.
Since many paths share a starting-segment, this can significantly improve performance when we have lots of paths.
It can also hurt performance if there are much more dead-ends than valid paths.
Either way, for the given test-cases performing the algorithm for each path separately is good enough.
There's one edge-case where this solution may fail:
If any of the points on the boundary is the point of intersection of two tangent circles then under some conditions the result can be wrong.
This is due to the way rubber-band algorithm works.
With some modifications it's possible to handle these cases as well, but, hell, it's already long enough.
# First test case
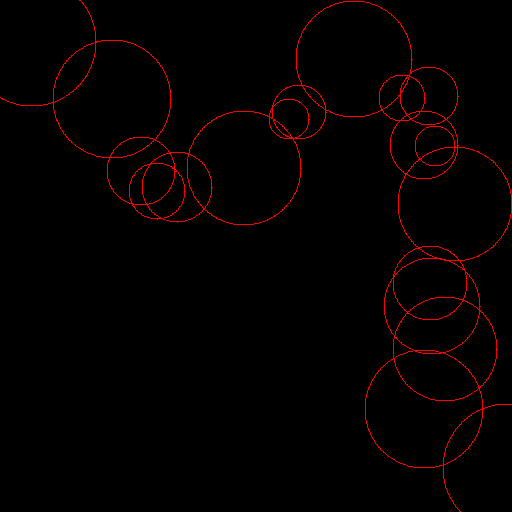
I={((32.,42.),64.),((112.,99.),59.),((141.,171.),34.),((157.,191.),28.),((177.,187.),35.),((244.,168.),57.),((289.,119.),20.),((299.,112.),27.),((354.,59.),58.),((402.,98.),23.),((429.,96.),29.),((424.,145.),34.),((435.,146.),20.),((455.,204.),57.),((430.,283.),37.),((432.,306.),48.),((445.,349.),52.),((424.,409.),59.),((507.,468.),64.)}
# Second test case
#I={((32.,42.),64.),((112.,99.),59.),((141.,171.),34.),((157.,191.),28.),((177.,187.),35.),((244.,168.),57.),((289.,119.),20.),((299.,112.),27.),((354.,59.),58.),((402.,98.),23.),((429.,96.),29.),((424.,145.),34.),((435.,146.),20.),((455.,204.),57.),((430.,283.),37.),((432.,306.),48.),((445.,349.),52.),((424.,409.),59.),((507.,468.),64.),((180.,230.),39.),((162.,231.),39.),((157.,281.),23.),((189.,301.),53.),((216.,308.),27.),((213.,317.),35.),((219.,362.),61.),((242.,365.),42.),((288.,374.),64.),((314.,390.),53.),((378.,377.),30.),((393.,386.),34.)}
from numpy import*
V=array;X=lambda u,v:u[0]*v[1]-u[1]*v[0];L=lambda v:dot(v,v)
e=V([511]*2)
N=set()
for c,r in I:
for C,R in I:
v=V(C)-c;d=L(v)
if d:
a=(r*r-R*R+d)/2/d;q=r*r/d-a*a
if q>=0:w=V(c)+a*v;W=V([-v[1],v[0]])*q**.5;N|={tuple(t)for t in[w+W,w-W]if all([L(t-T)>=s**2-1e-9 for T,s in I])}
N=map(V,N)
def T(a,b,c,p):H=[X(p-a,b-a),X(p-b,c-b),X(p-c,a-c)];return min(H)*max(H)>=0
def E(a,c,b):
try:d=max((X(n-a,b-a)**2,id(n),n)for n in N if T(a,b,c,n)*X(n-b,c-b)*X(n-c,a-c))[2];A=E(a,c,d);B=E(d,c,b);return[A[0]+[d]+B[0],A[1]+[sign(X(c-a,b-c))]+B[1]]
except:return[[]]*2
def P(I,c,r,A):
H=[];M=[""]
if L(c-e)>r*r:
for C,R in I:
if L(C-c)<=L(r+R)and all([L(h-C)>L(R+s)or any([T(c,C,h,p)for p in N])for h,s in H]):v=V(C);H+=[(v,R)];M=min(M,P(I-{(C,R)},v,R,A+[v]))
return M
A+=[e]*2;W=[.5]*len(A)
try:
while 1:
i=[w%1*2or w==0for w in W[2:-2]].index(1);u,a,c,b,v=A[i:i+5];A[i+2:i+3],W[i+2:i+3]=t,_=E(a,c,b);t=[a]+t+[b]
for p,q,j,k in(u,a,1,i+1),(v,b,-2,i+len(t)):x=X(q-p,c-q);y=X(q-p,t[j]-q);z=X(c-q,t[j]-q);d=sign(j*z);W[k]+=(x*y<=0)*(x*z<0 or y*z>0)*(x!=0 or d*W[k]<=0)*(y!=0 or d*W[k]>=0)*d
except:return[sum(L(A[i+1]-A[i])**.5for i in range(len(A)-1)),id(A),A]
print V(P(I,e*0,0,[e*0]*2)[2][1:-1])
Input is given through the variable I as a set of tuples ((x, y), r) where (x, y) is the center of the circle and r is its radius.
The values must be floats, not ints.
The result is printed to STDOUT.
Example
# First test case
I={((32.,42.),64.),((112.,99.),59.),((141.,171.),34.),((157.,191.),28.),((177.,187.),35.),((244.,168.),57.),((289.,119.),20.),((299.,112.),27.),((354.,59.),58.),((402.,98.),23.),((429.,96.),29.),((424.,145.),34.),((435.,146.),20.),((455.,204.),57.),((430.,283.),37.),((432.,306.),48.),((445.,349.),52.),((424.,409.),59.),((507.,468.),64.)}
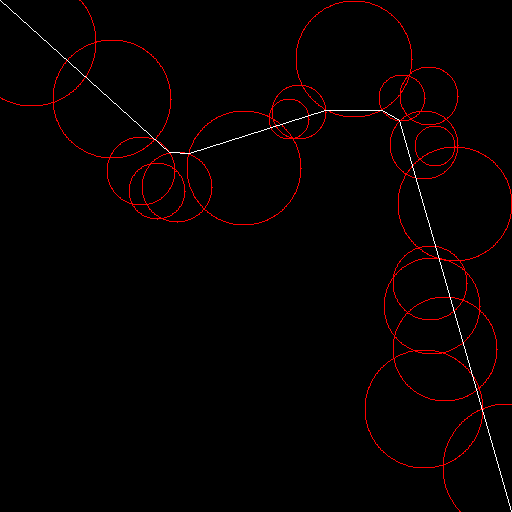
[[ 0. 0. ]
[ 154.58723733 139.8329183 ]
[ 169.69950891 152.76985495]
[ 188.7391093 154.02738541]
[ 325.90536774 109.74141936]
[ 382.19108518 109.68789517]
[ 400.00362897 120.91319495]
[ 511. 511. ]]






2Is the finish suppose to be 511,511? – MickyT – 2014-10-28T02:46:56.517
2How accurate do the intermediate points have to be? Must they be integers? – Keith Randall – 2014-10-28T03:10:58.310
6If I were really so rich, I'd build a tower at (127, 127) with radius 182 with a little tunnel to drive right through. – Anti Earth – 2014-10-28T05:57:59.660
1not consistent: is the destination 255,255 or 511,511? – edc65 – 2014-10-28T07:20:06.517
2
I think after some preparation it should be possible to reduce this problem to this challenge. You might want to add an example that has several paths of towers though.
– Martin Ender – 2014-10-28T07:47:27.373@KeithRandall integers is fine, and accurate enough to be 1-2 units within my answer. I've updated the post. – stokastic – 2014-10-28T12:31:58.803
@edc65 I fixed the specs, the destination should be 511,511. – stokastic – 2014-10-28T12:32:18.623
I will add some more examples later today/tonight. – stokastic – 2014-10-28T12:38:33.090
Can we assume that a valid path exists and that the input isn’t otherwise malformed? – Wrzlprmft – 2014-10-28T14:02:39.460
@Wrzlprmft Yes, input will always have a valid solution. – stokastic – 2014-10-28T14:18:55.443
@MartinBüttner Added a second test case with mutiple routes. – stokastic – 2014-10-28T15:36:15.357
The output to the first test-case is missing a point. See the point of intersection between the second and third circles where it looks like the line passes straight through it? It actually makes ~2° turn there; it should be part of the path. – Ell – 2014-10-30T02:13:26.763