28
5
Given three mutually tangent circles, we can always find two more circles which are tangent to all three of those. These two are called Apollonian circles. Note that one of the Apollonian circles might actually be around the three initial circles.
Starting from three tangent circles, we can create a fractal called an Apollonian gasket, by the following process:
- Call the initial 3 circles the parent circles
- Find the parent circles' two Apollonian circles
- For each Apollonian circle:
- For each pair of the three pairs of parent circles:
- Call the Apollonian circle and the two parent circles the new set of parent circles and start over from step 2.
- For each pair of the three pairs of parent circles:
E.g. starting with circles of equal size, we get:
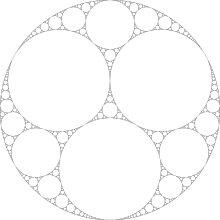
Image found on Wikipedia
There's one more bit of notation we need. If we have a circle of radius r with centre (x, y), we can define it's curvature as k = ±1/r. Usually k will be positive, but we can use negative k to denote the circle that encloses all the other circles in the gasket (i.e. all tangents touch that circle from the inside). Then we can specify a circle with a triplet of numbers: (k, x*k, y*k).
For the purpose of this question, we will assume positive integer k and rational x and y.
Further examples for such circles can be found in the Wikipedia article.
There's also some interesting stuff about integral gaskets in this article (among other fun things with circles).
The Challenge
You will be given 4 circle specifications, each of which will look like (14, 28/35, -112/105). You can use any list format and division operator that is convenient, such that you can simply eval the input if you wish to. You may assume that the 4 circles are indeed tangent to each other, and that the first of them has negative curvature. That means you are already given the surrounding Apollonian circle of the other three. For a list of valid example inputs, see the bottom of the challenge.
Write a program or function which, given this input, draws an Apollonian gasket.
You may take input via function argument, ARGV or STDIN and either render the fractal on screen or write it to an image file in a format of your choice.
If the resulting image is rasterised, it must be at least 400 pixels on each side, with less than 20% padding around the largest circle. You may stop recursing when you reach circles whose radius is less than a 400th of the largest input circle, or circles which are smaller than a pixel, whichever happens first.
You must draw only circle outlines, not full discs, but the colours of background and lines are your choice. The outlines must not be wider than a 200th of the outer circles diameter.
This is code golf, so the shortest answer (in bytes) wins.
Example Inputs
Here are all integral gaskets from the Wikipedia article converted to the prescribed input format:
[[-1, 0, 0], [2, 1, 0], [2, -1, 0], [3, 0, 2]]
[[-2, 0, 0], [3, 1/2, 0], [6, -2, 0], [7, -3/2, 2]]
[[-3, 0, 0], [4, 1/3, 0], [12, -3, 0], [13, -8/3, 2]]
[[-3, 0, 0], [5, 2/3, 0], [8, -4/3, -1], [8, -4/3, 1]]
[[-4, 0, 0], [5, 1/4, 0], [20, -4, 0], [21, -15/4, 2]]
[[-4, 0, 0], [8, 1, 0], [9, -3/4, -1], [9, -3/4, 1]]
[[-5, 0, 0], [6, 1/5, 0], [30, -5, 0], [31, -24/5, 2]]
[[-5, 0, 0], [7, 2/5, 0], [18, -12/5, -1], [18, -12/5, 1]]
[[-6, 0, 0], [7, 1/6, 0], [42, -6, 0], [43, -35/6, 2]]
[[-6, 0, 0], [10, 2/3, 0], [15, -3/2, 0], [19, -5/6, 2]]
[[-6, 0, 0], [11, 5/6, 0], [14, -16/15, -4/5], [15, -9/10, 6/5]]
[[-7, 0, 0], [8, 1/7, 0], [56, -7, 0], [57, -48/7, 2]]
[[-7, 0, 0], [9, 2/7, 0], [32, -24/7, -1], [32, -24/7, 1]]
[[-7, 0, 0], [12, 5/7, 0], [17, -48/35, -2/5], [20, -33/35, 8/5]]
[[-8, 0, 0], [9, 1/8, 0], [72, -8, 0], [73, -63/8, 2]]
[[-8, 0, 0], [12, 1/2, 0], [25, -15/8, -1], [25, -15/8, 1]]
[[-8, 0, 0], [13, 5/8, 0], [21, -63/40, -2/5], [24, -6/5, 8/5]]
[[-9, 0, 0], [10, 1/9, 0], [90, -9, 0], [91, -80/9, 2]]
[[-9, 0, 0], [11, 2/9, 0], [50, -40/9, -1], [50, -40/9, 1]]
[[-9, 0, 0], [14, 5/9, 0], [26, -77/45, -4/5], [27, -8/5, 6/5]]
[[-9, 0, 0], [18, 1, 0], [19, -8/9, -2/3], [22, -5/9, 4/3]]
[[-10, 0, 0], [11, 1/10, 0], [110, -10, 0], [111, -99/10, 2]]
[[-10, 0, 0], [14, 2/5, 0], [35, -5/2, 0], [39, -21/10, 2]]
[[-10, 0, 0], [18, 4/5, 0], [23, -6/5, -1/2], [27, -4/5, 3/2]]
[[-11, 0, 0], [12, 1/11, 0], [132, -11, 0], [133, -120/11, 2]]
[[-11, 0, 0], [13, 2/11, 0], [72, -60/11, -1], [72, -60/11, 1]]
[[-11, 0, 0], [16, 5/11, 0], [36, -117/55, -4/5], [37, -112/55, 6/5]]
[[-11, 0, 0], [21, 10/11, 0], [24, -56/55, -3/5], [28, -36/55, 7/5]]
[[-12, 0, 0], [13, 1/12, 0], [156, -12, 0], [157, -143/12, 2]]
[[-12, 0, 0], [16, 1/3, 0], [49, -35/12, -1], [49, -35/12, 1]]
[[-12, 0, 0], [17, 5/12, 0], [41, -143/60, -2/5], [44, -32/15, 8/5]]
[[-12, 0, 0], [21, 3/4, 0], [28, -4/3, 0], [37, -7/12, 2]]
[[-12, 0, 0], [21, 3/4, 0], [29, -5/4, -2/3], [32, -1, 4/3]]
[[-12, 0, 0], [25, 13/12, 0], [25, -119/156, -10/13], [28, -20/39, 16/13]]
[[-13, 0, 0], [14, 1/13, 0], [182, -13, 0], [183, -168/13, 2]]
[[-13, 0, 0], [15, 2/13, 0], [98, -84/13, -1], [98, -84/13, 1]]
[[-13, 0, 0], [18, 5/13, 0], [47, -168/65, -2/5], [50, -153/65, 8/5]]
[[-13, 0, 0], [23, 10/13, 0], [30, -84/65, -1/5], [38, -44/65, 9/5]]
[[-14, 0, 0], [15, 1/14, 0], [210, -14, 0], [211, -195/14, 2]]
[[-14, 0, 0], [18, 2/7, 0], [63, -7/2, 0], [67, -45/14, 2]]
[[-14, 0, 0], [19, 5/14, 0], [54, -96/35, -4/5], [55, -187/70, 6/5]]
[[-14, 0, 0], [22, 4/7, 0], [39, -12/7, -1/2], [43, -10/7, 3/2]]
[[-14, 0, 0], [27, 13/14, 0], [31, -171/182, -10/13], [34, -66/91, 16/13]]
[[-15, 0, 0], [16, 1/15, 0], [240, -15, 0], [241, -224/15, 2]]
[[-15, 0, 0], [17, 2/15, 0], [128, -112/15, -1], [128, -112/15, 1]]
[[-15, 0, 0], [24, 3/5, 0], [40, -5/3, 0], [49, -16/15, 2]]
[[-15, 0, 0], [24, 3/5, 0], [41, -8/5, -2/3], [44, -7/5, 4/3]]
[[-15, 0, 0], [28, 13/15, 0], [33, -72/65, -6/13], [40, -25/39, 20/13]]
[[-15, 0, 0], [32, 17/15, 0], [32, -161/255, -16/17], [33, -48/85, 18/17]]
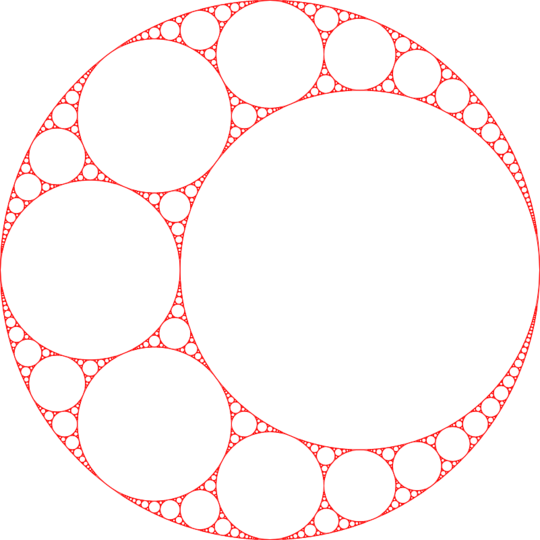



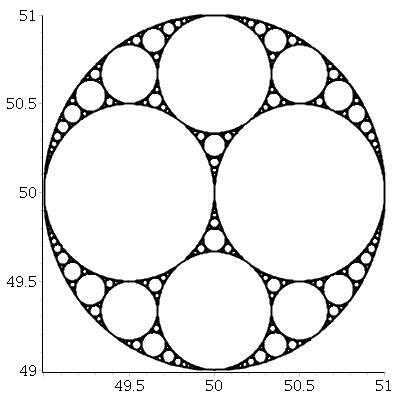
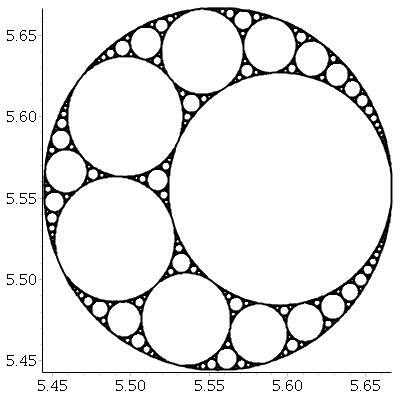
Your example illustration seems to have only included the "inside" apollonian circles after the first operation. – Sparr – 2014-10-08T20:48:18.060
@Sparr I'm not sure what you mean. After the first operation, one of the two Apollonian circles already exists (the original parent circle that you didn't pick for the current iteration) and you're only looking for the other solution. – Martin Ender – 2014-10-08T20:52:45.213
Never mind, you're right, I was mis-reading. – Sparr – 2014-10-08T23:37:09.000