Play the Chaos Game

Question

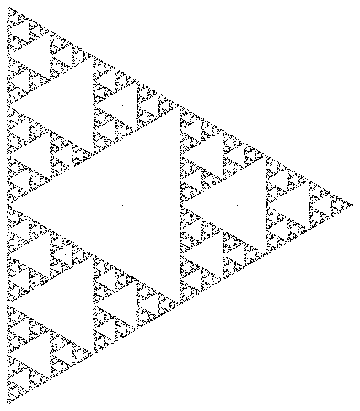
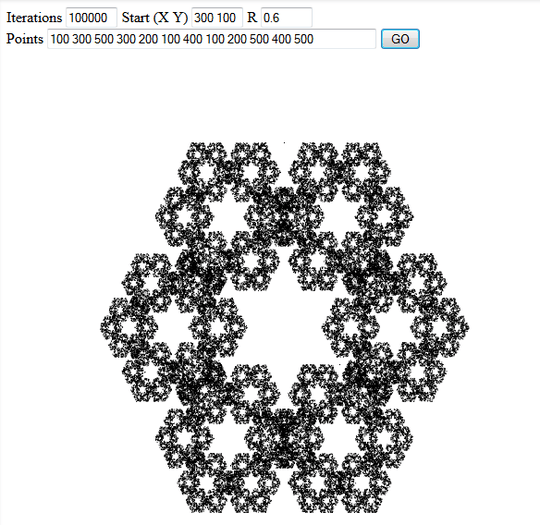
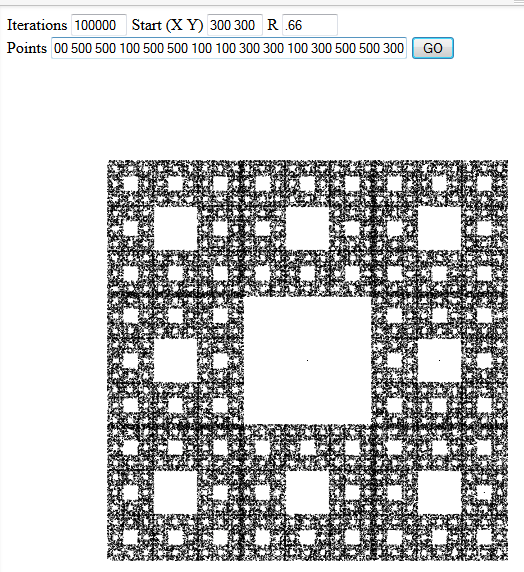
The Chaos Game is a simple method to generate fractals. Given a starting point, a length ratio r and a set of 2D points, repeatedly do the following:

• From your set of points, pick one at random (uniformly).
• Average that point and the last drawn point (or the starting point) using r and 1 - r as the weights (i.e. r = 0 means you get the starting point, r = 1 means you get the random point and r = 0.5 means you get the point halfway in between.)
• Draw the resultant point.

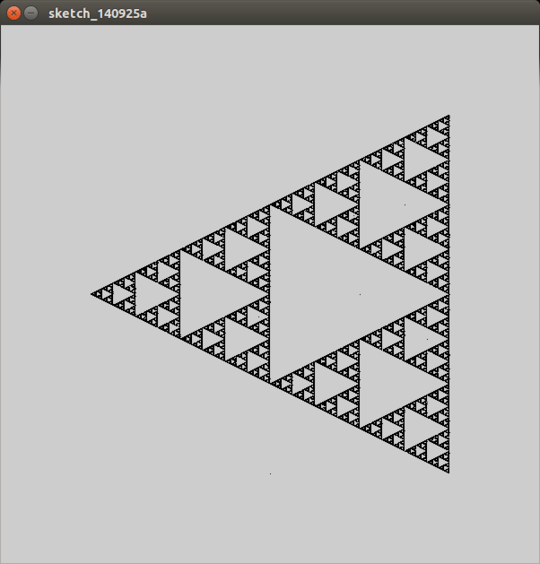
For instance, if you picked the vertices of an equilateral triangle and r = 0.5, the plotted points would map out a Sierpinski triangle:

^{Image found on Wikipedia}

You're to write a program or function which "plays" the chaos game to create a fractal.

Input

You may write either a program or a function, and take following inputs via ARGV, STDIN or function argument:

• The number of points to plot.
• The starting coordinate (which has to be plotted, too!).
• The averaging weight r in the interval [0,1].
• A list of points to choose from.

Output

You may render on screen or write an image file. If the result is rasterised, it needs to be at least 600 pixels on each side, all points must be on the canvas, and at least 75% of the horizontal and vertical extent of the image must be used for points (this is to avoid answers with a single black pixels saying "it's really far zoomed out"). The x and y axis must be on the same scale (that is the line from (0,0) to (1,1) must be at a 45 degree angle) and each point plotted in the chaos game must be represented as a single pixel (if your plotting method anti-aliases the point, it may be spread over 2x2 pixels).

Colours are your choice, but you need at least two distinguishable colours: one for the background and one for the dots plotted during the chaos game. You may but don't have to plot the input points.

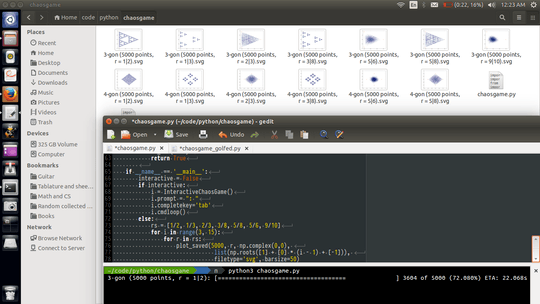
Please include three interesting example outputs in your answer.

Scoring

This is code golf, so the shortest answer (in bytes) wins.

Edit: You no longer need to plot the input points, as they aren't really visible as single pixels anyway.

Answer 1

Mathematica, 89

f[n_,s_,r_,p_]:=Graphics@{AbsolutePointSize@1,Point@NestList[#-r#+r RandomChoice@p&,s,n]}

f[10000, {0, 0}, .5, {{-(1/2), Sqrt[3]/2}, {-(1/2), -(Sqrt[3]/2)}, {1, 0}}]

How it works

In Mathematica the Graphics[] function produces scalable graphics, you render it to whatever size you want by simply dragging the picture corners. In fact, the initial size of all displayed graphics is a ".ini" setting that you may set at 600 or at any other value you wish. So there is no need to do anything special for the 600x600 requirement.

The AbsolutePointSize[] thing specifies that the point size will not be modified by enlarging the image size.

The core construct is

 NestList[#-r#+r RandomChoice@p&,s,n]

or in non-golfed pseudo-code:

 NestList[(previous point)*(1-r) + (random vertex point)*(r), (start point), (iterations)]

It is recursively building a list starting from (start point) and applying the (vectorial) function in the first argument to each successive point, finally returning the list of all calculated points to be plotted by Point[]

Some self-replication examples:

Grid@Partition[Table[
   pts = N@{Re@#, Im@#} & /@ Table[E^(2 I Pi r/n), {r, 0, n - 1}];
   Framed@f[10000, {0, 0}, 1/n^(1/n), pts], {n, 3, 11}], 3]

Answer 2

Java : 246 253 447

As a function m():

void m(float[]a){new java.awt.Frame(){public void paint(java.awt.Graphics g){int i=0,x=i,y=i,v;for(setSize(832,864),x+=a[1],y+=a[2];i++<=a[0];v=a.length/2-2,v*=Math.random(),x+=(a[v+=v+4]-x)*a[3],y+=(a[v+1]-y)*a[3])g.drawLine(x,y,x,y);}}.show();}

Line breaks (within a program to show usage):

class P{
    public static void main(String[]a){
        new P().m(new float[]{1000000,            // iterations
                              416,432,            // start
                              0.6f,               // r
                              416,32,16,432,      // point list...
                              416,832,816,432,
                              366,382,366,482,
                              466,382,466,482});
    }

    void m(float[]a){
        new java.awt.Frame(){
            public void paint(java.awt.Graphics g){
                int i=0,x=i,y=i,v;
                for(setSize(832,864),x+=a[1],y+=a[2];
                    i++<=a[0];
                    v=a.length/2-2,v*=Math.random(),
                    x+=(a[v+=v+4]-x)*a[3],
                    y+=(a[v+1]-y)*a[3])
                    g.drawLine(x,y,x,y);
            }
        }.show();
    }
}

Drawing input points was removed from the requirements (yay 80 bytes!). They're still shown in the old screenshots below, but won't show up if you run it. See revision history if interested.

The inputs are given as an array of floats. The first is iterations, the next two are starting x y. Fourth is r, and last comes the list of coordinates, in x1 y1 x2 y2 ... fashion.

Ninja Star

1000000 400 400 0.6 400 0 0 400 400 800 800 400 350 350 350 450 450 350 450 450

Cross

1000000 400 400 0.8 300 0 500 0 500 300 800 300 800 500 500 500 500 800 300 800 300 500 0 500 0 300 300 300

Octochains

1000000 400 400 0.75 200 0 600 0 800 200 800 600 600 800 200 800 0 600 0 200

Answer 3

JavaScript (E6) + Html 173 176 193

Edit: big cut, thanks to William Barbosa

Edit: 3 bytes less, thanks to DocMax

173 bytes counting the function and the canvas element needed to show the output.

Test save as html file and open in FireFox.

JSFiddle

---

---

---

---

<canvas id=C>
<script>
F=(n,x,y,r,p)=>{
  for(t=C.getContext("2d"),C.width=C.height=600;n--;x-=(x-p[i])*r,y-=(y-p[i+1])*r)
    i=Math.random(t.fillRect(x,y,1,1))*p.length&~1      
}
F(100000, 300, 300, 0.66, [100,500, 500,100, 500,500, 100,100, 300,150, 150,300, 300,450, 450,300]) // Function call, not counted
</script>

Answer 4

Python - 200 189

import os,random as v
def a(n,s,r,z):
    p=[255]*360000
    for i in[1]*(n+1):
        p[600*s[0]+s[1]]=0;k=v.choice(z);s=[int(k[i]*r+s[i]*(1-r))for i in(0,1)]
    os.write(1,b'P5 600 600 255 '+bytes(p))

Takes input as function arguments to a, writes result to stdout as pgm file. n is iterations, s is starting point, r is r, and z is list of input points.

Edit: No longer draws input points in gray.

Interesting outputs:

Iterations: 100000
Starting Point: (200, 200)
r: 0.8
Points: [(0, 0), (0, 599), (599, 0), (599, 599), (300, 300)]

---

Iterations: 100000
Starting Point: (100, 300)
r: 0.6
Points: [(0, 0), (0, 599), (599, 0), (300, 0), (300, 300), (0, 300)]

---

Iterations: 100000
Starting Point: (450, 599)
r: 0.75
Points: [(0, 0), (0, 300), (0, 599), (300, 0), (599, 300), (150, 450)]

Answer 5

Python, 189 183 175

Edit: fixed the inversed r ratio, and switched to B&W image in order to save a few bytes.

Takes the number of points as n, first point as p, ratio as r and list of points as l. Needs the module Pillow.

import random,PIL.Image as I
s=850
def c(n,p,r,l):
    i=I.new('L',(s,s));x,y=p;
    for j in range(n):w,z=random.choice(l);w*=r;z*=r;x,y=x-x*r+w,y-y*r+z;i.load()[x,s-y]=s
    i.show()

Examples:

I am generating points in circle around the image's center

points = [(425+s*cos(a)/2, 425+s*sin(a)/2) for a in frange(.0, 2*pi, pi/2)]
c(1000000, (425, 425), 0.4, points)

XOXO repetitions, just changing ratio from 0.4 to 0.6

Some sort of snow flake

stars = [(425+s*cos(a)/2,425+s*sin(a)/2) for a in frange(.0,2*pi, pi/4)]
c(1000000, (425, 425), 0.6, stars)

Answer 6

SuperCollider - 106

SuperCollider is a language for generating music, but it can do graphics at a pinch.

f={|n,p,r,l|Window().front.drawHook_({{Pen.addRect(Rect(x(p=l.choose*(1-r)+(p*r)),p.y,1,1))}!n;Pen.fill})}

I've used some obscure syntax shortcuts to save a few bytes - a more readable and more memory-efficient version is

f={|n,p,r,l|Window().front.drawHook_({n.do{Pen.addRect(Rect(p.x,p.y,1,1));p=l.choose*(1-r)+(p*r)};Pen.fill})}

at 109 chars.

As with the Mathematica example, you have to manually resize the window to get 600x600 pixels. You have to wait for it to re-draw when you do this.

This generates a basic Sierpinsky triangle (not shown because you've seen it before)

f.(20000,100@100,0.5,[0@600,600@600,300@0])

This makes a kind of Sierpinsky pentagon type thing:

f.(100000,100@100,1-(2/(1+sqrt(5))),{|i| (sin(i*2pi/5)+1*300)@(1-cos(i*2pi/5)*300)}!5)

The same thing with 6 points leaves an inverted Koch snowflake in the middle:

f.(100000,100@100,1/3,{|i| (sin(i*2pi/6)+1*300)@(1-cos(i*2pi/6)*300)}!6)

Finally, here's a riff on the 3D pyramids from ace's answer. (Note that I've used one of the points twice, to get the shading effect.)

f.(150000,100@100,0.49,[300@180, 0@500,0@500,350@400,600@500,250@600])

Answer 7

JavaScript (407) (190)

I'm happy to get any feedback on my script and on golfing since I am not comfortable with JS=) (Feel free to use this/change it for your own submission!)

Reading Input (To be comparable to edc65's entry I do not count the the input.):

p=prompt;n=p();[x,y]=p().split(',');r=p();l=p().split(';').map(e=>e.split(','));

Canvas Setup & Calculation

d=document;d.body.appendChild(c=d.createElement('canvas'));c.width=c.height=1000;c=c.getContext('2d');
for(;n--;c.fillRect(x,y,2,2),[e,f]= l[Math.random()*l.length|0],x-=x*r-e*r,y-=y*r-f*r);

Somewhat more ungolfed (including an example input where the real input promts are just commented out, so ready to use):

p=prompt;
n=p('n','4000');
[x,y]=p('start','1,1').split(',');
r=p('r','0.5');
l=p('list','1,300;300,1;300,600;600,300').split(';').map(e=>e.split(','));d=document;
d.body.appendChild(c=d.createElement('canvas'));
c.width=c.height=1000;c=c.getContext('2d');
for(;n--;c.fillRect(x,y,2,2),[e,f]= l[Math.random()*l.length|0],x-=x*r-e*r,y-=y*r-f*r);

Examples

for(k = 0; k<50; k++){
rad = 10;
l.push([350+rad*k*Math.cos(6.28*k/10),350+rad*k*Math.sin(6.28*k/10)]);
}
r = 1.13;

r = 0.5;list = [[1,1],[300,522],[600,1],[300,177]];

r = 0.5
list = [[350+350*Math.sin(6.28*1/5),350+350*Math.cos(6.28*1/5)],
[350+350*Math.sin(6.28*2/5),350+350*Math.cos(6.28*2/5)],
[350+350*Math.sin(6.28*3/5),350+350*Math.cos(6.28*3/5)],
[350+350*Math.sin(6.28*4/5),350+350*Math.cos(6.28*4/5)],
[350+350*Math.sin(6.28*5/5),350+350*Math.cos(6.28*5/5)],


[350+90*Math.sin(6.28*1.5/5),350+90*Math.cos(6.28*1.5/5)],
[350+90*Math.sin(6.28*2.5/5),350+90*Math.cos(6.28*2.5/5)],
[350+90*Math.sin(6.28*3.5/5),350+90*Math.cos(6.28*3.5/5)],
[350+90*Math.sin(6.28*4.5/5),350+90*Math.cos(6.28*4.5/5)],
[350+90*Math.sin(6.28*5.5/5),350+90*Math.cos(6.28*5.5/5)]];

Answer 8

Processing, 153

Ported @Geobits' Java answer to Processing and did some more golfing, resulting in a reduction of 100 chars. I originally intended to animate the process, but the input constraints are too harsh on this (Processing does not have stdin or argv, which means that I must write my own function instead of using Processing's native draw() loop).

void d(float[]a){int v;size(600,600);for(float i=0,x=a[1],y=a[2];i++<a[0];v=(int)random(a.length/2-2),point(x+=(a[v*2+4]-x)*a[3],y+=(a[v*2+5]-y)*a[3]));}

Complete program with line breaks:

void setup() {
  d(new float[]{100000,300,300,.7,0,600,600,0,600,600,0,0,400,400,200,200,400,200,200,400}); 
}
void d(float[]a){
  int v;
  size(600,600);
  for(float i=0,x=a[1],y=a[2];
      i++<a[0];
      v=(int)random(a.length/2-2),point(x+=(a[v*2+4]-x)*a[3],y+=(a[v*2+5]-y)*a[3]));
}

Above program gives Crosses:

d(new float[]{100000,300,300,.65,142,257,112,358,256,512,216,36,547,234,180,360}); 

This gives Pyramids:

d(new float[]{100000,100,500,.5,100,300,500,100,500,500});

This gives Sierpinski triangle:

Answer 9

Ungolfed "reference implementation", Python

Update: much, much faster (by orders of magnitude)

Check out the interactive shell!

Edit the file and set interactive to True, then do one of these:

polygon numberOfPoints numeratorOfWeight denominatorOfWeight startX startY numberOfSides generates, saves and displays a polygon.

points numberOfPoints numeratorOfWeight denominatorOfWeight startX startY point1X point1Y point2X point2Y ... does what the spec asks for.

import matplotlib.pyplot as plt
import numpy as np
from fractions import Fraction as F
import random
from matplotlib.colors import ColorConverter
from time import sleep
import math
import sys
import cmd
import time

def plot_saved(n, r, start, points, filetype='png', barsize=30, dpi=100, poly=True, show=False):
    printed_len = 0

    plt.figure(figsize=(6,6))
    plt.axis('off')

    start_time = time.clock()
    f = F.from_float(r).limit_denominator()

    spts = []
    for i in range(len(points)):
        spts.append(tuple([round(points[i].real,1), round(points[i].imag,1)]))

    if poly:
        s = "{}-gon ({}, r = {}|{})".format(len(points), n, f.numerator, f.denominator)
    else:
        s = "{} ({}, r = {}|{})".format(spts, n, f.numerator, f.denominator) 

    step = math.floor(n / 50)

    for i in range(len(points)):
        plt.scatter(points[i].real, points[i].imag, color='#ff2222', s=50, alpha=0.7)

    point = start
    t = time.clock()

    xs = []
    ys = []

    for i in range(n+1):
        elapsed = time.clock() - t
        #Extrapolation
        eta = (n+1-i)*(elapsed/(i+1))
        printed_len = rewrite("{:>29}: {} of {} ({:.3f}%) ETA: {:.3f}s".format(
                s, i, n, i*100/n, eta), printed_len)
        xs.append(point.real)
        ys.append(point.imag)
        point = point * r + random.choice(points) * (1 - r)

    printed_len = rewrite("{:>29}: plotting...".format(s), printed_len)
    plt.scatter(xs, ys, s=0.5, marker=',', alpha=0.3)

    presave = time.clock()
    printed_len = rewrite("{:>29}: saving...".format(s), printed_len)
    plt.savefig(s + "." + filetype, bbox_inches='tight', dpi=dpi)

    postsave = time.clock()
    printed_len = rewrite("{:>29}: done in {:.3f}s (save took {:.3f}s)".format(
                            s, postsave - start_time, postsave - presave),
                            printed_len)

    if show:
        plt.show()
    print()
    plt.clf()

def rewrite(s, prev):
    spaces = prev - len(s)
    sys.stdout.write('\r')
    sys.stdout.write(s + ' '*(0 if spaces < 0 else spaces))
    sys.stdout.flush()
    return len(s)

class InteractiveChaosGame(cmd.Cmd):
    def do_polygon(self, args):
        (n, num, den, sx, sy, deg) = map(int, args.split())
        plot_saved(n, (num + 0.0)/den, np.complex(sx, sy), list(np.roots([1] + [0]*(deg - 1) + [-1])), show=True)

    def do_points(self, args):
        l = list(map(int, args.split()))
        (n, num, den, sx, sy) = tuple(l[:5])
        l = l[5:]
        points = []
        for i in range(len(l)//2):
            points.append(complex(*tuple([l[2*i], l[2*i + 1]])))
        plot_saved(n, (num + 0.0)/den, np.complex(sx, sy), points, poly=False, show=True)

    def do_pointsdpi(self, args):
        l = list(map(int, args.split()))
        (dpi, n, num, den, sx, sy) = tuple(l[:6])
        l = l[6:]
        points = []
        for i in range(len(l)//2):
            points.append(complex(*tuple([l[2*i], l[2*i + 1]])))
        plot_saved(n, (num + 0.0)/den, np.complex(sx, sy), points, poly=False, show=True, dpi=dpi)

    def do_default(self, args):
        do_generate(self, args)

    def do_EOF(self):
        return True

if __name__ == '__main__':
    interactive = False
    if interactive:
        i = InteractiveChaosGame()
        i.prompt = ": "
        i.completekey='tab'
        i.cmdloop()
    else:
        rs = [1/2, 1/3, 2/3, 3/8, 5/8, 5/6, 9/10]
        for i in range(3, 15):
            for r in rs:
                plot_saved(20000, r, np.complex(0,0), 
                            list(np.roots([1] + [0] * (i - 1) + [-1])), 
                            filetype='png', dpi=300)

Answer 10

Python (202 chars)

Takes the number of points as n, the averaging weight as r, the starting point as a tuple s and the list of points as a list of XY tuples called l.

import random as v,matplotlib.pyplot as p
def t(n,r,s,l):
 q=complex;s=q(*s);l=[q(*i)for i in l];p.figure(figsize=(6,6))
 for i in range(n):p.scatter(s.real,s.imag,s=1,marker=',');s=s*r+v.choice(l)*(1-r)
 p.show()