56
7
Little Chandler is sad. Draw him a cloud to cheer him up.
Note: Drawing a cloud won't actually cheer him up.
A circle can be defined as a 3-tuple (x,y,r) where x is the x position of the circle on a Cartesian plane, y is the y position of the circle on a Cartesian plane, and r is the radius of the circle. x and y may be negative. r is always positive. The input is a list of circles in the form of space separated 3-tuples. For instance:
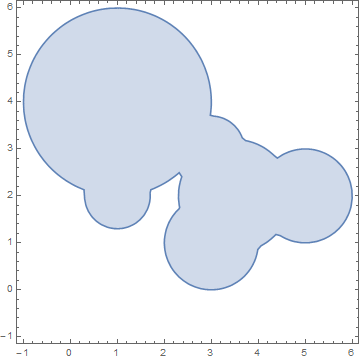
3,1,1 3,2,1.5 1,2,0.7 0.9,1.2,1.2 1,0,0.8
The 3,1,1 means "A circle with centre point at 3,1 with 1 radius. 3,2,1.5 means "A circle with centre point at 3,2 with 1.5 radius.
If we draw all of these circles of the input on a graph, it looks like this (I've included grid lines and labels for clarity only; they are not required):
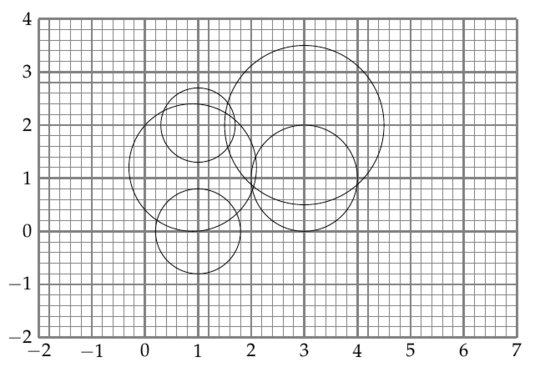
Notice how all the circles are cohesive. That is, they're all overlapped together such that it forms one large group without any small groups of circles separated from the rest. The input is guaranteed to be cohesive.
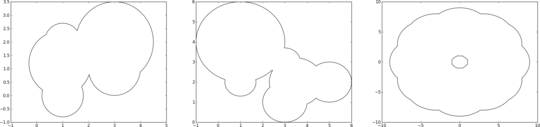
Suppose now we draw a line that travels around the "border" formed by these circles, without any of the other lines. It would be like drawing the border of the silhouette formed by all the circles. The resulting cloud would look something like this:
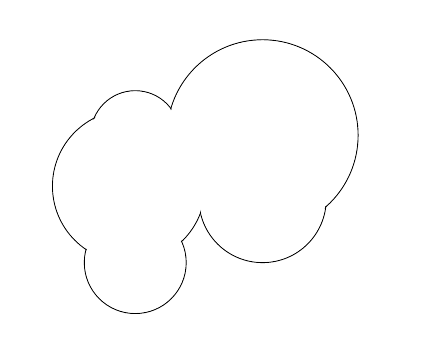
So this cloud has been formed by drawing only the arcs of the circles in the input that form a border, resulting in a single shape. In other words, the cloud is formed by only drawing the arcs that are not within another circle. Your program will take in input in the form explained above, and output an image that displays the resulting cloud. The overall shape of the cloud must be correct, but the scale, colour, line thickness, and how it looks at vertexes is up to you. Note that the cloud must be visible, so you can't pull something like "This program draws a white cloud on a white background", "This program draws a cloud at a infinitesimally small scale", "This program draws a cloud with 0 line thickness", etc. Also note that the colour of the border must be different from the colour of the fill or background.
Another example. Input:
1,4,2 5,2,1 3,1,1 3.5,2,1.2 3,3,0.7 1,2,0.7
Output:

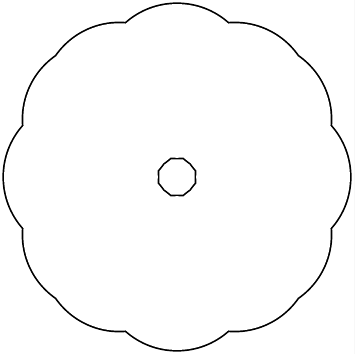
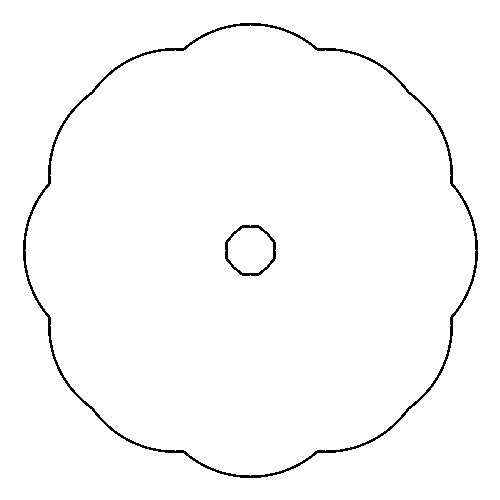
If there is a "hole" in the cloud, you should draw the hole as well. Input:
0,5,4 3,4,4 4,3,4 5,0,4 4,-3,4 3,-4,4 0,-5,4 -3,-4,4 -4,-3,4 -5,0,4 -4,3,4 -3,4,4
Output:
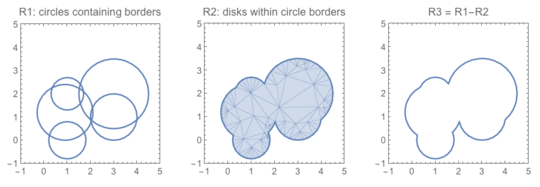
Here is an important rule: your program must draw only the lines that form the border. This means that you CANNOT simply draw the circles fully, and then draw the circles slightly smaller with a white fill -- because that method still draws lines that don't form a border, it just covers them up afterwards. The purpose of the rule was to prevent the "draw the circles, then draw the circles again with a white fill" implementations, or anything similar to that. The answer is expected to actually calculate where to draw things before drawing it.
This is code golf, so the shortest character count wins.




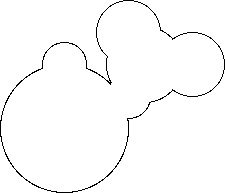
13+1 for an graphical-output question with an objective winning criterion (and the first paragraph). – Dennis – 2014-09-23T03:57:50.373
2How can you tell if we draw a line and erase it afterwards? Is rendering said lines onto internal bitmaps OK? If not, where is the border, between a vector and a bitmap representation? If yes, why not let us do the same with the primary canvas (that we know is double-buffered, so that the user can't see our temporary lines)? – John Dvorak – 2014-09-23T04:03:02.043
1@JanDvorak The purpose of the rule was to prevent the "draw the circles, then draw the circles again with a white fill" implementations, or anything similiar to that. The answer is expected to actually calculate where to draw things before drawing it. I'll edit to make it more clear. – absinthe – 2014-09-23T04:05:59.760
When you say the colour of the cloud is up to us, does that include the interior or only the outline? Also what about axes? Do we need to omit those? – Martin Ender – 2014-09-23T10:06:18.243
Does it have to be a full program, or a functions allowed? – Martin Ender – 2014-09-23T11:23:43.540
@MartinBüttner You may omit axes. Both the interior and the outline may be whatever colour you choose. Functions are not allowed - I use the diction "your program" in the question. – absinthe – 2014-09-23T12:07:24.323
1@Lilac I doubt it would win a code golf, but would drawing the circles against a background of a different colour, and then performing edge detection be allowed? It only draws the circles once, and that is an intermediate stage that allows the line drawing function to create a new image as the output. Does this count as similar to the 2x circles method? – Baldrickk – 2014-09-23T12:46:26.870
1In the last example there is a radius -4. A typo? – edc65 – 2014-09-23T13:20:15.447
15
This question is absolutely hilarious with Cloud to Butt (https://chrome.google.com/webstore/detail/cloud-to-butt-plus/apmlngnhgbnjpajelfkmabhkfapgnoai?hl=en) installed.
– Erty Seidohl – 2014-09-23T14:25:28.537Can I "output" a svg file ? – user80551 – 2014-09-23T15:11:01.033
1@Erty I've got that! I read through the example and was thinking "That doesn't look like a butt at all..." – SomeKittens – 2014-09-23T20:44:58.360
@edc65 That's a typo, yes. It's supposed to be 4. Will edit. – absinthe – 2014-09-23T20:46:53.383
@user80551 Yes. – absinthe – 2014-09-23T20:48:57.287
9@SomeKittens I lost it at "If there is a "hole" in the cloud, you should draw the hole as well." – Erty Seidohl – 2014-09-23T20:59:34.393
@Baldrickk - That's okay. As long as it's not the drawing circles with a slightly smaller radius method. – absinthe – 2014-09-23T21:01:45.763
By "as long as it's not the drawing circles with a slightly smaller radius method" do you mean that I can make a black background and draw white borderless circles on it? – user12205 – 2014-09-25T20:14:04.010
@ace No. That's not really in the spirit of the question - I'll edit for a new rule to exclude that. – absinthe – 2014-09-25T20:45:22.070
@SomeKittens I was going to say, those are some horribly deformed butts it's drawing! – Doktor J – 2014-09-26T15:33:56.977