Using ~ for NOT and N for NAND, a computer search (without sharing terms between outputs) finds a solution with 82 NANDs without sharing. Manually looking for sharing terms reduces it to 54 NANDs, and a computer search that includes sharing further reduces it to 37 NANDs. The minimum might be even lower, as the method is certainly not exhaustive.
Here's the program that recreates the above table. Each line is labeled with the NANDS for that output.
#include <stdio.h>
int N(int x, int y) { return 1 & ~(x & y); }
void main(void)
{
int i0, i1, i2, i3;
for (i3 = 0; i3 <= 1; i3++) {
for (i2 = 0; i2 <= 1; i2++) {
for (i1 = 0; i1 <= 1; i1++) {
for (i0 = 0; i0 <= 1; i0++) {
printf("%d %d %d %d : %d %d %d %d %d %d %d\n", i3, i2, i1, i0,
/* 14 */ N(N(N(i3, N(i2, i1)), N(N(i2, i0), ~i1)), N(N(i2, N(i3, N(i3, i0))), N(i0, N(i3, N(i3, i1))))),
/* 12 */ N(N(N(i3, i0), N(i2, N(i1, i0))), N(~i1, N(N(i3, i0), N(~i3, N(i2, i0))))),
/* 10 */ N(N(i0, N(i3, i1)), N(N(i3, i2), N(i1, N(i1, N(~i3, ~i2))))),
/* 16 */ N(N(N(i2, i1), N(N(i3, i0), N(i2, i0))), N(N(i0, N(i1, ~i2)), N(N(i3, i2), N(N(i3, i1), N(i2, N(i2, i1)))))),
/* 7 */ N(N(i3, i2), N(N(i2, N(i2, i1)), N(i0, N(i3, i1)))),
/* 11 */ N(N(i3, N(i2, N(i3, i1))), N(N(i1, N(i2, N(i2, i0))), N(i0, N(i2, ~i3)))),
/* 12 */ N(N(i3, i0), ~N(N(i1, N(i2, i0)), N(N(i3, i2), N(~i3, N(i2, N(i2, i1)))))) );
} } } }
}
And here's the output:
0 0 0 0 : 1 1 1 1 1 1 0
0 0 0 1 : 0 1 1 0 0 0 0
0 0 1 0 : 1 1 0 1 1 0 1
0 0 1 1 : 1 1 1 1 0 0 1
0 1 0 0 : 0 1 1 0 0 1 1
0 1 0 1 : 1 0 1 1 0 1 1
0 1 1 0 : 1 0 1 1 1 1 1
0 1 1 1 : 1 1 1 0 0 0 0
1 0 0 0 : 1 1 1 1 1 1 1
1 0 0 1 : 1 1 1 1 0 1 1
1 0 1 0 : 1 1 1 0 1 1 1
1 0 1 1 : 0 0 1 1 1 1 1
1 1 0 0 : 1 0 0 1 1 1 0
1 1 0 1 : 0 1 1 1 1 0 1
1 1 1 0 : 1 0 0 1 1 1 1
1 1 1 1 : 1 0 0 0 1 1 1
And here are the equivalent equations, sharing terms that get it down to 54 NANDs:
/* 1 */ int z1 = 1 - i1;
/* 1 */ int z2 = 1 - i2;
/* 1 */ int z3 = 1 - i3;
/* 1 */ int n_i2_i0 = N(i2, i0);
/* 1 */ int n_i2_i1 = N(i2, i1);
/* 1 */ int n_i3_i0 = N(i3, i0);
/* 1 */ int n_i3_i1 = N(i3, i1);
/* 1 */ int n_i3_i2 = N(i3, i2);
/* 1 */ int n_i0_n_i3_i1 = N(i0, n_i3_i1);
/* 1 */ int n_i2_n_i2_i1 = N(i2, n_i2_i1);
printf("%d %d %d %d : %d %d %d %d %d %d %d\n", i3, i2, i1, i0,
/* 9 */ N(N(N(i3, n_i2_i1), N(n_i2_i0, z1)), N(N(i2, N(i3, n_i3_i0)), N(i0, N(i3, n_i3_i1)))),
/* 7 */ N(N(n_i3_i0, N(i2, N(i1, i0))), N(z1, N(n_i3_i0, N(z3, n_i2_i0)))),
/* 5 */ N(n_i0_n_i3_i1, N(n_i3_i2, N(i1, N(i1, N(z3, z2))))),
/* 8 */ N(N(n_i2_i1, N(n_i3_i0, n_i2_i0)), N(N(i0, N(i1, z2)), N(n_i3_i2, N(n_i3_i1, n_i2_n_i2_i1)))),
/* 2 */ N(n_i3_i2, N(n_i2_n_i2_i1, n_i0_n_i3_i1)),
/* 8 */ N(N(i3, N(i2, n_i3_i1)), N(N(i1, N(i2, n_i2_i0)), N(i0, N(i2, z3)))),
/* 6 */ N(n_i3_i0, ~N(N(i1, n_i2_i0), N(n_i3_i2, N(z3, n_i2_n_i2_i1)))) );
And here's the 37 NAND solution:
x0fff = N(i3, i2);
x33ff = N(i3, i1);
x55ff = N(i3, i0);
x0f0f = not(i2);
x3f3f = N(i2, i1);
x5f5f = N(i2, i0);
xcfcf = N(i2, x3f3f);
xf3f3 = N(i1, x0f0f);
x5d5d = N(i0, xf3f3);
xaaa0 = N(x55ff, x5f5f);
xfc30 = N(x33ff, xcfcf);
xd5df = N(x3f3f, xaaa0);
xf3cf = N(x0fff, xfc30);
xaeb2 = N(x5d5d, xf3cf);
x7b6d = N(xd5df, xaeb2);
xb7b3 = N(i1, x7b6d);
xf55f = N(x0fff, xaaa0);
xcea0 = N(x33ff, xf55f);
x795f = N(xb7b3, xcea0);
xd7ed = N(xaeb2, x795f);
xfaf0 = N(x55ff, x0f0f);
xae92 = N(x55ff, x7b6d);
xdd6d = N(x33ff, xae92);
x279f = N(xfaf0, xdd6d);
xaf0f = N(i2, x55ff);
x50ff = N(i3, xaf0f);
xef4c = N(xb7b3, x50ff);
x1cb3 = N(xf3cf, xef4c);
xef7c = N(xf3cf, x1cb3);
xfb73 = N(i1, x279f);
x2c9e = N(xd7ed, xfb73);
xdf71 = N(xf3cf, x2c9e);
xdd55 = N(i0, x33ff);
xf08e = N(x0fff, xdf71);
x2ffb = N(xdd55, xf08e);
x32ba = N(xcfcf, xdd55);
xfd45 = N(x0fff, x32ba);
printf("%d %d %d %d : %d %d %d %d %d %d %d\n", i3, i2, i1, i0,
xd7ed, x279f, x2ffb, x7b6d, xfd45, xdf71, xef7c);
} } } }
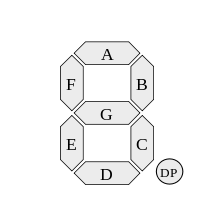


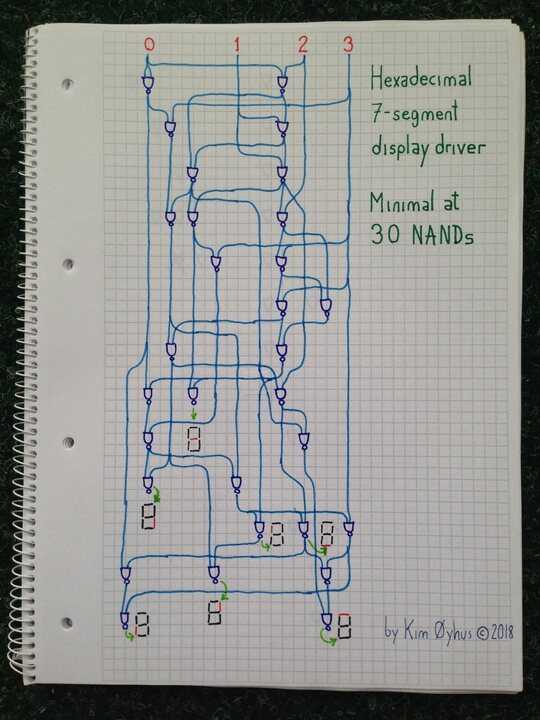
this challenge seems to be about drawing a circuit diagram, and not about coding. Also, the point values per gate seem arbitrary (maybe intentionally), and using AND+NOT is 3 points, when you state NAND is only 1. – stokastic – 2014-09-11T18:32:00.370
@stokastic There are plenty of other [tag:logic-gates] challenges on this site, so I am assuming this category of challenge acceptable to the community. Many use the same scoring system. NAND logic I think explains this scoring system quite well.
– Digital Trauma – 2014-09-11T18:40:07.070Fair enough. I hadn't seen those tags before. It just doesn't seem to really fit in 'programming puzzles' or 'code golf'. – stokastic – 2014-09-11T19:05:15.230
Can the circuit split? In other words, can you save values to variables and recall them later? – xnor – 2014-09-11T19:24:03.043
@xnor Are you talking about this sort of thing: http://codegolf.stackexchange.com/a/26235/11259? If so, the answer is yes.
– Digital Trauma – 2014-09-11T19:37:44.087I assume they have to be 2-input NAND gates (you can't cheat by using NAND gates with more than 2 inputs each.) If you search for previous questions about NAND gates, most of them state this explicitly. – Level River St – 2014-09-11T21:45:50.927
We had to do this in my second year of undergrad engineering. No way am I doing it again for fun. :D :P My answer is: use an FPGA. :D – COTO – 2014-09-11T22:22:34.713
@steveverrill That is correct. I will clarify that. – Digital Trauma – 2014-09-11T23:52:25.120