C++, 275,000,000+
We'll refer to pairs whose magnitude is accurately representable, such as (x, 0), as honest pairs and to all other pairs as dishonest pairs of magnitude m, where m is the pair's wrongly-reported magnitude.
The first program in the previous post used a set of tightly related couples of honest- and dishonest-pairs:
(x, 0) and (x, 1), respectively, for large enough x.
The second program used the same set of dishonest pairs but extended the set of honest pairs by looking for all honest pairs of integral magnitude.
The program doesn't terminate within ten minutes, but it finds the vast majority of its results very early on, which means that most of the runtime goes to waste.
Instead of keep looking for ever-less-frequent honest pairs, this program uses the spare time to do the next logical thing: extending the set of dishonest pairs.
From the previous post we know that for all large-enough integers r, sqrt(r2 + 1) = r, where sqrt is the floating-point square root function.
Our plan of attack is to find pairs P = (x, y) such that x2 + y2 = r2 + 1 for some large-enough integer r.
That's simple enough to do, but naively looking for individual such pairs is too slow to be interesting.
We want to find these pairs in bulk, just like we did for honest pairs in the previous program.
Let {v, w} be an orthonormal pair of vectors.
For all real scalars r, ||r v + w||2 = r2 + 1.
In ℝ2, this is a direct result of the Pythagorean theorem:
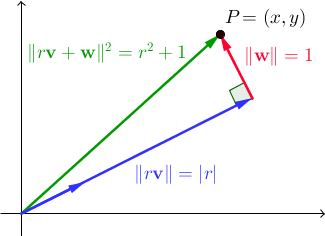
We're looking for vectors v and w such that there exists an integer r for which x and y are also integers.
As a side note, note that the set of dishonest pairs we used in the previous two programs was simply a special case of this, where {v, w} was the standard basis of ℝ2; this time we wish to find a more general solution.
This is where Pythagorean triplets (integers triplets (a, b, c) satisfying a2 + b2 = c2, which we used in the previous program) make their comeback.
Let (a, b, c) be a Pythagorean triplet.
The vectors v = (b/c, a/c) and w = (-a/c, b/c) (and also
w = (a/c, -b/c)) are orthonormal, as is easy to verify.
As it turns out, for any choice of Pythagorean triplet, there exists an integer r such that x and y are integers.
To prove this, and to effectively find r and P, we need a little number/group theory; I'm going to spare the details.
Either way, suppose we have our integral r, x and y.
We're still short of a few things: we need r to be large enough and we want a fast method to derive many more similar pairs from this one.
Fortunately, there's a simple way to accomplish this.
Note that the projection of P onto v is r v, hence r = P · v = (x, y) · (b/c, a/c) = xb/c + ya/c, all this to say that xb + ya = rc.
As a result, for all integers n, (x + bn)2 + (y + an)2 = (x2 + y2) + 2(xb + ya)n + (a2 + b2)n2 = (r2 + 1) + 2(rc)n + (c2)n2 = (r + cn)2 + 1.
In other words, the squared magnitude of pairs of the form
(x + bn, y + an) is (r + cn)2 + 1, which is exactly the kind of pairs we're looking for!
For large enough n, these are dishonest pairs of magnitude r + cn.
It's always nice to look at a concrete example.
If we take the Pythagorean triplet (3, 4, 5), then at r = 2 we have P = (1, 2) (you can check that (1, 2) · (4/5, 3/5) = 2 and, clearly, 12 + 22 = 22 + 1.)
Adding 5 to r and (4, 3) to P takes us to r' = 2 + 5 = 7 and P' = (1 + 4, 2 + 3) = (5, 5).
Lo and behold, 52 + 52 = 72 + 1.
The next coordinates are r'' = 12 and P'' = (9, 8), and again, 92 + 82 = 122 + 1, and so on, and so on ...
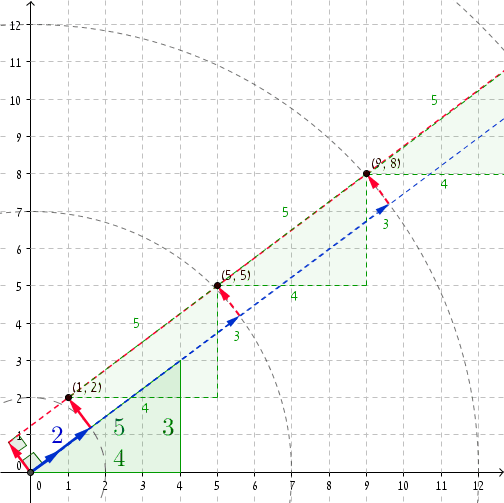
Once r is large enough, we start getting dishonest pairs with magnitude increments of 5.
That's roughly 27,797,402 / 5 dishonest pairs.
So now we have plenty of integral-magnitude dishonest pairs.
We can easily couple them with the honest pairs of the first program to form false-positives, and with due care we can also use the honest pairs of the second program.
This is basically what this program does.
Like the previous program, it too finds most of its results very early on---it gets to 200,000,000 false positives within a few seconds---and then slows down considerably.
Compile with g++ flspos.cpp -oflspos -std=c++11 -msse2 -mfpmath=sse -O3.
To verify the results, add -DVERIFY (this will be notably slower.)
Run with flspos. Any command-line argument for verbose mode.
#include <cstdio>
#define _USE_MATH_DEFINES
#undef __STRICT_ANSI__
#include <cmath>
#include <cfloat>
#include <vector>
#include <iterator>
#include <algorithm>
using namespace std;
/* Make sure we actually work with 64-bit precision */
#if defined(VERIFY) && FLT_EVAL_METHOD != 0 && FLT_EVAL_METHOD != 1
# error "invalid FLT_EVAL_METHOD (did you forget `-msse2 -mfpmath=sse'?)"
#endif
template <typename T> struct widen;
template <> struct widen<int> { typedef long long type; };
template <typename T>
inline typename widen<T>::type mul(T x, T y) {
return typename widen<T>::type(x) * typename widen<T>::type(y);
}
template <typename T> inline T div_ceil(T a, T b) { return (a + b - 1) / b; }
template <typename T> inline typename widen<T>::type sq(T x) { return mul(x, x); }
template <typename T>
T gcd(T a, T b) { while (b) { T t = a; a = b; b = t % b; } return a; }
template <typename T>
inline typename widen<T>::type lcm(T a, T b) { return mul(a, b) / gcd(a, b); }
template <typename T>
T div_mod_n(T a, T b, T n) {
if (b == 0) return a == 0 ? 0 : -1;
const T n_over_b = n / b, n_mod_b = n % b;
for (T m = 0; m < n; m += n_over_b + 1) {
if (a % b == 0) return m + a / b;
a -= b - n_mod_b;
if (a < 0) a += n;
}
return -1;
}
template <typename T> struct pythagorean_triplet { T a, b, c; };
template <typename T>
struct pythagorean_triplet_generator {
typedef pythagorean_triplet<T> result_type;
private:
typedef typename widen<T>::type WT;
result_type p_triplet;
WT p_c2b2;
public:
pythagorean_triplet_generator(const result_type& triplet = {3, 4, 5}) :
p_triplet(triplet), p_c2b2(sq(triplet.c) - sq(triplet.b))
{}
const result_type& operator*() const { return p_triplet; }
const result_type* operator->() const { return &p_triplet; }
pythagorean_triplet_generator& operator++() {
do {
if (++p_triplet.b == p_triplet.c) {
++p_triplet.c;
p_triplet.b = ceil(p_triplet.c * M_SQRT1_2);
p_c2b2 = sq(p_triplet.c) - sq(p_triplet.b);
} else
p_c2b2 -= 2 * p_triplet.b - 1;
p_triplet.a = sqrt(p_c2b2);
} while (sq(p_triplet.a) != p_c2b2 || gcd(p_triplet.b, p_triplet.a) != 1);
return *this;
}
result_type operator()() { result_type t = **this; ++*this; return t; }
};
int main(int argc, const char* argv[]) {
const bool verbose = argc > 1;
const int min = 1 << 26;
const int max = sqrt(1ll << 53);
const size_t small_triplet_count = 1000;
vector<pythagorean_triplet<int>> small_triplets;
small_triplets.reserve(small_triplet_count);
generate_n(
back_inserter(small_triplets),
small_triplet_count,
pythagorean_triplet_generator<int>()
);
int found = 0;
auto add = [&] (int x1, int y1, int x2, int y2) {
#ifdef VERIFY
auto n1 = sq(x1) + sq(y1), n2 = sq(x2) + sq(y2);
if (x1 < y1 || x2 < y2 || x1 > max || x2 > max ||
n1 == n2 || sqrt(n1) != sqrt(n2)
) {
fprintf(stderr, "Wrong false-positive: (%d, %d) (%d, %d)\n",
x1, y1, x2, y2);
return;
}
#endif
if (verbose) printf("(%d, %d) (%d, %d)\n", x1, y1, x2, y2);
++found;
};
int output_counter = 0;
for (int x = min; x <= max; ++x) add(x, 0, x, 1);
for (pythagorean_triplet_generator<int> i; i->c <= max; ++i) {
const auto& t1 = *i;
for (int n = div_ceil(min, t1.c); n <= max / t1.c; ++n)
add(n * t1.b, n * t1.a, n * t1.c, 1);
auto find_false_positives = [&] (int r, int x, int y) {
{
int n = div_ceil(min - r, t1.c);
int min_r = r + n * t1.c;
int max_n = n + (max - min_r) / t1.c;
for (; n <= max_n; ++n)
add(r + n * t1.c, 0, x + n * t1.b, y + n * t1.a);
}
for (const auto t2 : small_triplets) {
int m = div_mod_n((t2.c - r % t2.c) % t2.c, t1.c % t2.c, t2.c);
if (m < 0) continue;
int sr = r + m * t1.c;
int c = lcm(t1.c, t2.c);
int min_n = div_ceil(min - sr, c);
int min_r = sr + min_n * c;
if (min_r > max) continue;
int x1 = x + m * t1.b, y1 = y + m * t1.a;
int x2 = t2.b * (sr / t2.c), y2 = t2.a * (sr / t2.c);
int a1 = t1.a * (c / t1.c), b1 = t1.b * (c / t1.c);
int a2 = t2.a * (c / t2.c), b2 = t2.b * (c / t2.c);
int max_n = min_n + (max - min_r) / c;
int max_r = sr + max_n * c;
for (int n = min_n; n <= max_n; ++n) {
add(
x2 + n * b2, y2 + n * a2,
x1 + n * b1, y1 + n * a1
);
}
}
};
{
int m = div_mod_n((t1.a - t1.c % t1.a) % t1.a, t1.b % t1.a, t1.a);
find_false_positives(
/* r = */ (mul(m, t1.c) + t1.b) / t1.a,
/* x = */ (mul(m, t1.b) + t1.c) / t1.a,
/* y = */ m
);
} {
int m = div_mod_n((t1.b - t1.c % t1.b) % t1.b, t1.a, t1.b);
find_false_positives(
/* r = */ (mul(m, t1.c) + t1.a) / t1.b,
/* x = */ m,
/* y = */ (mul(m, t1.a) + t1.c) / t1.b
);
}
if (output_counter++ % 50 == 0)
printf("%d\n", found), fflush(stdout);
}
printf("%d\n", found);
}


As a side comment, it's possible to simultaneously determine whether or not an integer is a perfect square and also compute its precise square root efficiently. The following algorithm is 5x faster than hardware square root on my system (comparing 64-bit unsigned integers to 80-bit long double): http://math.stackexchange.com/questions/41337/efficient-way-to-determine-if-a-number-is-perfect-square/878338#878338
– Todd Lehman – 2014-09-12T19:36:55.063