44
11
There's a 500 rep unofficial bounty for beating the current best answer.
Goal
Your goal is to multiply two numbers using only a very limited set of arithmetic operations and variable assignment.
- Addition
x,y -> x+y - Reciprocal
x -> 1/x(not divisionx,y -> x/y) - Negation
x -> -x(not subtractionx,y -> x-y, though you can do it as two operationsx + (-y)) - The constant
1(no other constants allowed, except as produced by operations from1) - Variable assignment
[variable] = [expression]
Scoring: The values start in variables a and b. Your goal is to save their product a*b into the variable c using as few operations as possible. Each operation and assignment +, -, /, = costs a point (equivalently, each use of (1), (2), (3), or (4)). Constants 1 are free. The fewest-point solution wins. Tiebreak is earliest post.
Allowance: Your expression has to be arithmetically correct for "random" reals a and b. It can fail on a measure-zero subset of R2, i.e. a set that has no area if plotted in the a-b Cartesian plane. (This is likely to be needed due to reciprocals of expressions that might be 0 like 1/a.)
Grammar:
This is an atomic-code-golf. No other operations may be used. In particular, this means no functions, conditionals, loops, or non-numerical data types. Here's a grammar for the allowed operations (possibilities are separated by |). A program is a sequence of <statement>s, where a <statement> is given as following.
<statement>: <variable> = <expr>
<variable>: a | b | c | [string of letters of your choice]
<expr>: <arith_expr> | <variable> | <constant>
<arith_expr>: <addition_expr> | <reciprocal_expr> | <negation_expr>
<addition_expr>: <expr> + <expr>
<reciprocal_expr>: 1/(<expr>)
<negation_expr>: -<expr>
<constant>: 1
You don't actually have to post code in this exact grammar, as long as it's clear what you're doing and your operation count is right. For example, you can write a-b for a+(-b) and count it as two operations, or define macros for brevity.
(There was a previous question Multiply without Multiply, but it allowed a much looser set of operations.)
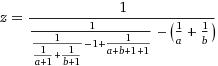
@xnor Currently, I have the answer which works best without assignment allowed (assignment used only once, and will only double it (approximately)). Does that count for the optimal result without assignment, or does it need to be proven to be the optimal result? – proud haskeller – 2015-05-02T17:58:13.477
@proudhaskeller No, I'm looking for a proof of optimality. (Sorry, I had missed your comment in my feed.) – xnor – 2015-05-07T20:30:01.683
4Is this even possible? – Ypnypn – 2014-09-01T20:19:44.460
1@Ypnypn Yes, and I've written an example to make sure. – xnor – 2014-09-01T20:24:15.563
2This feels like a challenge where an optimal solution is likely to be found (once any solution has been found). So what's the tie breaker in that case? – Martin Ender – 2014-09-01T20:27:27.033
1@MartinBüttner Tiebreak is earliest posting in that case. I think there's a good amount of room for optimizations, so I don't think it will just be a race to find one that works and write it cleanly. At least, that's what I found in trying it; maybe someone will find a clearly minimal solution. – xnor – 2014-09-01T20:30:39.550
2Ok since not everyone thought my anwer was as funny as I did, I deleted it and comment here: The rule about the measure zero set is not very wisely chosen since rational numbers are a measure zero set regarding the lebesgue measure, I'd suggest using a certain percentage instead. (Or another kind) But I totally like the idea of this challenge! – flawr – 2014-09-01T21:43:54.903
1@flawr I was imagining the fake language to express arithmetic formulas for real numbers, not act on bits or any sort of finite representation, so I think the measure requirement over the real plane (a,b) ∈ R^2 works fine. But if you actually think it's unclear, I'll edit it. – xnor – 2014-09-01T21:45:41.183
1Of course it is clear what you mean but I think it does not help using precisely defined technical terminology for something that does not meet the definition. Sorry for being a stickler! In my opinion you can also write
I know what you meanor (most as in common sense). – flawr – 2014-09-01T21:47:41.510@flawr I was typing up the same stuff when I saw your comments. Exactly, the set of IEEE floating point numbers is measure zero, and so is all pairs of them. And so is the set of all numbers representable on any machine. – Eric Tressler – 2014-09-01T21:51:08.407
1OK, thanks for the feedback, I guess I should have realize that coders would interpret numbers as stored in bits. I edited it to try to make clear I'm requiring arithmetically correct results for all but a measure-zero set of pairs of real numbers. – xnor – 2014-09-01T21:53:17.723
@xnor How much operations you got when you solved this question? – proud haskeller – 2014-09-04T05:17:33.703
@proudhaskeller 33 :-P It was basically a worse version of algorithmshark's answer. – xnor – 2014-09-04T05:23:17.213
1I don't know that there's a better choice for an algorithmic search other than brute force... And if the actual best solution is, say, 22 operations, that's not really feasible for a brute force search. – rationalis – 2014-09-04T23:57:58.867
I will give a bounty of 300 rep to anyone who posts an optimal solution with proof. A brute force search can be a proof if you explain how it checks everything needed. An optimal result restricted not to use variable assignment will be given 150 rep. Other partial bounties may be given for partial results. – xnor – 2014-10-27T17:45:08.997
@xnor What do you mean by optimal here ? less than 23 operations ? – Optimizer – 2014-10-27T17:50:58.243
@Optimizer No, the best theoretically possible. It might be 23, it might be less. A solution of 22 operations with no proof of optimality would not suffice. (Clarified in the post, thanks.) – xnor – 2014-10-27T17:52:21.707
You mean 22 operations (instead of chars), right ? Also, if someone posts a 24 operations solution, will that count ? – Optimizer – 2014-10-27T17:56:52.140
@Optimizer Yes, operations, thanks. Not sure what you mean about a 24 op solution -- it can't be optimal because there's a 23. If you mean for the no-assignment half-prize, yes, I'd count an optimal solution for that that's more than 23 ops. – xnor – 2014-10-27T17:58:51.777
I see. So the existing 23 operations won't get 300 if no one else posts, right ? Also, are you really sure an answer less than 23 exists ? – Optimizer – 2014-10-27T17:59:53.983