Implement the Game of Life on Anything but a Regular Grid

Question

Conway's Game of Life is (almost) always played on a regular square grid, but it doesn't need to be.

Write a program that implements the standard cell neighboring rules from Conway's Game of Life on a two-dimensional tiling of the Euclidean plane that is not a regular tiling of squares, triangles, or hexagons.

Specifically, the tiling you choose...

1. Must contain at least 2 (but finitely many) differently shaped prototiles.
   • The different shapes may be scaled or rotated versions of each other.
   • They must be able to tile the entire plane without leaving holes.
   • They must be simple polygons with finite perimeter. (They may not be weakly simple.)
2. Must be isomorphically distinct from the square, triangular, and hexagonal grids.
   • Any tiling that trivially boils down to a regular square, triangular, or hexagonal grid is not allowed. (You can still use squares/triangles/hexagons in other tilings.)
   • The border between any two prototiles may contain multiple edges and vertices, but it must be continuous.

Your tiling may be periodic or aperiodic, but when expanded to cover the entire plane, each prototile must appear infinitely many times. (So no "hardcoding" certain parts of your tiling to help achieve the extra points below.)

Each of your prototiles represents one Game of Life cell that neighbors other cells:

• Cells that share any edges or any vertices are considered neighbors.
• Cells that share multiple edges or vertices are still only counted at each others neighbors once.
• Cells cannot neighbor themselves.

Tiling inspiration links:

• http://en.wikipedia.org/wiki/Tiling_by_regular_polygons
• http://en.wikipedia.org/wiki/List_of_uniform_tilings
• http://en.wikipedia.org/wiki/Aperiodic_tiling
• http://en.wikipedia.org/wiki/Penrose_tiling

Output

Your program should output some sort of graphical representation of your tiling with the Game of Life being played in it, which you should of course post in image/gif/jsfiddle format.

Please draw tile edge lines and use a light color for dead cells and a dark color for live cells.

Scoring

Your submission score is the number of upvotes minus downvotes, plus extra points for discovering common Game of Life patterns in your tiling:

• Find a still life - a pattern that doesn't change from one generation to the next. (+2)
• Find oscillators with period 2 through 29. (+3 for every period you find up to a total of 5 periods or +15 points max)
• Find an oscillator with a period of 30 or more. (+7)
• Find a spaceship - something that can get arbitrarily far away from it's starting location without leaving any debris. (It may not necessarily be a moving oscillator.) (+10)
• Find another spaceship that moves in a distinctly different way (and is not a mirrored version of the first spaceship), e.g. see glider and LWSS. (+10)
• Find a pattern of infinite growth. You do not have to prove that the growth is infinite, just show us enough evidence of the pattern that it is practically certain. (+25)
• Find a gun - something that generates spaceships forever (this also counts as infinite growth). (+50)

The infinite growth patterns must start with a finite number of live cells and the other patterns must always contain a bounded number of live cells (e.g. a spaceship should not grow arbitrarily large over time).

Due to the nature of aperiodic tilings it seems likely that many of these patterns would be impossible to implement in them. So any verifiably aperiodic tiling gets +40 points automatically. A pattern that works in one place in an aperiodic tiling does not have to work in other places.

Each of the bonuses can only be applied once. Naturally we'll need to see the output to verify them. The highest score wins.

Notes

• Each answer can only have bonuses applied to one specific tiling. (Though feel free to include related tilings.)
• The Game of Life rules are as follows:
  1. Any live cell with less than 2 or more than 3 live neighbors dies.
  2. Any dead cell with exactly 3 live neighbors comes alive.
  3. Other cells do not change.
• Patterns for the extra points should be possible regardless of boundary conditions, but otherwise you may choose any boundary conditions you want.
• By default the background should be all dead tiles.

Thanks to Peter Taylor, Jan Dvorak, and githubphagocyte for helping to hammering out loopholes in what tilings should be allowed.

^{(In case anyone is curious, this is definitely my favorite of my own challenges.)}

Answer 1

Penrose rhombii in Python, +97 points

I chose a penrose tiling composed of two different shaped rhombuses, meeting 3-8 per vertex. This penrose tiling is proven aperiodic elsewhere. The simulation is graphical (via pygame) and interactive. Comments indicate two places in the code where algorithm implementation was taken from another source.

There are many small neighborhood still lifes:

Any vertex with four "on" neighbors is a still life:

Any loop where no dead interior cells touch three cells on the loop is also a still life:

There are oscillators at various frequencies:

p2: (many variations)

p3:

p4:

p5:

p6:

p7:

p12:

p20:

The rules and clarifications as written mostly do not allow for gliders or guns in a non-planned aperiodic tiling. That leaves infinite growth, which I would argue isn't likely, and a p30+ oscillator, which almost certainly exists but will take a while to find.

python penrose-life.py will generate a single randomly colored periodic tiling python -O penrose-life.py or just ./penrose-life.py will actually run the simulation. While running it will try to identify oscillators, and when it finds one (p>2) it will screenshot it. After recording an oscillator, or a stalled board, the board is randomized.

Clicking a cell in the simulation will toggle it.

The following keyboard shortcuts exist in the simulation:

• Escape - quit the program
• Space - randomize the whole board
• P - pause the simulation
• S - single step the simulation
• F - toggle "fast" mode, rendering only every 25th frame

The initial seed of the penrose tiling algorithm is a circle of ten narrow triangles. This could be changed to single triangle, or a different arrangement of triangles, symmetric or not.

Source:

#!/usr/bin/env python -O

# tiling generation code originally from http://preshing.com/files/penrose.py

import sys
import math
import time
import cairo
import cmath
import random
import pygame

#TODO: command line parameters
#------ Configuration --------
IMAGE_SIZE = (1200, 1200)
OFFX = 600
OFFY = 600
RADIUS = 600
if __debug__: NUM_SUBDIVISIONS = 5
else: NUM_SUBDIVISIONS = 7
#-----------------------------

goldenRatio = (1 + math.sqrt(5)) / 2

class Triangle():
    def __init__(self, parent = None, color = 0, corners = []):
        self.parent = parent
        self.other_half = None
        # immediate neighbor 0 is on BA side, 1 is on AC side
        self.neighbors = [None, None]
        # all_neighbors includes diagonal neighbors
        self.all_neighbors = set()
        # child 0 is first on BA side, 1 is second, 2 is on AC side
        self.children = []
        self.color = color
        if __debug__: self.debug_color = (random.random(),random.random(),random.random())
        self.state = random.randint(0,1)
        self.new_state = 0
        self.corners = corners
        self.quad = None
    def __repr__(self):
        return "Triangle: state=" + str(self.state) + \
            " color=" + str(self.color) + \
            " parent=" + ("yes" if self.parent else "no") + \
            " corners=" + str(self.corners)
    # break one triangle up into 2-3 smaller triangles
    def subdivide(self):
        result = []
        A,B,C = self.corners
        if self.color == 0:
            # Subdivide red triangle
            P = A + (B - A) / goldenRatio
            result = [Triangle(self, 0, (C, P, B)), Triangle(self, 1, (P, C, A))]
        else:
            # Subdivide blue triangle
            Q = B + (A - B) / goldenRatio
            R = B + (C - B) / goldenRatio
            result = [Triangle(self, 1, (Q, R, B)), Triangle(self, 0, (R, Q, A)), Triangle(self, 1, (R, C, A))]
        self.children.extend(result)
        return result;
    # identify the left and right neighbors of a triangle
    def connect_immediate(self):
        o = None
        n = self.neighbors
        if self.parent:
            if self.color == 0: # red child
                if self.parent.color == 0: # red parent
                    if self.parent.neighbors[0]:
                        if self.parent.neighbors[0].color == 0: # red left neighbor
                            o = self.parent.neighbors[0].children[0]
                        else: # blue left neighbor
                            o = self.parent.neighbors[0].children[1]
                    n[0] = self.parent.children[1]
                    if self.parent.other_half:
                        n[1] = self.parent.other_half.children[0]
                else: # blue parent
                    if self.parent.neighbors[0]:
                        if self.parent.neighbors[0].color == 0: # red left neighbor
                            o = self.parent.neighbors[0].children[0]
                        else: # blue left neighbor
                            o = self.parent.neighbors[0].children[1]
                    n[0] = self.parent.children[0]
                    n[1] = self.parent.children[2]
            else: # blue child
                if self.parent.color == 0: # red parent
                    if self.parent.neighbors[1]:
                        if self.parent.neighbors[1].color == 0: # red right neighbor
                            o = self.parent.neighbors[1].children[1]
                        else: # blue right neighbor
                            o = self.parent.neighbors[1].children[2]
                    n[0] = self.parent.children[0]
                    if self.parent.neighbors[0]:
                        if self.parent.neighbors[0].color == 0: # red left neighbor
                            n[1] = self.parent.neighbors[0].children[1]
                        else: # blue left neighbor
                            n[1] = self.parent.neighbors[0].children[0]
                else: # blue child of blue parent
                    if self.corners[2] == self.parent.corners[1]: # first blue child
                        if self.parent.other_half:
                            o = self.parent.other_half.children[0]
                        n[0] = self.parent.children[1]
                        if self.parent.neighbors[0]:
                            if self.parent.neighbors[0].color == 0: # red left neighbor
                                n[1] = self.parent.neighbors[0].children[1]
                            else: #blue left neighbor
                                n[1] = self.parent.neighbors[0].children[0]
                    else: # second blue child
                        if self.parent.neighbors[1]:
                            if self.parent.neighbors[1].color == 0: # red right neighbor
                                o = self.parent.neighbors[1].children[1]
                            else: # blue right neighbor
                                o = self.parent.neighbors[1].children[2]
                        if self.parent.other_half:
                            n[0] = self.parent.other_half.children[2]
                        n[1] = self.parent.children[1]
        self.other_half = o
        if o:
            self.state = self.other_half.state
            if __debug__: self.debug_color = self.other_half.debug_color

#TODO: different seed triangle configurations
# Create wheel of red triangles around the origin
triangles = [[]]
for i in xrange(10):
    B = cmath.rect(RADIUS, (2*i - 1) * math.pi / 10)+OFFX+OFFY*1j
    C = cmath.rect(RADIUS, (2*i + 1) * math.pi / 10)+OFFX+OFFY*1j
    if i % 2 == 0:
        B, C = C, B  # Make sure to mirror every second triangle
    triangles[0].append(Triangle(None, 0, (OFFX+OFFY*1j, B, C)))

# identify the neighbors of the starting triangles
for i in xrange(10):
    if i%2:
        triangles[0][i].neighbors[0] = triangles[0][(i+9)%10]
        triangles[0][i].neighbors[1] = triangles[0][(i+1)%10]
    else:
        triangles[0][i].neighbors[1] = triangles[0][(i+9)%10]
        triangles[0][i].neighbors[0] = triangles[0][(i+1)%10]

# Perform subdivisions
for i in xrange(NUM_SUBDIVISIONS):
    triangles.append([])
    for t in triangles[i]:
        triangles[i+1].extend(t.subdivide())
    for t in triangles[i+1]:
        t.connect_immediate()

# from here on, we only deal with the most-subdivided triangles
tris = triangles[NUM_SUBDIVISIONS]

# make a dict of every vertex, containing a list of every triangle sharing that vertex
vertices = {}
for t in tris:
    for c in t.corners:
        if c not in vertices:
            vertices[c] = []
        vertices[c].append(t)

# every triangle sharing a vertex are neighbors of each other
for v,triset in vertices.iteritems():
    for t in triset:
        t.all_neighbors.update(triset)

# combine mirrored triangles into quadrilateral cells
quads = []
total_neighbors = 0
for t in tris:
    if t.quad == None and t.other_half != None:
        quads.append(t)
        q = t
        q.corners = (q.corners[0], q.corners[1], q.other_half.corners[0], q.corners[2])
        q.quad = q
        q.other_half.quad = q
        q.all_neighbors.update(q.other_half.all_neighbors)
        q.all_neighbors.remove(q.other_half)
        q.all_neighbors.remove(q)
        total_neighbors += len(q.all_neighbors)

# clean up quads who still think they have triangles for neighbors
for q in quads:
    new_neighbors = set()
    for n in q.all_neighbors:
        if len(n.corners)==3:
            if n.other_half:
                if len(n.other_half.corners)==4:
                    new_neighbors.add(n.other_half)
        else:
            new_neighbors.add(n)
    q.all_neighbors = new_neighbors


# # adopt your other half's neighbors, minus them and yourself. mark other half as dead.
# for t in tris:
#     if t.other_half:
#         t.all_neighbors.update(t.other_half.all_neighbors)
#     t.all_neighbors.remove(t)
#     if t.other_half and t.other_half in t.all_neighbors:
#         t.all_neighbors.remove(t.other_half)
#     if t.other_half and not t.dead_half:
#         t.other_half.dead_half = True

pygame.init()
screen = pygame.display.set_mode(IMAGE_SIZE, 0, 32)
pygame.display.set_caption("Penrose Life")
pygame.display.flip()

paused = False
fast = False
randomize = True
found_oscillator = 0
randomized_tick = 0
tick = 0
timed_tick = 0
timed_tick_time = time.clock()
render_countdown = 0

history_length = 45
quad_history = [[0]*len(quads)]*history_length
quad_pointer = 0

myfont = pygame.font.SysFont("monospace", 15)
guidish = random.randint(0,99999999)

while True:

    tick += 1
    if tick - randomized_tick > 1000 and render_countdown == 0:
        randomize = True
    edited = False
    step = False
    if found_oscillator > 0 and render_countdown == 0:
        print "Potential p" + str(found_oscillator) + " osillator"
        render_countdown = found_oscillator
    if render_countdown == 0: # don't handle input while rendering an oscillator
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                sys.exit(0)
            elif event.type == pygame.KEYDOWN:
                # print event
                if event.scancode == 53: # escape
                    sys.exit(0)
                elif event.unicode == " ": # randomize
                    randomize = True
                    edited = True
                elif event.unicode == "p": # pause
                    paused = not paused
                elif event.unicode == "f": # fast
                    fast = not fast
                elif event.unicode == "s": # step
                    paused = True
                    step = True
            elif event.type == pygame.MOUSEBUTTONDOWN:
            # click to toggle a cell
                x = event.pos[0]
                y = event.pos[1]
                for q in quads:
                    poly = [(c.real,c.imag) for c in q.corners]
                    # http://www.ariel.com.au/a/python-point-int-poly.html
                    n = len(poly)
                    inside = False
                    p1x,p1y = poly[0]
                    for i in range(n+1):
                        p2x,p2y = poly[i % n]
                        if y > min(p1y,p2y):
                            if y <= max(p1y,p2y):
                                if x <= max(p1x,p2x):
                                    if p1y != p2y:
                                        xinters = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                                    if p1x == p2x or x <= xinters:
                                        inside = not inside
                        p1x,p1y = p2x,p2y
                    if inside:
                        edited = True
                        q.state = 0 if q.state==1 else 1

    if randomize and render_countdown == 0:
        randomized_tick = tick
        randomize = False
        for q in quads:
            q.state = random.randint(0,1)
            edited = True

    if (not fast) or (tick%25==0) or edited or render_countdown > 0:
        # draw filled quads
        for q in quads:
            cs = [(c.real,c.imag) for c in q.corners]
            if __debug__:
                color = q.debug_color
                color = (int(color[0]*256)<<24)+(int(color[1]*256)<<16)+(int(color[2]*256)<<8)+0xFF
            else:
                if q.state == 0:
                    color = 0xFFFFFFFF
                else:
                    color = 0x000000FF
            pygame.draw.polygon(screen, color, cs, 0)
        # draw edges
        for q in quads:
            if len(q.corners)==3:
                exit(1)
            cs = [(c.real,c.imag) for c in q.corners]
            width = 3
            pygame.draw.lines(screen, 0x7F7F7FFF, 1, cs, int(width))
        now = time.clock()
        speed = (tick-timed_tick)/(now-timed_tick_time)
        timed_tick_time = now
        timed_tick = tick
        screen.blit(screen, (0, 0))
        label = myfont.render("%4.2f/s"%speed, 1, (255,255,255))
        screen.fill(pygame.Color("black"), (0, 0, 110, 15))
        screen.blit(label, (0, 0))        
        pygame.display.update()

    if __debug__:
        break

    if paused and not step and render_countdown == 0:
        time.sleep(0.05)
        continue

    # screenshot
    if render_countdown > 0:
        filename = "oscillator_p%03d_%08d_%03d.png" % (found_oscillator, guidish, found_oscillator - render_countdown)
        pygame.image.save(screen,filename)
        render_countdown -= 1
        if render_countdown == 0:
            guidish = random.randint(0,99999999)
            found_oscillator = 0
            randomize = True
            continue


    # calculate new cell states based on the Game of Life rules
    for q in quads:
        a = sum([n.state for n in q.all_neighbors])
        q.new_state = q.state
        # dead cells with three neighbors spawn
        if q.state == 0 and a == 3:
            q.new_state = 1
        # live cells only survive with two or three neighbors
        elif a < 2 or a > 3:
            q.new_state = 0

    # update cell states
    for q in quads:
        q.state = q.new_state

    this_state = [q.state for q in quads]

    # don't bother checking
    if render_countdown == 0:
        # compare this board state to the last N-1 states
        for i in range(1,history_length):
            if quad_history[(quad_pointer-i)%history_length] == this_state:
                if i == 1 or i == 2: # stalled board or p2 oscillator (boring)
                    randomize = True
                    break
                #TODO: give up if the "oscillator" includes border cells
                #TODO: identify cases of two oprime oscillators overlapping
                elif i > 2:
                    found_oscillator = i
                    break # don't keep looking

        # remember this board state
        quad_history[quad_pointer] = this_state
        quad_pointer = (quad_pointer+1)%history_length

if __debug__:
    filename = "penrose.png"
    pygame.image.save(screen,filename)
    time.sleep(1)

Answer 2

C++ w/ OpenGL (+17)

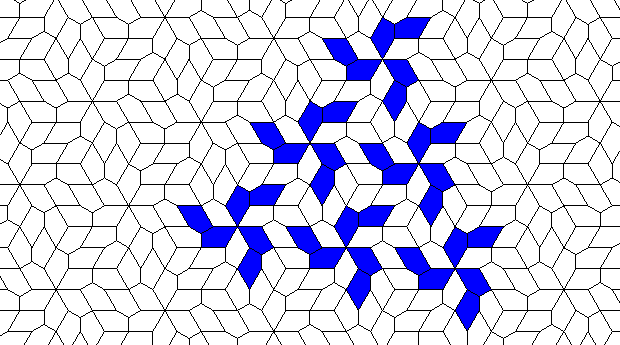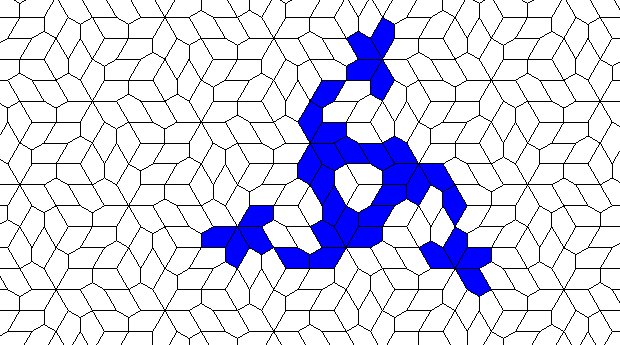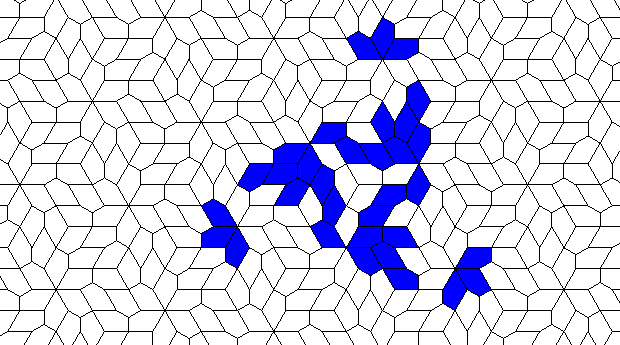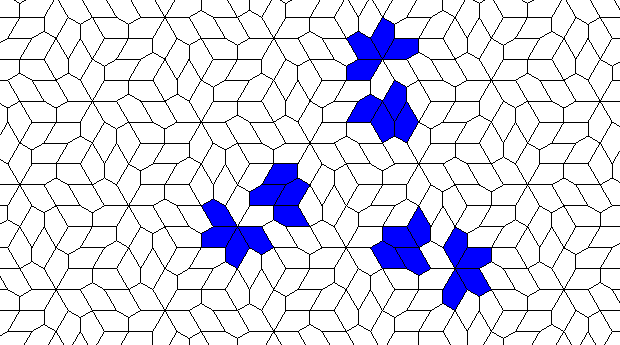
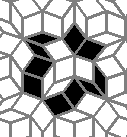
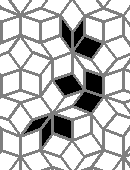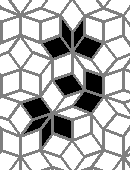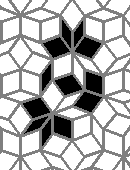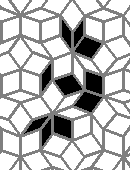
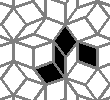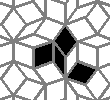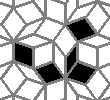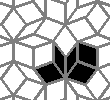
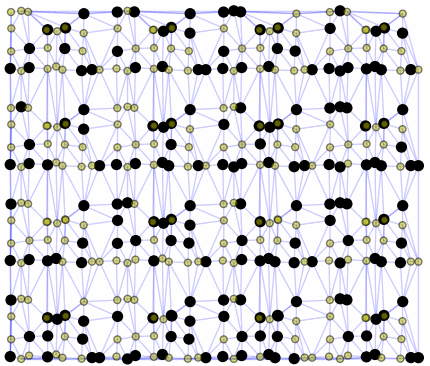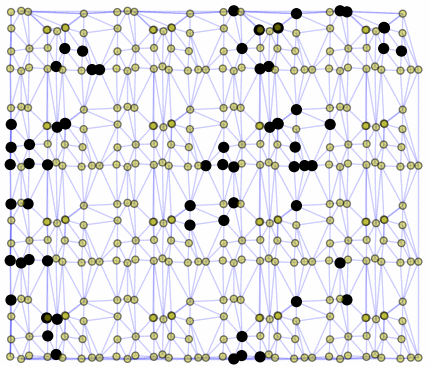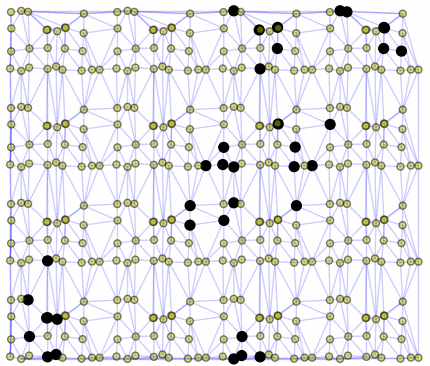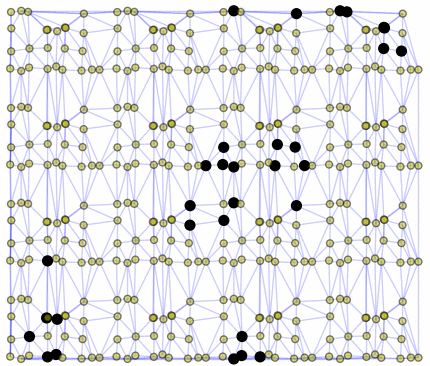
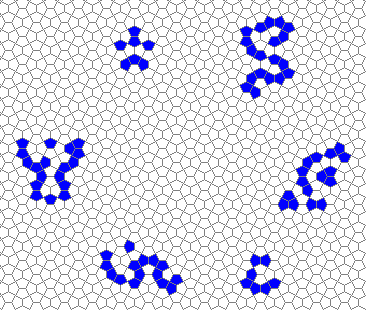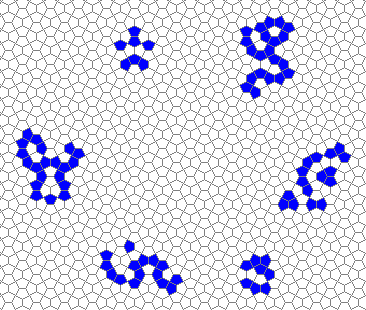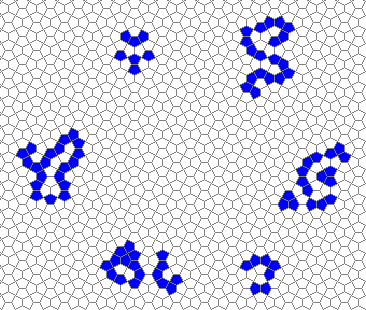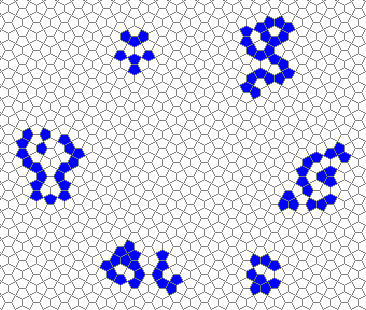
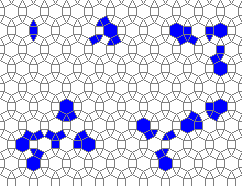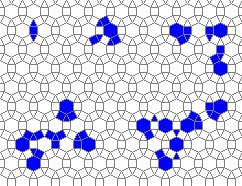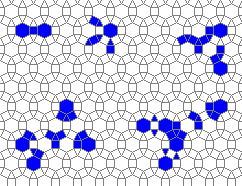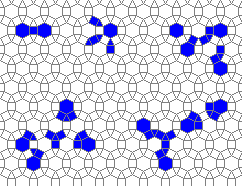
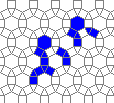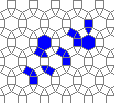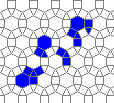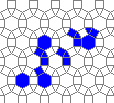
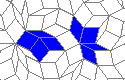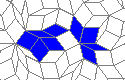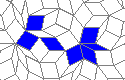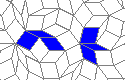
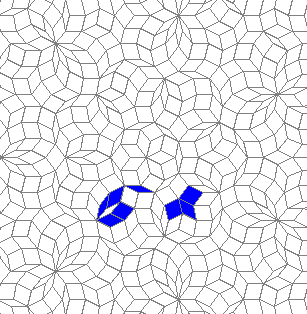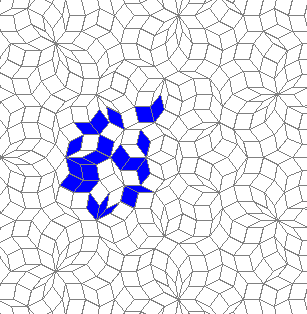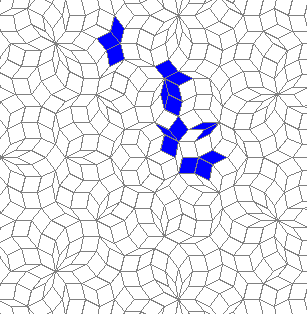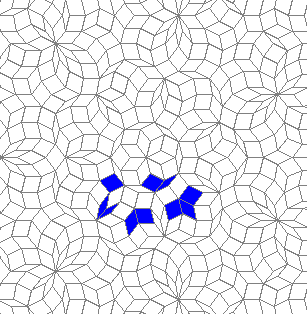
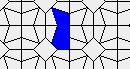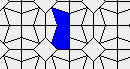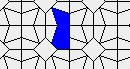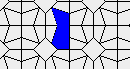
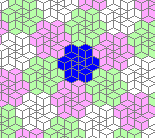
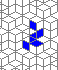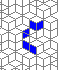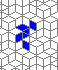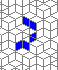
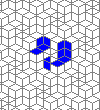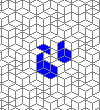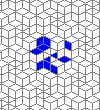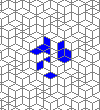
So I tried 3-Isohedral convex pentagon grid. Works for me ;) Standard game of life rules apply, except the grid is not infinite - there are border cells outside the image. 30% of the cells are initially alive.

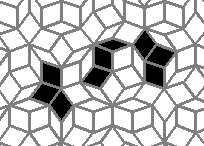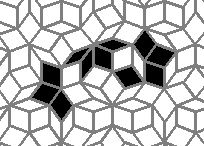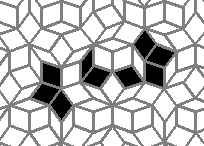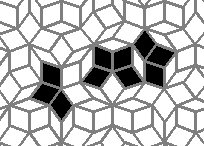
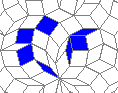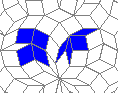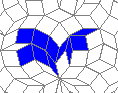
This is how the grid looks like:

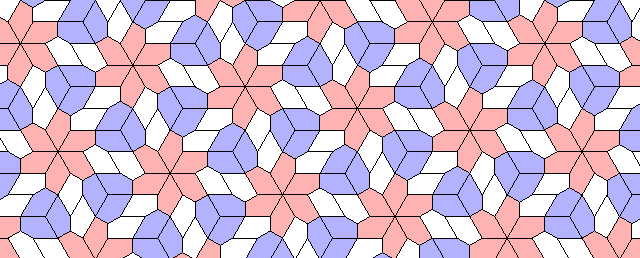
The live version:

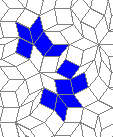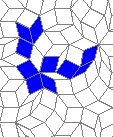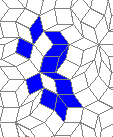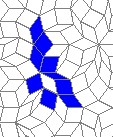
Blue cells are alive, white are dead. Red cells just died, green were just born. Note that the artifacts in the image are the result of gif compression, SO doesn't like 10MB gifs :(.

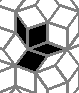
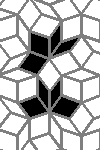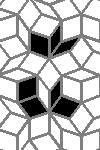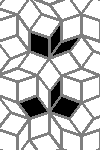
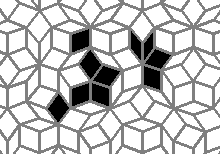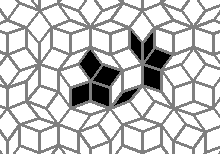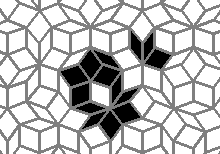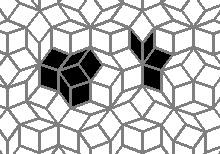
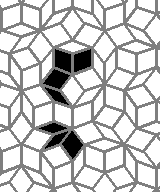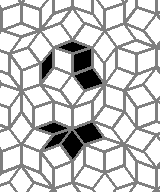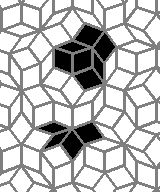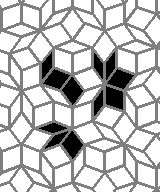
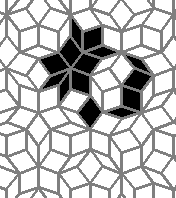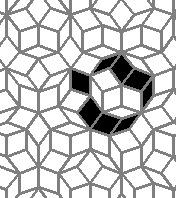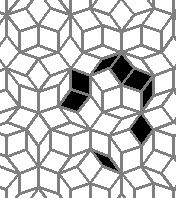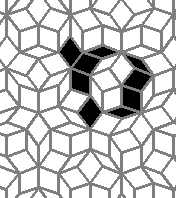
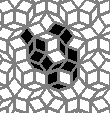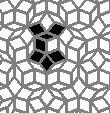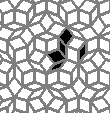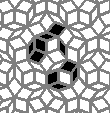
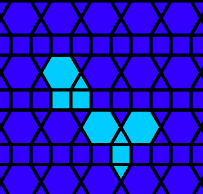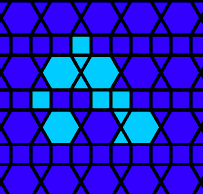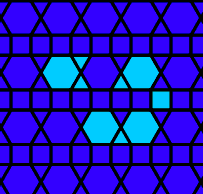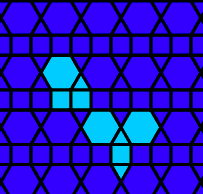
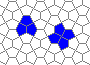
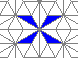
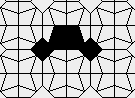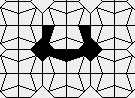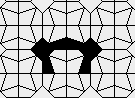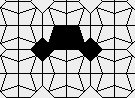
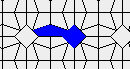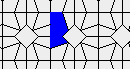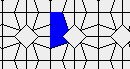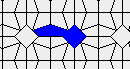
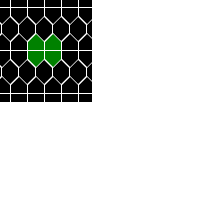
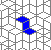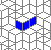
Still life: (+2)

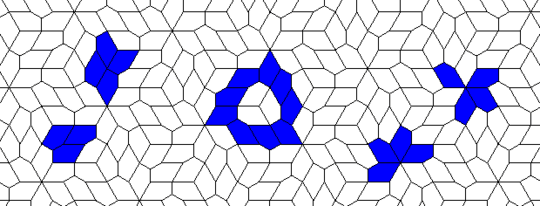
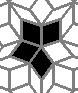
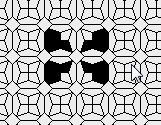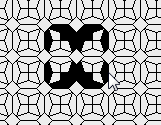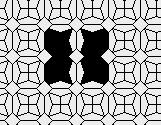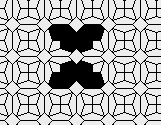
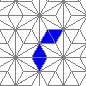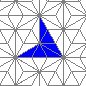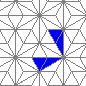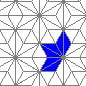
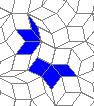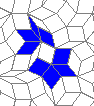
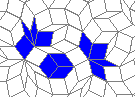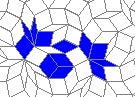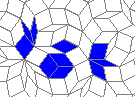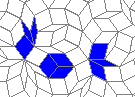
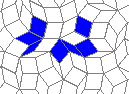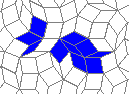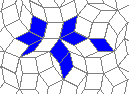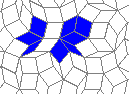
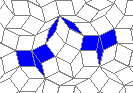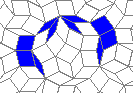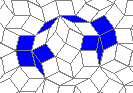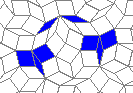
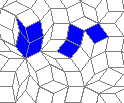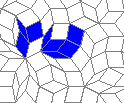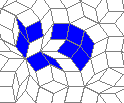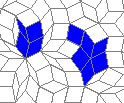
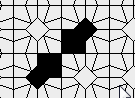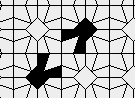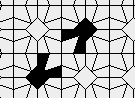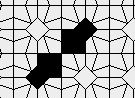
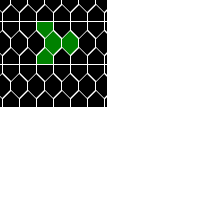
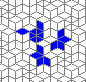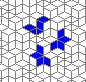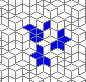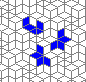
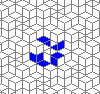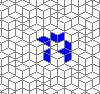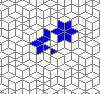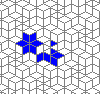
Oscillators T=2, T=3, T=12: (+9)

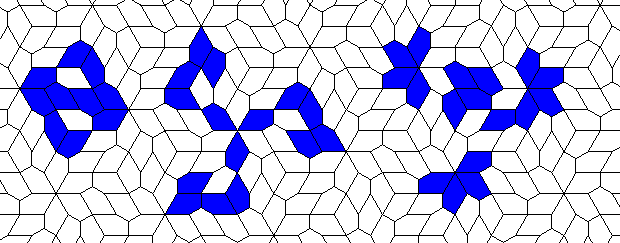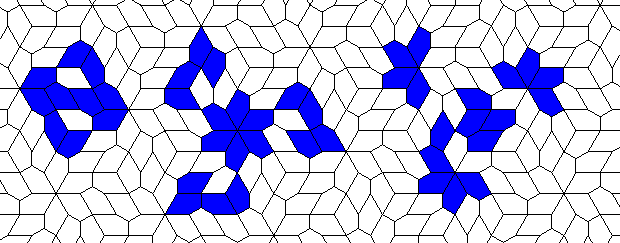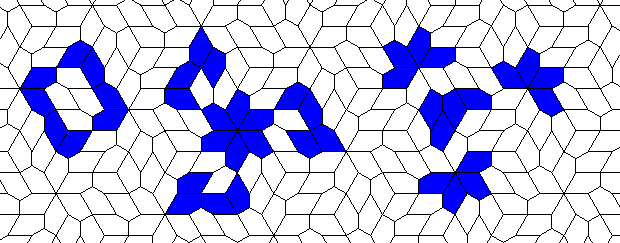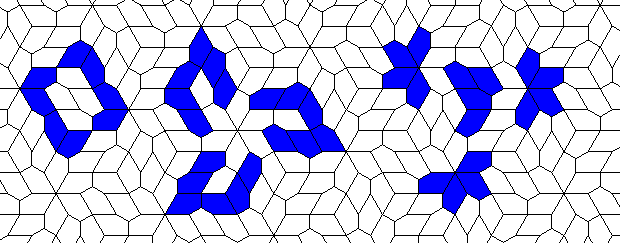
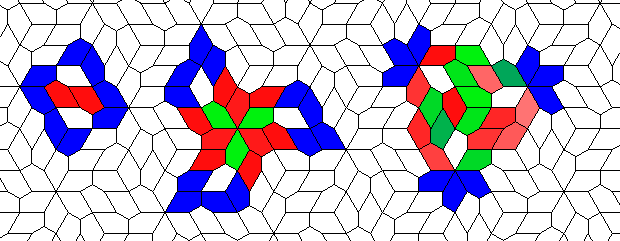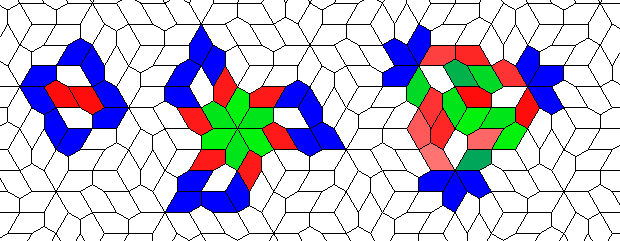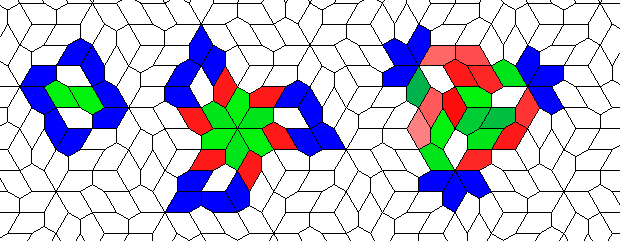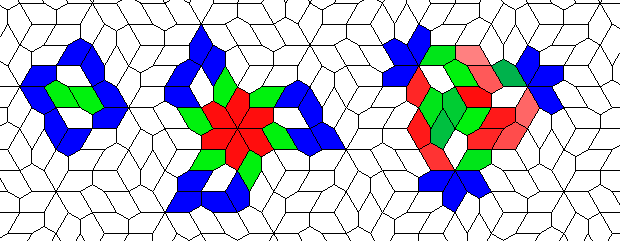
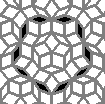
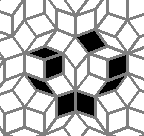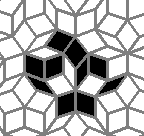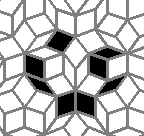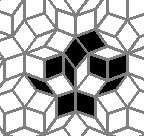
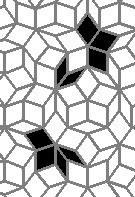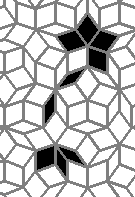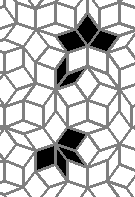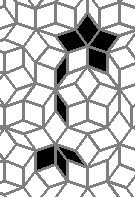
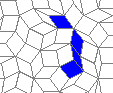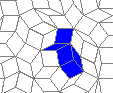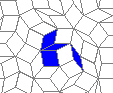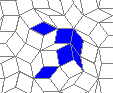
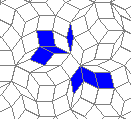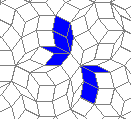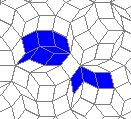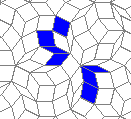
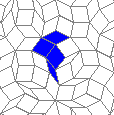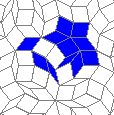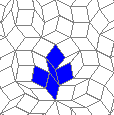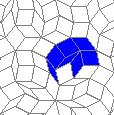
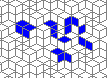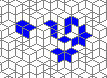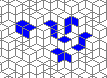
Oscillators T=6 , T=7: (+6)

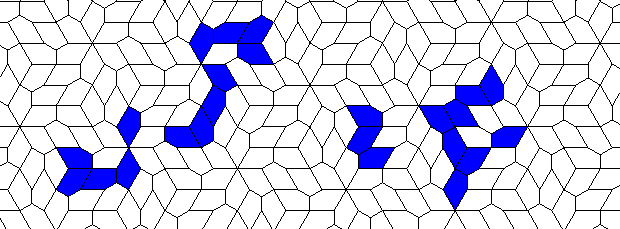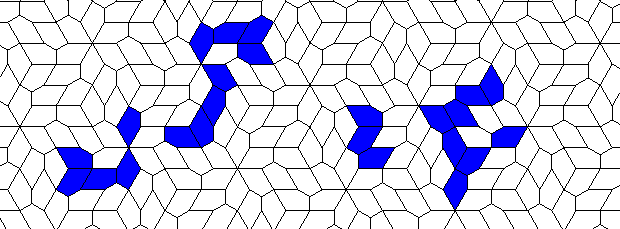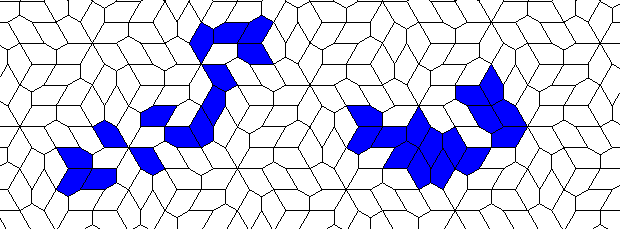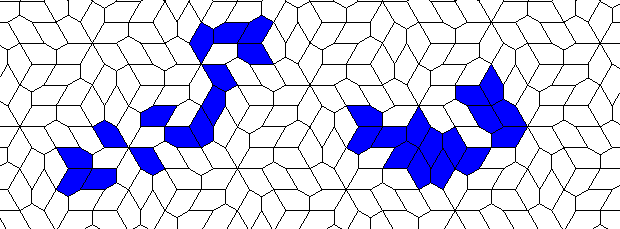
There are many more different oscillators... But it seems that the grid is not regular enough for a ship...

This is nothing (no points), but I like it:

The code is a mess :) Uses some ancient fixed OpenGL. Otherwise used GLEW, GLFW, GLM and ImageMagick for gif export.

/**
 * Tile pattern generation is inspired by the code 
 * on http://www.jaapsch.net/tilings/
 * It saved me a lot of thinkink (and debugging) - thank you, sir!
 */

#include <GL/glew.h>
#include <GLFW/glfw3.h>
#include <FTGL/ftgl.h>  //debug only
#include <ImageMagick-6/Magick++.h> //gif export
#include "glm/glm.hpp" 

#include <iostream>
#include <array>
#include <vector>
#include <set>
#include <algorithm>
#include <unistd.h>

typedef glm::vec2 Point;
typedef glm::vec3 Color;

struct Tile {
    enum State {ALIVE=0, DEAD, BORN, DIED, SIZE};

    static const int VERTICES = 5;
    static constexpr float SCALE = 0.13f;
    static constexpr std::array<std::array<int, 7>, 18> DESC 
    {{
        {{1, 0,0, 0,0,0, 0}},
        {{0, 1,2, 0,2,1, 0}},
        {{2, 2,3, 0,2,3, 1}},
        {{1, 0,4, 0,0,1, 0}},
        {{0, 1,2, 3,2,1, 0}},
        {{2, 2,3, 3,2,3, 1}},
        {{1, 0,4, 3,0,1, 0}},
        {{0, 1,2, 6,2,1, 0}},
        {{2, 2,3, 6,2,3, 1}},
        {{1, 0,4, 6,0,1, 0}},
        {{0, 1,2, 9,2,1, 0}},
        {{2, 2,3, 9,2,3, 1}},
        {{1, 0,4, 9,0,1, 0}},
        {{0, 1,2,12,2,1, 0}},
        {{2, 2,3,12,2,3, 1}},
        {{1, 0,4,12,0,1, 0}},
        {{0, 1,2,15,2,1, 0}},
        {{2, 2,3,15,2,3, 1}}
    }};

    const int ID;
    std::vector<Point> coords;
    std::set<Tile*> neighbours;
    State state;
    State nextState;
    Color color;

    Tile() : ID(-1), state(DEAD), nextState(DEAD), color(1, 1, 1) {
        const float ln = 0.6f;
        const float h = ln * sqrt(3) / 2.f;
        coords = {
            Point(0.f,      0.f), 
            Point(ln,       0.f), 
            Point(ln*3/2.f,h), 
            Point(ln,       h*4/3.f), 
            Point(ln/2.f,   h)
        };
        for(auto &c : coords) {
            c *= SCALE;
        }
    }

    Tile(const int id, const std::vector<Point> coords_) : 
        ID(id), coords(coords_), state(DEAD), nextState(DEAD), color(1, 1, 1) {}

    bool operator== (const Tile &other) const {
        return ID == other.ID;
    }

    const Point & operator[] (const int i) const {
        return coords[i];
    }
    void updateState() {
        state = nextState;
    }
    /// returns "old" state
    bool isDead() const {
        return state == DEAD || state == DIED;
    }
    /// returns "old" state
    bool isAlive() const {
        return state == ALIVE || state == BORN;
    }

    void translate(const Point &p) {
       for(auto &c : coords) {
           c += p;
       }
    }

    void rotate(const Point &p, const float angle) {
        const float si = sin(angle);
        const float co = cos(angle);
        for(auto &c : coords) {
            Point tmp = c - p;
            c.x = tmp.x * co - tmp.y * si + p.x;
            c.y = tmp.y * co + tmp.x * si + p.y;
        }      
    }

    void mirror(const float y2) {
       for(auto &c : coords) {
          c.y = y2 - (c.y - y2);
       }
    }

};
std::array<std::array<int, 7>, 18> constexpr Tile::DESC;
constexpr float Tile::SCALE;

class Game {
    static const int    CHANCE_TO_LIVE  = 30;       //% of cells initially alive
    static const int    dim             = 4;        //evil grid param

    FTGLPixmapFont &font;
    std::vector<Tile> tiles;
    bool animate; //animate death/birth
    bool debug; //show cell numbers (very slow)
    bool exportGif;     //save gif
    bool run;

public: 
    Game(FTGLPixmapFont& font) : font(font), animate(false), debug(false), exportGif(false), run(false) {
        //create the initial pattern
        std::vector<Tile> init(18);
        for(int i = 0; i < Tile::DESC.size(); ++i) {
            auto &desc = Tile::DESC[i];
            Tile &tile = init[i];
            switch(desc[0]) {   //just to check the grid
                case 0: tile.color = Color(1, 1, 1);break;
                case 1: tile.color = Color(1, 0.7, 0.7);break;
                case 2: tile.color = Color(0.7, 0.7, 1);break;
            }

            if(desc[3] != i) {
                const Tile &tile2 = init[desc[3]];
                tile.translate(tile2[desc[4]] - tile[desc[1]]);
                if(desc[6] != 0) {
                   float angleRad = getAngle(tile[desc[1]], tile[desc[2]]);
                   tile.rotate(tile[desc[1]], -angleRad);
                   tile.mirror(tile[desc[1]].y);
                   angleRad = getAngle(tile[desc[1]], tile2[desc[5]]);
                   tile.rotate(tile[desc[1]], angleRad);
                }
                else {
                   float angleRad = getAngle(tile[desc[1]], tile[desc[2]], tile2[desc[5]]);
                   tile.rotate(tile[desc[1]], angleRad);
                }
            }
        }

        const float offsets[4] {
            init[2][8].x - init[8][9].x,
            init[2][10].y - init[8][11].y,
            init[8][12].x - init[14][13].x,
            init[8][14].y - init[14][15].y 
        };

        // create all the tiles
        for(int dx = -dim; dx <= dim; ++dx) { //fuck bounding box, let's hardcode it
            for(int dy = -dim; dy <= dim; ++dy) {

                for(auto &tile : init) {
                    std::vector<Point> vert;
                    for(auto &p : tile.coords) {
                        float ax = dx * offsets[0] + dy * offsets[2];
                        float ay = dx * offsets[1] + dy * offsets[3];
                        vert.push_back(Point(p.x + ax, p.y + ay));
                    }
                    tiles.push_back(Tile(tiles.size(), vert));
                    tiles.back().color = tile.color;
                    tiles.back().state = tile.state;
                }
            }
        }

        //stupid bruteforce solution, but who's got time to think..
        for(Tile &tile : tiles) { //find neighbours for each cell 
            for(Tile &t : tiles) {
                if(tile == t) continue;
                for(Point &p : t.coords) {
                    for(Point &pt : tile.coords) {
                        if(glm::distance(p, pt) < 0.01 ) {
                            tile.neighbours.insert(&t);
                            break;
                        }
                    }
                }
            }
            assert(tile.neighbours.size() <= 9);
        }   
    }

    void init() {
        for(auto &t : tiles) {
            if(rand() % 100 < CHANCE_TO_LIVE) {
                t.state = Tile::BORN;
            }
            else {
                t.state = Tile::DEAD;           
            }
        }
    }

    void update() {
        for(auto &tile: tiles) {
            //check colors
            switch(tile.state) {
                case Tile::BORN:    //animate birth
                    tile.color.g -= 0.05;
                    tile.color.b += 0.05;
                    if(tile.color.b > 0.9) {
                        tile.state = Tile::ALIVE;
                    }
                    break;
                case Tile::DIED:    //animate death
                    tile.color += 0.05;
                    if(tile.color.g > 0.9) {
                        tile.state = Tile::DEAD;
                    }
                    break;
            }
            //fix colors after animation
            switch(tile.state) {
                case Tile::ALIVE:
                    tile.color = Color(0, 0, 1);
                    break;
                case Tile::DEAD:
                    tile.color = Color(1, 1, 1);
                    break;
            }

            //draw polygons
            glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
            glBegin(GL_POLYGON);
            glColor3f(tile.color.r, tile.color.g, tile.color.b);
            for(auto &pt : tile.coords) {
                glVertex2f(pt.x, pt.y); //haha so oldschool!
            }
            glEnd();
        }

        //draw grid
        glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
        glColor3f(0, 0, 0);
        for(auto &tile : tiles) {
            glBegin(GL_POLYGON);
            Point c;    //centroid of tile
            for(auto &pt : tile.coords) {
                glVertex2f(pt.x, pt.y);
                c += pt;
            }
            glEnd();
            if(debug) {
                c /= (float) Tile::VERTICES;
                glRasterPos2f(c.x - 0.025, c.y - 0.01);
                font.Render(std::to_string(tile.ID).c_str()); // 
            }
        }

        if(!run) {
            return;
        }

        //compute new generation
        for(Tile &tile: tiles) {

            tile.nextState = tile.state; //initialize next state
            int c = 0;
            for(auto *n : tile.neighbours) {
                if(n->isAlive()) c++;
            }
            switch(c) {
                case 2:
                    break;
                case 3:
                    if(tile.isDead()) {
                        tile.nextState = animate ? Tile::BORN : Tile::ALIVE;
                        tile.color = Color(0, 1, 0);
                    }
                    break;
                default:
                    if(tile.isAlive()) {
                        tile.nextState = animate ? Tile::DIED : Tile::DEAD;
                        tile.color = Color(1, 0, 0);
                    }
                    break;
            }
        }
        //switch state to new
        for(Tile &tile: tiles) {
            tile.updateState();
        }
    }

    void stop() {run = false;}
    void switchRun() {run = !run;}
    bool isRun() {return run;}
    void switchAnim() {animate = !animate;}
    bool isAnim() {return animate;}
    void switchExportGif() {exportGif = !exportGif;}
    bool isExportGif() {return exportGif;}
    void switchDebug() {debug = !debug;}
    bool isDebug() const {return debug;}
 private:
    static float getAngle(const Point &p0, const Point &p1, Point const &p2) {
       return atan2(p2.y - p0.y, p2.x - p0.x) - atan2(p1.y - p0.y, p1.x - p0.x);
    }

    static float getAngle(const Point &p0, const Point &p1) {
       return atan2(p1.y - p0.y, p1.x - p0.x);
    }
};

class Controlls {
    Game *game;
    std::vector<Magick::Image> *gif;
    Controlls() : game(nullptr), gif(nullptr) {}
public:
    static Controlls& getInstance() {
        static Controlls instance;
        return instance;
    }

    static void keyboardAction(GLFWwindow* window, int key, int scancode, int action, int mods) {
        getInstance().keyboardActionImpl(key, action);
    }

    void setGame(Game *game) {
        this->game = game;
    }
    void setGif(std::vector<Magick::Image> *gif) {
        this->gif = gif;
    }
private:    
    void keyboardActionImpl(int key, int action) {
        if(!game || action == GLFW_RELEASE) {
            return;
        }
        switch (key) {
            case 'R':
                game->stop();
                game->init();
                if(gif) gif->clear();
                break;
            case GLFW_KEY_SPACE:
                game->switchRun();
                break;
            case 'A':
                game->switchAnim();
                break;
            case 'D':
                game->switchDebug();
                break;
                break;
            case 'G':
                game->switchExportGif();
                break;
        };
    }
};

int main(int argc, char** argv) {
    const int width         = 620;      //window size
    const int height        = 620;
    const std::string window_title  ("Game of life!");
    const std::string font_file     ("/usr/share/fonts/truetype/arial.ttf");
    const std::string gif_file      ("./gol.gif");

    if(!glfwInit()) return 1;

    GLFWwindow* window = glfwCreateWindow(width, height, window_title.c_str(), NULL, NULL);
    glfwSetWindowPos(window, 100, 100);
    glfwMakeContextCurrent(window);

    GLuint err = glewInit();
    if (err != GLEW_OK) return 2;

    FTGLPixmapFont font(font_file.c_str());
    if(font.Error()) return 3;
    font.FaceSize(8);

    std::vector<Magick::Image> gif; //gif export
    std::vector<GLfloat> pixels(3 * width * height);

    Game gol(font);
    gol.init();
    Controlls &controlls = Controlls::getInstance();
    controlls.setGame(&gol);
    controlls.setGif(&gif);

    glfwSetKeyCallback(window, Controlls::keyboardAction);

    glClearColor(1.f, 1.f, 1.f, 0);
    while(!glfwWindowShouldClose(window) && !glfwGetKey(window, GLFW_KEY_ESCAPE)) {
        glClear(GL_COLOR_BUFFER_BIT);

        gol.update();

        //add layer to gif
        if(gol.isExportGif()) {
            glReadPixels(0, 0, width, height, GL_RGB, GL_FLOAT, &pixels[0]);
            Magick::Image image(width, height, "RGB", Magick::FloatPixel, &pixels[0]);
            image.animationDelay(50);
            gif.push_back(image);
        }

        std::string info = "ANIMATE (A): ";
        info += gol.isAnim() ? "ON " : "OFF";
        info += " | DEBUG (D): ";
        info += gol.isDebug() ? "ON " : "OFF";
        info += " | EXPORT GIF (G): ";
        info += gol.isExportGif() ? "ON " : "OFF";
        info += gol.isRun() ? " | STOP (SPACE)" : " | START (SPACE)";
        font.FaceSize(10);
        glRasterPos2f(-.95f, -.99f);
        font.Render(info.c_str());

        if(gol.isDebug()) font.FaceSize(8);
        if(!gol.isDebug()) usleep(50000); //not so fast please!

        glfwSwapBuffers(window);
        glfwPollEvents();
    }

    //save gif to file
    if(gol.isExportGif()) {
        std::cout << "saving " << gif.size() << " frames to gol.gif\n";
        gif.back().write("./last.png");
        Magick::writeImages(gif.begin(), gif.end(), gif_file);
    }

    glfwTerminate();
    return 0;
}

Answer 3

Go, ? points

So rather than pin myself down to a particular tiling, I wrote a program that takes a gif or png of a tiling and runs life on it. The gif/png must use a single color for all the tiles.

package main

import (
    "flag"
    "image"
    "image/color"
    "image/gif"
    "image/png"
    "math/rand"
    "os"
    "strings"
)

func main() {
    flag.Parse()
    filename := flag.Args()[0]
    r, err := os.Open(filename)
    if err != nil {
        panic(err)
    }
    var i image.Image
    if strings.HasSuffix(filename, ".gif") {
        i, err = gif.Decode(r)
        if err != nil {
            panic(err)
        }
    }
    if strings.HasSuffix(filename, ".png") {
        i, err = png.Decode(r)
        if err != nil {
            panic(err)
        }
    }

    // find background color
    back := background(i)

    // find connected regions
    n, m := regions(i, back)

    // find edges between regions
    edges := graph(i, m)

    // run life on the tiling
    life(i, n, m, edges)
}

// Find the most-common occurring color.
// This is the "background" color.
func background(i image.Image) color.Color {
    hist := map[color.Color]int{}
    b := i.Bounds()
    for y := b.Min.Y; y < b.Max.Y; y++ {
        for x := b.Min.X; x < b.Max.X; x++ {
            hist[i.At(x, y)]++
        }
    }
    maxn := 0
    var maxc color.Color
    for c, n := range hist {
        if n > maxn {
            maxn = n
            maxc = c
        }
    }
    return maxc
}

// find connected regions.  Returns # of regions and a map from pixels to their region numbers.
func regions(i image.Image, back color.Color) (int, map[image.Point]int) {

    // m maps each background point to a region #
    m := map[image.Point]int{}

    // number regions consecutively
    id := 0

    b := i.Bounds()
    for y := b.Min.Y; y < b.Max.Y; y++ {
        for x := b.Min.X; x < b.Max.X; x++ {
            if i.At(x, y) != back {
                continue
            }
            p := image.Point{x, y}
            if _, ok := m[p]; ok {
                continue // already in a region
            }
            q := []image.Point{p}
            m[p] = id
            k := 0
            for k < len(q) {
                z := q[k]
                k++
                for _, n := range [4]image.Point{{z.X - 1, z.Y}, {z.X + 1, z.Y}, {z.X, z.Y - 1}, {z.X, z.Y + 1}} {
                    if !n.In(b) || i.At(n.X, n.Y) != back {
                        continue
                    }
                    if _, ok := m[n]; ok {
                        continue
                    }
                    m[n] = id
                    q = append(q, n)

                }
            }
            if len(q) < 10 {
                // really tiny region - probably junk in input data
                for _, n := range q {
                    delete(m, n)
                }
                continue
            }
            id++
        }
    }
    return id, m
}

// edge between two regions.  r < s.
type edge struct {
    r, s int
}

// returns a set of edges between regions.
func graph(i image.Image, m map[image.Point]int) map[edge]struct{} {
    // delta = max allowed spacing between adjacent regions
    const delta = 6
    e := map[edge]struct{}{}
    for p, r := range m {
        for dx := -delta; dx <= delta; dx++ {
            for dy := -delta; dy <= delta; dy++ {
                n := image.Point{p.X + dx, p.Y + dy}
                if _, ok := m[n]; !ok {
                    continue
                }
                if m[n] > r {
                    e[edge{r, m[n]}] = struct{}{}
                }
            }
        }
    }
    return e
}

// run life engine
// i = image
// n = # of regions
// m = map from points to their region #
// edges = set of edges between regions
func life(i image.Image, n int, m map[image.Point]int, edges map[edge]struct{}) {
    b := i.Bounds()
    live := make([]bool, n)
    nextlive := make([]bool, n)
    palette := []color.Color{color.RGBA{0, 0, 0, 255}, color.RGBA{128, 0, 0, 255}, color.RGBA{255, 255, 128, 255}} // lines, on, off
    var frames []*image.Paletted
    var delays []int

    // pick random starting lives
    for j := 0; j < n; j++ {
        if rand.Int()%2 == 0 {
            live[j] = true
            nextlive[j] = true
        }
    }
    for round := 0; round < 100; round++ {
        // count live neighbors
        neighbors := make([]int, n)
        for e := range edges {
            if live[e.r] {
                neighbors[e.s]++
            }
            if live[e.s] {
                neighbors[e.r]++
            }
        }

        for j := 0; j < n; j++ {
            nextlive[j] = neighbors[j] == 3 || (live[j] && neighbors[j] == 2)
        }

        // add a frame
        frame := image.NewPaletted(b, palette)
        for y := b.Min.Y; y < b.Max.Y; y++ {
            for x := b.Min.X; x < b.Max.X; x++ {
                frame.SetColorIndex(x, y, 0)
            }
        }
        for p, r := range m {
            if live[r] {
                frame.SetColorIndex(p.X, p.Y, 1)
            } else {
                frame.SetColorIndex(p.X, p.Y, 2)
            }
        }
        frames = append(frames, frame)
        delays = append(delays, 30)

        live, nextlive = nextlive, live
    }

    // write animated gif of result
    w, err := os.Create("animated.gif")
    if err != nil {
        panic(err)
    }
    gif.EncodeAll(w, &gif.GIF{Image: frames, Delay: delays, LoopCount: 100})
    w.Close()
}

Then I just went on the web, grabbed some fun tiling images and ran the program on them.

go run life.go penrose1.go

It generates a file called "animated.gif" which contains a 100-step life simulation of the given tiling.

Standard life:

Penrose tiles:

Above one has an oscillator of period 12.

Above one has an oscillator of period 3.

Answer 4

Java - 11 (ish) points

Comes with fully (mostly) functioning interactive environment!

EDIT

Fatal flaw discovered :(

The path of the alive regions is bounded by the area it is originally formed in. In order to pass the square - double-pentagon barrier, one must have a pre-shaded region on the other side. This is because each shape below it only touches 2 of the regions above it. This means no spaceships or expanding anything, which kind of limits the possibilities. I will try with a different pattern.

BUT!!! if you still want to try it... try it here.

oscillator

Don't know what to call this one - another oscillator

This one looks a little like a ninja star - still life

this one looks like a fly - still life

another oscillator

EDIT

another oscillator found. I am naming this one the eagle.

Hey! another oscillator! (period 4) The windmill.

A 2 period one.

There seems to be a structure that insulates the outside from the inside. This (and the previous example) uses it. The only thing that can break the box is if one of the boundary squares is alive at the beginning (so far). This, by the way, is the blinker - period 2.

I built this in eclipse, and there are multiple files. Here they are.

Main class -

import java.awt.Dimension;
import java.awt.GridBagConstraints;
import java.awt.GridBagLayout;
import java.awt.Point;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.util.ArrayList;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JPanel;
import javax.swing.JTextField;
import javax.swing.Timer;
import javax.swing.event.DocumentEvent;
import javax.swing.event.DocumentListener;

public class Main {

    public static void main(String[] args) {
        new Main();
    }

    Canvas canvas = new Canvas();
    JFrame frame = new JFrame();
    Timer timer;
    ShapeInfo info;
    int[][][] history;
    public Main() {
        JPanel panel = new JPanel();
        panel.setMinimumSize(new Dimension(500,500));
        panel.setLayout(new GridBagLayout());

        frame.setMinimumSize(new Dimension(500,500));
        frame.getContentPane().add(panel);
        frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

        //frame.setResizable(false);
        canvas.setMinimumSize(new Dimension(200,200));
        GridBagConstraints c = new GridBagConstraints();
        c.gridx = 0;
        c.gridy = 2;
        c.weightx = 1;
        c.weighty = 1;
        c.gridwidth = 2;
        c.fill = GridBagConstraints.BOTH;
        panel.add(canvas,c);

        JButton startButton = new JButton();
        startButton.setText("click to start");
        startButton.setMaximumSize(new Dimension(100,50));
        GridBagConstraints g = new GridBagConstraints();
        g.gridx =0;
        g.gridy = 0;
        g.weightx = 1;
        panel.add(startButton,g);

        JButton restartButton = new JButton();
        restartButton.setText("revert");
        GridBagConstraints b = new GridBagConstraints();
        b.gridx = 0;
        b.gridy = 9;
        panel.add(restartButton,b);

        JButton clearButton = new JButton();
        clearButton.setText("Clear");
        GridBagConstraints grid = new GridBagConstraints();
        grid.gridx = 1;
        grid.gridy = 0;
        panel.add(clearButton,grid);

        clearButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                info = new ShapeInfo(canvas.squaresWide,canvas.squaresHigh);
                restart();
            }
        });

        final JTextField scaleFactor = new JTextField();
        scaleFactor.setText("5");
        GridBagConstraints gh = new GridBagConstraints();
        gh.gridx  = 0;
        gh.gridy = 1;
        panel.add(scaleFactor,gh);
        scaleFactor.getDocument().addDocumentListener(new DocumentListener(){

            @Override
            public void changedUpdate(DocumentEvent arg0) {
                doSomething();
            }

            @Override
            public void insertUpdate(DocumentEvent arg0) {
                doSomething();
            }

            @Override
            public void removeUpdate(DocumentEvent arg0) {
                doSomething();
            }
            public void doSomething(){
                try{
                canvas.size = Integer.valueOf(scaleFactor.getText());
                canvas.draw(info.allShapes);
                }
                catch(Exception e){}
            }

        });
        timer = new Timer(1000, listener);
        frame.pack();
        frame.setVisible(true);
        info = new ShapeInfo(canvas.squaresWide, canvas.squaresHigh);
        info.width = canvas.squaresWide;
        info.height = canvas.squaresHigh;
        history = cloneArray(info.allShapes);
        //history[8][11][1] = 1;
        canvas.draw(info.allShapes);
        restartButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                if(timer.isRunning() == true){
                    info.allShapes = cloneArray(history);
                    restart();
                }
            }
        });
        canvas.addMouseListener(new MouseListener(){
            @Override
            public void mouseClicked(MouseEvent e) {
                int x = e.getLocationOnScreen().x - canvas.getLocationOnScreen().x;
                int y = e.getLocationOnScreen().y - canvas.getLocationOnScreen().y;
                Point location = new Point(x,y);
                for(PolygonInfo p:canvas.polygons){
                    if(p.polygon.contains(location)){
                        if(info.allShapes[p.x][p.y][p.position-1] == 1){
                            info.allShapes[p.x][p.y][p.position-1] = 0;
                        }
                        else{
                            info.allShapes[p.x][p.y][p.position-1] = 1;
                        }
                    }
                }
                canvas.draw(info.allShapes);
                history = cloneArray(info.allShapes);
            }
            @Override
            public void mouseEntered(MouseEvent arg0) {
            }
            @Override
            public void mouseExited(MouseEvent arg0) {
            }
            @Override
            public void mousePressed(MouseEvent arg0) { 
            }
            @Override
            public void mouseReleased(MouseEvent arg0) {    
            }
        });
        startButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                timer.start();
            }
        });
    }
    public int[][][] cloneArray(int[][][] array){
        int[][][] newArray = new int[array.length][array[0].length][array[0][0].length];
        for(int x = 0;x<array.length;x++){
            int[][] subArray = array[x];
            for(int y = 0; y < subArray.length;y++){
                int subSubArray[] = subArray[y];
                newArray[x][y] = subSubArray.clone();
            }
        }
        return newArray;
    }
    public void restart(){
        timer.stop();
        canvas.draw(info.allShapes);
    }
    public void setUp(){
        int[] boxes = new int[]{2,3,4,6,7,8};
        for(int box:boxes){
            info.allShapes[8][12][box-1] = 1;
            info.allShapes[9][13][box-1] = 1;
            info.allShapes[8][14][box-1] = 1;
            info.allShapes[9][15][box-1] = 1;
        }
    }
    public void update() {
        ArrayList<Coordinate> dieList = new ArrayList<Coordinate>();
        ArrayList<Coordinate> appearList = new ArrayList<Coordinate>();
        for (int x = 0; x < canvas.squaresWide; x++) {
            for (int y = 0; y < canvas.squaresHigh; y++) {
                for(int position = 0;position <9;position++){
                    int alive = info.allShapes[x][y][position];
                    int touching = info.shapesTouching(x, y, position+1);
                    if(touching!=0){
                    }
                    if(alive == 1){
                        if(touching < 2 || touching > 3){
                            //cell dies
                            dieList.add(new Coordinate(x,y,position));
                        }
                    }
                    else{
                        if(touching == 3){
                            //cell appears
                            appearList.add(new Coordinate(x,y,position));
                        }
                    }
                }
            }
        }
        for(Coordinate die:dieList){
            info.allShapes[die.x][die.y][die.position] = 0;
        }
        for(Coordinate live:appearList){
            info.allShapes[live.x][live.y][live.position] = 1;
        }
    }
    boolean firstDraw = true;
    int ticks = 0;
    ActionListener listener = new ActionListener() {
        @Override
        public void actionPerformed(ActionEvent arg0) {
            canvas.draw(info.allShapes);
            if(ticks !=0){
            update();
            }
            ticks++;
        }
    };
}

Canvas class -

import java.awt.Color;
import java.awt.Graphics;
import java.awt.Polygon;
import java.util.ArrayList;

import javax.swing.JPanel;

public class Canvas extends JPanel {
    private static final long serialVersionUID = 1L;

    public int squaresWide = 30;
    public int squaresHigh = 30;
    public int size = 4;
    ArrayList<PolygonInfo> polygons = new ArrayList<PolygonInfo>();
    boolean drawTessalationOnly = true;
    private int[][][] shapes;

    public void draw(int[][][] shapes2) {
        shapes = shapes2;
        drawTessalationOnly = false;
        this.repaint();
    }

    @Override
    protected void paintComponent(Graphics g) {
        //System.out.println("drawing");
        polygons.clear();
        super.paintComponent(g);
        g.setColor(Color.black);
        // draw tessellation
        for (int x = 0; x < squaresWide; x++) {
            for (int y = 0; y < squaresHigh; y++) {
                for (int position = 1; position <= 9; position++) {
                    // System.out.println("position = " + position);
                    Polygon p = new Polygon();
                    int points = 0;
                    int[] xc = new int[] {};
                    int[] yc = new int[] {};
                    if (position == 1) {
                        xc = new int[] { 0, -2, 0, 2 };
                        yc = new int[] { 2, 0, -2, 0 };
                        points = 4;
                    }
                    if (position == 2) {
                        xc = new int[] { 2, 6, 7, 4, 1 };
                        yc = new int[] { 0, 0, 1, 2, 1 };
                        points = 5;
                    }
                    if (position == 3) {
                        xc = new int[] { 1, 4, 4, 2 };
                        yc = new int[] { 1, 2, 4, 4 };
                        points = 4;
                    }
                    if (position == 4) {
                        xc = new int[] { 4, 4, 7, 6 };
                        yc = new int[] { 4, 2, 1, 4 };
                        points = 4;
                    }
                    if (position == 5) {
                        xc = new int[] { 1, 2, 1, 0, 0 };
                        yc = new int[] { 1, 4, 7, 6, 2 };
                        points = 5;
                    }
                    if (position == 6) {
                        xc = new int[] { 7, 8, 8, 7, 6 };
                        yc = new int[] { 1, 2, 6, 7, 4 };
                        points = 5;
                    }
                    if (position == 7) {
                        xc = new int[] { 4, 2, 1, 4 };
                        yc = new int[] { 4, 4, 7, 6 };
                        points = 4;
                    }
                    if (position == 8) {
                        xc = new int[] { 4, 6, 7, 4 };
                        yc = new int[] { 4, 4, 7, 6 };
                        points = 4;
                    }
                    if (position == 9) {
                        xc = new int[] { 4, 7, 6, 2, 1 };
                        yc = new int[] { 6, 7, 8, 8, 7 };
                        points = 5;
                    }
                    int[] finalX = new int[xc.length];
                    int[] finalY = new int[yc.length];
                    for (int i = 0; i < xc.length; i++) {
                        int xCoord = xc[i];
                        xCoord = (xCoord + (8 * x)) * size;
                        finalX[i] = xCoord;
                    }
                    for (int i = 0; i < yc.length; i++) {
                        int yCoord = yc[i];
                        yCoord = (yCoord + (8 * y)) * size;
                        finalY[i] = yCoord;
                    }
                    p.xpoints = finalX;
                    p.ypoints = finalY;
                    p.npoints = points;
                    polygons.add(new PolygonInfo(p,x,y,position));
                    // for(int i = 0;i<p.npoints;i++){
                    // / System.out.println("(" + p.xpoints[i] + "," +
                    // p.ypoints[i] + ")");
                    // }
                    if (drawTessalationOnly == false) {
                        if (shapes[x][y][position - 1] == 1) {
                            g.fillPolygon(p);
                        } else {
                            g.drawPolygon(p);
                        }
                    } else {
                        g.drawPolygon(p);
                    }
                }

            }
        }
    }
}

ShapeInfo class -

public class ShapeInfo {
    int[][][] allShapes; //first 2 dimensions are coordinates of large square, last is boolean - if shaded
    int width = 20;
    int height = 20;
    public ShapeInfo(int width,int height){
        allShapes = new int[width][height][16];
        for(int[][] i:allShapes){
            for(int[] h:i){
                for(int g:h){
                    g=0;
                }
            }
        }
    }
    public int shapesTouching(int x,int y,int position){
        int t = 0;
        if(x>0 && y >0 && x < width-1 && y < height-1){
        if(position == 1){
            if(allShapes[x][y][2-1] == 1){t++;}
            if(allShapes[x][y][5-1] == 1){t++;}
            if(allShapes[x-1][y][6-1] == 1){t++;}
            if(allShapes[x-1][y][2-1] == 1){t++;}
            if(allShapes[x][y-1][5-1] == 1){t++;}
            if(allShapes[x][y-1][9-1] == 1){t++;}
            if(allShapes[x-1][y-1][9-1] == 1){t++;}
            if(allShapes[x-1][y-1][6-1] == 1){t++;}
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x-1][y][4-1] == 1){t++;}
            if(allShapes[x][y-1][7-1] == 1){t++;}
            if(allShapes[x-1][y-1][8-1] == 1){t++;}
        }
        if(position == 2){
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x][y][4-1] == 1){t++;}
            if(allShapes[x][y][1-1] == 1){t++;}
            if(allShapes[x][y-1][9-1] == 1){t++;}
            if(allShapes[x+1][y][1-1] == 1){t++;}
            if(allShapes[x][y][6-1] == 1){t++;}
            if(allShapes[x][y][5-1] == 1){t++;}
        }
        if(position == 3){
            if(allShapes[x][y][2-1] == 1){t++;}
            if(allShapes[x][y][5-1] == 1){t++;}
            if(allShapes[x][y][4-1] == 1){t++;}
            if(allShapes[x][y][7-1] == 1){t++;}
            if(allShapes[x][y][1-1] == 1){t++;}
            if(allShapes[x][y][8-1] == 1){t++;}
        }
        if(position == 4){
            if(allShapes[x][y][2-1] == 1){t++;}
            if(allShapes[x][y][6-1] == 1){t++;}
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x][y][8-1] == 1){t++;}
            if(allShapes[x][y][7-1] == 1){t++;}
            if(allShapes[x+1][y][1-1] == 1){t++;}
        }
        if(position == 5){
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x][y][7-1] == 1){t++;}
            if(allShapes[x][y][1-1] == 1){t++;}
            if(allShapes[x][y+1][1-1] == 1){t++;}
            if(allShapes[x-1][y][6-1] == 1){t++;}
            if(allShapes[x][y][2-1] == 1){t++;}
            if(allShapes[x][y][9-1] == 1){t++;}
        }
        if(position == 6){
            if(allShapes[x][y][4-1] == 1){t++;}
            if(allShapes[x][y][8-1] == 1){t++;}
            if(allShapes[x+1][y][1-1] == 1){t++;}
            if(allShapes[x+1][y][5-1] == 1){t++;}
            if(allShapes[x+1][y+1][1-1] == 1){t++;}
            if(allShapes[x][y][2-1] == 1){t++;}
            if(allShapes[x][y][9-1] == 1){t++;}
        }
        if(position == 7){
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x][y][8-1] == 1){t++;}
            if(allShapes[x][y][5-1] == 1){t++;}
            if(allShapes[x][y][9-1] == 1){t++;}
            if(allShapes[x][y][4-1] == 1){t++;}
            if(allShapes[x][y+1][1-1] == 1){t++;}
        }
        if(position == 8){
            if(allShapes[x][y][9-1] == 1){t++;}
            if(allShapes[x][y][6-1] == 1){t++;}
            if(allShapes[x][y][7-1] == 1){t++;}
            if(allShapes[x][y][4-1] == 1){t++;}
            if(allShapes[x][y][3-1] == 1){t++;}
            if(allShapes[x+1][y+1][1-1] == 1){t++;}
        }
        if(position == 9){
            if(allShapes[x][y][7-1] == 1){t++;}
            if(allShapes[x][y][8-1] == 1){t++;}
            if(allShapes[x+1][y+1][1-1] == 1){t++;}
            if(allShapes[x][y+1][2-1] == 1){t++;}
            if(allShapes[x][y+1][1-1] == 1){t++;}
            if(allShapes[x][y][6-1] == 1){t++;}
            if(allShapes[x][y][5-1] == 1){t++;}
        }
        }
        return t;
    }
}

PolygonInfo class -

import java.awt.Polygon;

public class PolygonInfo {
    public Polygon polygon;
    public int x;
    public int y;
    public int position;
    public PolygonInfo(Polygon p,int X,int Y,int Position){
        x = X;
        y = Y;
        polygon = p;
        position = Position;
    }
}

and finally... Coordinate class

public class Coordinate {
    int x;
    int y;
    int position;
    public Coordinate(int X,int Y, int Position){
        x=X;
        y=Y;
        position = Position;
    }
}

Answer 5

Python

I place multiple points on a metatile, which is then copied periodically in a rectangular or hexagonal tiling (the metatiles are allowed to overlap). From the set of all points i then compute the Voronoi diagram which makes up my grid.

Some older examples

Random graph, the Delaunay trinagulation is shown which is also used internally to find the neighbours

A periodic tiling which spells GoL

Some more grids showing still lifes

For any such grid there is a huge amount of still lifes with a wide variety of sizes, and some small 2-, 3- or 5-cycle oscillators, but I haven't found any gliders, probably due to the irregularities of the grid. I think about automatizing the search for lifeforms by checking cells for periodic oscillations.

import networkx as nx
from scipy.spatial import Delaunay, Voronoi
from scipy.spatial._plotutils import _held_figure, _adjust_bounds
from numpy import *
import matplotlib.pyplot as plt

# copied from scipy.spatial._plotutils
@_held_figure
def voronoi_plot_2d(vor, ax=None):
    for simplex in vor.ridge_vertices:
        simplex = asarray(simplex)
        if all(simplex >= 0):
            ax.plot(vor.vertices[simplex,0], vor.vertices[simplex,1], 'k-')
    center = vor.points.mean(axis=0)  
    _adjust_bounds(ax, vor.points)
    return ax.figure

def maketilegraph(tile, offsetx, offsety, numx, numy, hexa=0):
    # tile: list of (x,y) coordinates
    # hexa=0: rectangular tiling
    # hexa=1: hexagonal tiling
    R = array([offsetx,0])
    U = array([0,offsety]) - hexa*R/2
    points = concatenate( [tile+n*R for n in range(numx)])
    points = concatenate( [points+n*U for n in range(numy)])

    pos = dict(enumerate(points))
    D = Delaunay(points)

    graph = nx.Graph()
    for tri in D.vertices:
        graph.add_cycle(tri)    
    return graph, pos, Voronoi(points)

def rule(old_state, Nalive):
    if Nalive<2: old_state = 0
    if Nalive==3: old_state = 1
    if Nalive>3: old_state = 0
    return old_state

def propagate(graph):
    for n in graph: # compute the new state
        Nalive = sum([graph.node[m]['alive'] for m in graph.neighbors(n)])
        graph.node[n]['alive_temp'] = rule(graph.node[n]['alive'], Nalive)
    for n in graph: # apply the new state
        graph.node[n]['alive'] = graph.node[n]['alive_temp']

def drawgraph(graph):
    nx.draw_networkx_nodes(graph,pos,
                        nodelist=[n for n in graph if graph.node[n]['alive']],
                        node_color='k', node_size=150)
    # nx.draw_networkx_nodes(graph,pos,
                        # nodelist=[n for n in graph if not graph.node[n]['alive']],
                        # node_color='y', node_size=25, alpha=0.5)
    # nx.draw_networkx_edges(graph,pos, width=1, alpha=0.2, edge_color='b')

##################
# Lets get started
p_alive = 0.4   # initial fill ratio

#tile = random.random((6,2))
a = [.3*exp(2j*pi*n/5) for n in range(5)] +[.5+.5j, 0]
tile = array(zip(real(a), imag(a)))
grid, pos, vor = maketilegraph(tile, 1.,1.,8,8, hexa=1)

for n in grid: # initial fill
    grid.node[n]['alive'] = random.random() < p_alive #random fill
    # grid.node[n]['alive'] = n%5==0 or n%3==0    # periodic fill

for i in range(45):propagate(grid) # run until convergence

for i in range(7):
    print i
    voronoi_plot_2d(vor)
    drawgraph(grid)
    plt.axis('off')
    plt.savefig('GoL %.3d.png'%i, bbox_inches='tight')
    plt.close()
    propagate(grid)

Answer 6

Javascript [25+?]

http://jsfiddle.net/Therm/dqb2h2oc/

House tessellations! There are two shapes: "House" and "Upsidedown House", each with 7 neighbors.

Currently I have a score of 25.

still life                  : +2
2-stage oscillator "beacon" : +3  (Credit to isaacg)
Spaceship "Toad"            : +10 (Credit to isaacg)
Glider                      : +10 (Credit to Martin Büttner)

Naming rights for patterns up for grabs if you find them :p

Still life - Star

2 Stage oscillator - "Beacon" : Found by isaacg

Spaceship - "Toad": Found by isaacg

Glider - Unnamed: Found by Martin Büttner

The fiddle is currently set to randomly populate the world as an initial state.

Code:

// An animation similar to Conway's Game of Life, using house-tessellations.
// B2/S23

var world;
var worldnp1;
var intervalTime = 2000;

var canvas = document.getElementById('c');
var context = canvas.getContext('2d');

var x = 32;
var y = 32;

var width = 20; // width of house
var height = 15; // height of house base
var theight = 5; // height of house roof
var deadC = '#3300FF';
var aliveC = '#00CCFF';

function initWorld() {
    world = new Array(x * y);

    /* Still life - box
        world[x/2 * y + y/2 + 1] = 1;
        world[x/2 * y + y/2] = 1;
        world[x/2 * y + y/2 + y] = 1;
        world[x/2 * y + y/2 + y + 1] = 1;
    */

    /* Still life - House
        world[x/2 * y + y/2 - y] = 1;
        world[x/2 * y + y/2 + 1] = 1;
        world[x/2 * y + y/2 - 1] = 1;
        world[x/2 * y + y/2 + y] = 1;
        world[x/2 * y + y/2 + y+1] = 1;
    */

    /* Oscillator on an infinite plane :(
    for(var i=0; i<y; i++) {
        world[y/2 * y + i] = 1 ^ (i%2);
        world[y/2 * y + y + i] = 1 ^ (i%2);
    } */

    // Random state 
    for(var i=0; i<x*y; i++) {
        world[i] = Math.round(Math.random());
    }

    drawGrid();
}

animateWorld = function () {
    computeNP1();
    drawGrid();
};

function computeNP1() {
    worldnp1 = new Array(x * y);
    var buddies;
    for (var i = 0; i < x * y; i++) {
        buddies = getNeighbors(i);
        var aliveBuddies = 0;
        for (var j = 0; j < buddies.length; j++) {
            if (world[buddies[j]]) {
                aliveBuddies++;
            }
        }
        if (world[i]) {
            if (aliveBuddies === 2 || aliveBuddies === 3) {
                worldnp1[i] = 1;
            }
        }
        else {
            if (aliveBuddies === 3) {
                worldnp1[i] = 1;
            }
        }
    }
    world = worldnp1.slice(0);
}

function drawGrid() {
    var dx = 0;
    var dy = 0;
    var shiftLeft = 0;
    var pointDown = 0;
    for (var i = 0; i < y; i++) {
        // yay XOR
        shiftLeft ^= pointDown;
        pointDown ^= 1;
        if (shiftLeft) {
            dx -= width / 2;
        }
        for (var j = 0; j < x; j++) {
            var c = world[i * y + j] ? aliveC : deadC ;
            draw5gon(dx, dy, pointDown, c);
            outline5gon(dx, dy, pointDown);
            dx += width;
        }
        dx = 0;
        if (pointDown) {
            dy += 2 * height + theight;
        }
    }
}

function getNeighbors(i) {
    neighbors = [];

    // Everybody has a L/R neighbor
    if (i % x !== 0) {
        neighbors.push(i - 1);
    }
    if (i % x != x - 1) {
        neighbors.push(i + 1);
    }

    // Everybody has "U/D" neighbor
    neighbors.push(i - x);
    neighbors.push(i + x);

    // Down facers (R1)
    if (Math.floor(i / x) % 4 === 0) {
        if (i % x !== 0) {
            neighbors.push(i - x - 1);
        }
        if (i % x != x - 1) {
            neighbors.push(i - x + 1);
            neighbors.push(i + x + 1);
        }
    }

    // Up facers (R2)
    else if (Math.floor(i / x) % 4 === 1) {
        if (i % x !== 0) {
            neighbors.push(i - x - 1);
            neighbors.push(i + x - 1);
        }
        if (i % x != x - 1) {
            neighbors.push(i + x + 1);
        }
    }

    // Down facers (R3)
    else if (Math.floor(i / x) % 4 === 2) {
        if (i % x !== 0) {
            neighbors.push(i - x - 1);
            neighbors.push(i + x - 1);
        }
        if (i % x != x - 1) {
            neighbors.push(i - x + 1);
        }
    }

    // Up facers (R4)
    // else if ( Math.floor(i/x) % 4 === 3 )
    else {
        if (i % x !== 0) {
            neighbors.push(i + x - 1);
        }
        if (i % x != x - 1) {
            neighbors.push(i - x + 1);
            neighbors.push(i + x + 1);
        }
    }

    return neighbors.filter(function (val, ind, arr) {
        return (0 <= val && val < x * y);
    });
}

// If pointdown, x,y refer to top left corner
// If not pointdown, x,y refers to lower left corner
function draw5gon(x, y, pointDown, c) {
    if (pointDown) {
        drawRect(x, y, width, height, c);
        drawTriangle(x, y + height, x + width, y + height, x + width / 2, y + height + theight);
    } else {
        drawRect(x, y - height, width, height, c);
        drawTriangle(x, y - height, x + width / 2, y - height - theight, x + width, y - height);
    }
}

function outline5gon(x, y, pointDown) {
    context.beginPath();
    context.moveTo(x, y);
    if (pointDown) {
        context.lineTo(x + width, y);
        context.lineTo(x + width, y + height);
        context.lineTo(x + width / 2, y + height + theight);
        context.lineTo(x, y + height);
    } else {
        context.lineTo(x, y - height);
        context.lineTo(x + width / 2, y - height - theight);
        context.lineTo(x + width, y - height);
        context.lineTo(x + width, y);
    }
    context.lineWidth = 3;
    context.strokeStyle = '#000000';
    context.stroke();
}

function drawRect(x, y, w, h, c) {
    context.fillStyle = c;
    context.fillRect(x, y, w, h);
}

function drawTriangle(x1, y1, x2, y2, x3, y3, c) {
    context.beginPath();
    context.moveTo(x1, y1);
    context.lineTo(x2, y2);
    context.lineTo(x3, y3);
    context.fillStyle = c;
    context.fill();
}

$(document).ready(function () {
    initWorld();
    intervalID = window.setInterval(animateWorld, intervalTime);
});

Answer 7

Javascript [27+?]

http://jsfiddle.net/Therm/5n53auja/

Round 2! Now with hexagons, squares, and triangles. And interactivity

This version supports clicking tiles to toggle their state, for you pattern hunters out there. Note: Some of the click handling may be a bit wonky, especially for low values of s, as click events are tracked as integers but calculations are done with floating point values

Current score - 24

Still life           : +2
Period 2 oscillator  : +3
Period 4 oscillator  : +3
Period 6 oscillator  : +3
Period 10 oscillator : +3
Period 12 oscillator : +3
Spaceship            : +10

Period 4 oscillator : Found by Martin Büttner

Period 6 oscillator : Found by Martin Büttner

Period 10 oscillator: Found by Martin Büttner

Period 12 oscillator : Found by Martin Büttner

Period 20 spaceship : Found by Martin Büttner

Answer 8

Cairo pentagonal tiling (+ generic framework), 17+ points

This tiling is surprisingly easy to draw: the key is that the only irrational number which is important for drawing it, sqrt(3), is very close to the rational number 7/4, which has the added bonus that if you subtract 1 from the numerator and denominator you get 6/3 = 2, so that the non-axis-aligned lines are nicely symmetric.

If you want grid paper, I've created a PostScript gist for A4. Feel free to fork it for other paper sizes.

The code is generic enough to support other tilings. The interface which needs to be implemented is:

import java.util.Set;

interface Tiling<Cell> {
    /** Calculates the neighbourhood, which should not include the cell itself. */
    public Set<Cell> neighbours(Cell cell);
    /** Gets an array {xs, ys} of polygon vertices. */
    public int[][] bounds(Cell cell);
    /** Starting cell for random generation. This doesn't need to be consistent. */
    public Cell initialCell();
    /** Allows exclusion of common oscillations in random generation. */
    public boolean isInterestingOscillationPeriod(int period);
    /** Parse command-line input. */
    public Set<Cell> parseCells(String[] data);
}

Then the Cairo tiling is:

import java.awt.Point;
import java.util.*;

/**
 * http://en.wikipedia.org/wiki/Cairo_pentagonal_tiling
 */
class CairoTiling implements Tiling<Point> {
    private static final int[][] SHAPES_X = new int[][] {
        { 0, 4, 11, 11, 4 },
        { 11, 4, 8, 14, 18 },
        { 11, 18, 14, 8, 4 },
        { 22, 18, 11, 11, 18 }
    };
    private static final int[][] SHAPES_Y = new int[][] {
        { 0, 7, 3, -3, -7 },
        { 3, 7, 14, 14, 7 },
        { -3, -7, -14, -14, -7 },
        { 0, -7, -3, 3, 7 }
    };

    public Set<Point> neighbours(Point cell) {
        Set<Point> neighbours = new HashSet<Point>();
        int exclx = (cell.y & 1) == 0 ? -1 : 1;
        int excly = (cell.x & 1) == 0 ? -1 : 1;
        for (int dx = -1; dx <= 1; dx++) {
            for (int dy = -1; dy <= 1; dy++) {
                if (dx == 0 && dy == 0) continue;
                if (dx == exclx && dy == excly) continue;
                neighbours.add(new Point(cell.x + dx, cell.y + dy));
            }
        }

        return neighbours;
    }

    public int[][] bounds(Point cell) {
        int x = cell.x, y = cell.y;

        int[] xs = SHAPES_X[(x & 1) + 2 * (y & 1)].clone();
        int[] ys = SHAPES_Y[(x & 1) + 2 * (y & 1)].clone();
        int xoff = 7 * (x & ~1) + 7 * (y & ~1);
        int yoff = 7 * (x & ~1) - 7 * (y & ~1);

        for (int i = 0; i < 5; i++) {
            xs[i] += xoff;
            ys[i] += yoff;
        }

        return new int[][] { xs, ys };
    }

    public Point initialCell() { return new Point(0, 0); }

    public boolean isInterestingOscillationPeriod(int period) {
        // Period 6 oscillators are extremely common, and period 2 fairly common.
        return period != 2 && period != 6;
    }

    public Set<Point> parseCells(String[] data) {
        if ((data.length & 1) == 1) throw new IllegalArgumentException("Expect pairs of integers");

        Set<Point> cells = new HashSet<Point>();
        for (int i = 0; i < data.length; i += 2) {
            cells.add(new Point(Integer.parseInt(data[i]), Integer.parseInt(data[i + 1])));
        }

        return cells;
    }
}

and the control code is

import java.awt.*;
import java.awt.image.*;
import java.io.*;
import java.util.*;
import java.util.List;
import javax.imageio.*;
import javax.imageio.metadata.*;
import javax.imageio.stream.*;
import org.w3c.dom.Node;

/**
 * Implements a Life-like cellular automaton on a generic grid.
 * http://codegolf.stackexchange.com/q/35827/194
 *
 * TODOs:
 *  - Allow a special output format for gliders which moves the bounds at an appropriate speed and doesn't extend the last frame
 *  - Allow option to control number of generations
 */
public class GenericLife {
    private static final Color GRIDCOL = new Color(0x808080);
    private static final Color DEADCOL = new Color(0xffffff);
    private static final Color LIVECOL = new Color(0x0000ff);

    private static final int MARGIN = 15;

    private static void usage() {
        System.out.println("Usage: java GenericLife <tiling> [<output.gif> <cell-data>]");
        System.out.println("For CairoTiling, cell data is pairs of integers");
        System.out.println("For random search, supply just the tiling name");
        System.exit(1);
    }

    // Unchecked warnings due to using reflection to instantation tiling over unknown cell type
    @SuppressWarnings("unchecked")
    public static void main(String[] args) throws Exception {
        if (args.length == 0 || args[0].equals("--help")) usage();

        Tiling tiling = (Tiling)Class.forName(args[0]).newInstance();
        if (args.length > 1) {
            String[] cellData = new String[args.length - 2];
            System.arraycopy(args, 2, cellData, 0, cellData.length);
            Set alive;
            try { alive = tiling.parseCells(cellData); }
            catch (Exception ex) { usage(); return; }

            createAnimatedGif(args[1], tiling, evolve(tiling, alive, 100));
        }
        else search(tiling);
    }

    private static <Cell> void search(Tiling<Cell> tiling) throws IOException {
        while (true) {
            // Build a starting generation within a certain radius of the initial cell.
            // This is a good place to tweak.
            Set<Cell> alive = new HashSet<Cell>();
            double density = Math.random();
            Set<Cell> visited = new HashSet<Cell>();
            Set<Cell> boundary = new HashSet<Cell>();
            boundary.add(tiling.initialCell());
            for (int r = 0; r < 10; r++) {
                visited.addAll(boundary);
                Set<Cell> nextBoundary = new HashSet<Cell>();
                for (Cell cell : boundary) {
                    if (Math.random() < density) alive.add(cell);
                    for (Cell neighbour : tiling.neighbours(cell)) {
                        if (!visited.contains(neighbour)) nextBoundary.add(neighbour);
                    }
                }

                boundary = nextBoundary;
            }

            final int MAX = 1000;
            List<Set<Cell>> gens = evolve(tiling, alive, MAX);
            // Long-lived starting conditions might mean a glider, so are interesting.
            boolean interesting = gens.size() == MAX;
            String desc = "gens-" + MAX;
            if (!interesting) {
                // We hit some oscillator - but was it an interesting one?
                int lastGen = gens.size() - 1;
                gens = evolve(tiling, gens.get(lastGen), gens.size());
                if (gens.size() > 1) {
                    int period = gens.size() - 1;
                    desc = "oscillator-" + period;
                    interesting = tiling.isInterestingOscillationPeriod(period);
                    System.out.println("Oscillation of period " + period);
                }
                else {
                    String result = gens.get(0).isEmpty() ? "Extinction" : "Still life";
                    System.out.println(result + " at gen " + lastGen);
                }
            }

            if (interesting) {
                String filename = System.getProperty("java.io.tmpdir") + "/" + tiling.getClass().getSimpleName() + "-" + System.nanoTime() + "-" + desc + ".gif";
                createAnimatedGif(filename, tiling, gens);
                System.out.println("Wrote " + gens.size() + " generations to " + filename);
            }
        }
    }

    private static <Cell> List<Set<Cell>> evolve(Tiling<Cell> tiling, Set<Cell> gen0, int numGens) {
        Map<Set<Cell>, Integer> firstSeen = new HashMap<Set<Cell>, Integer>();
        List<Set<Cell>> gens = new ArrayList<Set<Cell>>();
        gens.add(gen0);
        firstSeen.put(gen0, 0);

        Set<Cell> alive = gen0;
        for (int gen = 1; gen < numGens; gen++) {
            if (alive.size() == 0) break;

            Set<Cell> nextGen = nextGeneration(tiling, alive);
            Integer prevSeen = firstSeen.get(nextGen);
            if (prevSeen != null) {
                if (gen - prevSeen > 1) gens.add(nextGen); // Finish the loop.
                break;
            }

            alive = nextGen;
            gens.add(alive);
            firstSeen.put(alive, gen);
        }

        return gens;
    }

    private static <Cell> void createAnimatedGif(String filename, Tiling<Cell> tiling, List<Set<Cell>> gens) throws IOException {
        OutputStream out = new FileOutputStream(filename);
        ImageWriter imgWriter = ImageIO.getImageWritersByFormatName("gif").next();
        ImageOutputStream imgOut = ImageIO.createImageOutputStream(out);
        imgWriter.setOutput(imgOut);
        imgWriter.prepareWriteSequence(null);

        Rectangle bounds = bbox(tiling, gens);
        Set<Cell> gen0 = gens.get(0);
        int numGens = gens.size();

        for (int gen = 0; gen < numGens; gen++) {
            Set<Cell> alive = gens.get(gen);

            // If we have an oscillator which loops cleanly back to the start, skip the last frame.
            if (gen > 0 && alive.equals(gen0)) break;

            writeGifFrame(imgWriter, render(tiling, bounds, alive), gen == 0, gen == numGens - 1);
        }

        imgWriter.endWriteSequence();
        imgOut.close();
        out.close();
    }

    private static <Cell> Rectangle bbox(Tiling<Cell> tiling, Collection<? extends Collection<Cell>> gens) {
        Rectangle bounds = new Rectangle(-1, -1);
        Set<Cell> allGens = new HashSet<Cell>();
        for (Collection<Cell> gen : gens) allGens.addAll(gen);
        for (Cell cell : allGens) {
            int[][] cellBounds = tiling.bounds(cell);
            int[] xs = cellBounds[0], ys = cellBounds[1];
            for (int i = 0; i < xs.length; i++) bounds.add(xs[i], ys[i]);
        }

        bounds.grow(MARGIN, MARGIN);
        return bounds;
    }

    private static void writeGifFrame(ImageWriter imgWriter, BufferedImage img, boolean isFirstFrame, boolean isLastFrame) throws IOException {
        IIOMetadata metadata = imgWriter.getDefaultImageMetadata(new ImageTypeSpecifier(img), null);

        String metaFormat = metadata.getNativeMetadataFormatName();
        Node root = metadata.getAsTree(metaFormat);

        IIOMetadataNode grCtlExt = findOrCreateNode(root, "GraphicControlExtension");
        grCtlExt.setAttribute("delayTime", isLastFrame ? "1000" : "30"); // Extra delay for last frame
        grCtlExt.setAttribute("disposalMethod", "doNotDispose");

        if (isFirstFrame) {
            // Configure infinite looping.
            IIOMetadataNode appExts = findOrCreateNode(root, "ApplicationExtensions");
            IIOMetadataNode appExt = findOrCreateNode(appExts, "ApplicationExtension");
            appExt.setAttribute("applicationID", "NETSCAPE");
            appExt.setAttribute("authenticationCode", "2.0");
            appExt.setUserObject(new byte[] { 1, 0, 0 });
        }

        metadata.setFromTree(metaFormat, root);
        imgWriter.writeToSequence(new IIOImage(img, null, metadata), null);
    }

    private static IIOMetadataNode findOrCreateNode(Node parent, String nodeName) {
        for (Node child = parent.getFirstChild(); child != null; child = child.getNextSibling()) {
            if (child.getNodeName().equals(nodeName)) return (IIOMetadataNode)child;
        }

        IIOMetadataNode node = new IIOMetadataNode(nodeName);
        parent.appendChild(node);
        return node ;
    }

    private static <Cell> Set<Cell> nextGeneration(Tiling<Cell> tiling, Set<Cell> gen) {
        Map<Cell, Integer> neighbourCount = new HashMap<Cell, Integer>();
        for (Cell cell : gen) {
            for (Cell neighbour : tiling.neighbours(cell)) {
                Integer curr = neighbourCount.get(neighbour);
                neighbourCount.put(neighbour, 1 + (curr == null ? 0 : curr.intValue()));
            }
        }

        Set<Cell> nextGen = new HashSet<Cell>();
        for (Map.Entry<Cell, Integer> e : neighbourCount.entrySet()) {
            if (e.getValue() == 3 || (e.getValue() == 2 && gen.contains(e.getKey()))) {
                nextGen.add(e.getKey());
            }
        }

        return nextGen;
    }

    private static <Cell> BufferedImage render(Tiling<Cell> tiling, Rectangle bounds, Collection<Cell> alive) {
        // Create a suitable paletted image
        int width = bounds.width;
        int height = bounds.height;
        byte[] data = new byte[width * height];
        int[] pal = new int[]{ GRIDCOL.getRGB(), DEADCOL.getRGB(), LIVECOL.getRGB() };
        ColorModel colourModel = new IndexColorModel(8, pal.length, pal, 0, false, -1, DataBuffer.TYPE_BYTE);
        DataBufferByte dbb = new DataBufferByte(data, width * height);
        WritableRaster raster = Raster.createPackedRaster(dbb, width, height, width, new int[]{0xff}, new Point(0, 0));
        BufferedImage img = new BufferedImage(colourModel, raster, true, null);
        Graphics g = img.createGraphics();

        // Render the tiling.
        // We assume that either one of the live cells or the "initial cell" is in bounds.
        Set<Cell> visited = new HashSet<Cell>();
        Set<Cell> unvisited = new HashSet<Cell>(alive);
        unvisited.add(tiling.initialCell());
        while (!unvisited.isEmpty()) {
            Iterator<Cell> it = unvisited.iterator();
            Cell current = it.next();
            it.remove();
            visited.add(current);

            Rectangle cellBounds = new Rectangle(-1, -1);
            int[][] cellVertices = tiling.bounds(current);
            int[] xs = cellVertices[0], ys = cellVertices[1];
            for (int i = 0; i < xs.length; i++) {
                cellBounds.add(xs[i], ys[i]);
                xs[i] -= bounds.x;
                ys[i] -= bounds.y;
            }

            if (!bounds.intersects(cellBounds)) continue;

            g.setColor(alive.contains(current) ? LIVECOL : DEADCOL);
            g.fillPolygon(xs, ys, xs.length);
            g.setColor(GRIDCOL);
            g.drawPolygon(xs, ys, xs.length);

            for (Cell neighbour : tiling.neighbours(current)) {
                if (!visited.contains(neighbour)) unvisited.add(neighbour);
            }
        }

        return img;
    }
}

Any vertex generates a still life (2 points):

java GenericLife CairoTiling stilllife.gif 0 0 0 1 1 1 3 2 3 3 4 2 4 3

Oscillators (15 points): clockwise from top-left we have orders 2, 3, 4, 6, 11, 12.

Answer 9

Rhombille (30+ points)

This grid has quite high connectivity (each cell has 10 neighbours), and curiously this seems to contribute more effectively to birth than to death. Most random grids seem to trigger infinite growth (25 points); e.g. this 5-cell starting position:

evolves over 300 generations into something enormous:

and the population grows quadratically with the generation for at least 3000 generations.

Perhaps this is why I've only found one oscillator, of period 2 (3 points):

As for still life (2 points): take any 4 cells around a single vertex.

The code (use with the generic framework and AbstractLattice classes I posted in earlier answers):

public class Rhombille extends AbstractLattice {
    public Rhombille() {
        super(14, 0, 7, 12, new int[][] {
                {0, 7, 14, 7},
                {0, 7, 7, 0},
                {7, 14, 14, 7}
            }, new int[][] {
                {0, 4, 0, -4},
                {0, -4, -12, -8},
                {-4, 0, -8, -12}
            });
    }

    @Override
    public boolean isInterestingOscillationPeriod(int period) {
        return period != 2;
    }
}

Answer 10

Rhombitrihexagonal tiling, 17+ points

As requested by Martin Büttner.

Still life (2 points):

Oscillators of periods (clockwise from top-left) 2, 4, 5, 6, 11 (15 points):

In general an oscillator has a set of cells which change (the core), a set of cells which neighbour the core (the cladding), and a set of cells which keep the cladding from changing (the support). With this tiling, the support of the oscillators can sometimes overlap: e.g.

If the 4-oscillator were removed, the support of the 5-oscillator would fail and it would eventually evolve into a 2-oscillator. But if the 5-oscillator were removed, the support of the 4-oscillator would simply add one hex and stabilise, so this isn't really a 20-oscillator.

---

The code which implements this tiling is extremely generic: building on my experience with an aperiodic tiling, I realised that expanding to a known boundary and doing a lookup by vertex is a very flexible technique, albeit possibly not efficient for simple lattices. But since we're interested in more complex lattices, I've taken that approach here.

Every periodic tiling is a lattice, and it's possible to identify a fundamental unit (in the case of this tiling it's a hexagon, two triangles, and three squares) which is repeated along two axes. Then just supply the axis offsets and the coordinates of the primitive cells of a fundamental unit and you're done.

All of this code can be downloaded as zip at https://gist.github.com/pjt33/becd56784480ddd751bf , and that also includes a GenericLifeGui which I haven't posted on this page.

public class Rhombitrihexagonal extends AbstractLattice {
    public Rhombitrihexagonal() {
        super(22, 0, 11, 19, new int[][] {
                {-7, 0, 7, 7, 0, -7},
                {0, 4, 11, 7},
                {7, 11, 15},
                {7, 15, 15, 7},
                {7, 15, 11},
                {7, 11, 4, 0},
            }, new int[][] {
                {4, 8, 4, -4, -8, -4},
                {8, 15, 11, 4},
                {4, 11, 4},
                {4, 4, -4, -4},
                {-4, -4, -11},
                {-4, -11, -15, -8},
            });
    }

    @Override
    public boolean isInterestingOscillationPeriod(int period) {
        return period != 2 && period != 4 && period != 5 && period != 6 && period != 10 && period != 12 && period != 15 && period != 30;
    }
}

The support for this is my previously posted generic framework plus the AbstractLattice class:

import java.awt.Point;
import java.util.*;

public abstract class AbstractLattice implements Tiling<AbstractLattice.LatticeCell> {
    // Use the idea of expansion and vertex mapping from my earlier aperiod tiling implementation.
    private Map<Point, Set<LatticeCell>> vertexNeighbourhood = new HashMap<Point, Set<LatticeCell>>();
    private int scale = -1;

    // Geometry
    private final int dx0, dy0, dx1, dy1;
    private final int[][] xs;
    private final int[][] ys;

    protected AbstractLattice(int dx0, int dy0, int dx1, int dy1, int[][] xs, int[][] ys) {
        this.dx0 = dx0;
        this.dy0 = dy0;
        this.dx1 = dx1;
        this.dy1 = dy1;
        // Assume sensible subclasses, so no need to clone the arrays to prevent modification.
        this.xs = xs;
        this.ys = ys;
    }

    private void expand() {
        scale++;
        // We want to enumerate all lattice cells whose extreme coordinate is +/- scale.
        // Corners:
        insertLatticeNeighbourhood(-scale, -scale);
        insertLatticeNeighbourhood(-scale, scale);
        insertLatticeNeighbourhood(scale, -scale);
        insertLatticeNeighbourhood(scale, scale);

        // Edges:
        for (int i = -scale + 1; i < scale; i++) {
            insertLatticeNeighbourhood(-scale, i);
            insertLatticeNeighbourhood(scale, i);
            insertLatticeNeighbourhood(i, -scale);
            insertLatticeNeighbourhood(i, scale);
        }
    }

    private void insertLatticeNeighbourhood(int x, int y) {
        for (int sub = 0; sub < xs.length; sub++) {
            LatticeCell cell = new LatticeCell(x, y, sub);
            int[][] bounds = bounds(cell);
            for (int i = 0; i < bounds[0].length; i++) {
                Point p = new Point(bounds[0][i], bounds[1][i]);

                Set<LatticeCell> adj = vertexNeighbourhood.get(p);
                if (adj == null) vertexNeighbourhood.put(p,  adj = new HashSet<LatticeCell>());
                adj.add(cell);
            }
        }
    }

    public Set<LatticeCell> neighbours(LatticeCell cell) {
        Set<LatticeCell> rv = new HashSet<LatticeCell>();

        // +1 because we will border cells from the next scale.
        int requiredScale = Math.max(Math.abs(cell.x), Math.abs(cell.y)) + 1;
        while (scale < requiredScale) expand();

        int[][] bounds = bounds(cell);
        for (int i = 0; i < bounds[0].length; i++) {
            Point p = new Point(bounds[0][i], bounds[1][i]);
            Set<LatticeCell> adj = vertexNeighbourhood.get(p);
            rv.addAll(adj);
        }

        rv.remove(cell);
        return rv;
    }

    public int[][] bounds(LatticeCell cell) {
        int[][] bounds = new int[2][];
        bounds[0] = xs[cell.sub].clone();
        bounds[1] = ys[cell.sub].clone();
        for (int i = 0; i < bounds[0].length; i++) {
            bounds[0][i] += cell.x * dx0 + cell.y * dx1;
            bounds[1][i] += cell.x * dy0 + cell.y * dy1;
        }

        return bounds;
    }

    public LatticeCell initialCell() {
        return new LatticeCell(0, 0, 0);
    }

    public abstract boolean isInterestingOscillationPeriod(int period);

    public Set<LatticeCell> parseCells(String[] data) {
        Set<LatticeCell> rv = new HashSet<LatticeCell>();
        if (data.length % 3 != 0) throw new IllegalArgumentException("Data should come in triples");
        for (int i = 0; i < data.length; i += 3) {
            if (data[i + 2].length() != 1) throw new IllegalArgumentException("Third data item should be a single letter");
            rv.add(new LatticeCell(Integer.parseInt(data[i]), Integer.parseInt(data[i + 1]), data[i + 2].charAt(0) - 'A'));
        }
        return rv;
    }

    public String format(Set<LatticeCell> cells) {
        StringBuilder sb = new StringBuilder();
        for (LatticeCell cell : cells) {
            if (sb.length() > 0) sb.append(' ');
            sb.append(cell.x).append(' ').append(cell.y).append(' ').append((char)(cell.sub + 'A'));
        }

        return sb.toString();
    }

    static class LatticeCell {
        public final int x, y, sub;

        LatticeCell(int x, int y, int sub) {
            this.x = x;
            this.y = y;
            this.sub = sub;
        }

        @Override
        public int hashCode() {
            return (x * 0x100025) + (y * 0x959) + sub;
        }

        @Override
        public boolean equals(Object obj) {
            if (!(obj instanceof LatticeCell)) return false;
            LatticeCell other = (LatticeCell)obj;
            return x == other.x && y == other.y && sub == other.sub;
        }

        @Override
        public String toString() {
            return x + " " + y + " " + (char)('A' + sub);
        }
    }
}

Answer 11

Aperiodic Labyrinth tiling (45+ points)

This uses the generic framework from my earlier answer.

Still life (2 points):

Oscillator (3 points):

This oscillator is extremely common, turning up in the result of most random starting points.

Code:

import java.awt.Point;
import java.util.*;

public class LabyrinthTiling implements Tiling<String> {
    private Map<Point, Point> internedPoints = new HashMap<Point, Point>();
    private Map<String, Set<Point>> vertices = new HashMap<String, Set<Point>>();
    private Map<Point, Set<String>> tris = new HashMap<Point, Set<String>>();

    private int level = 0;
    // 3^level
    private int scale = 1;

    public LabyrinthTiling() {
        linkSymmetric("", new Point(-8, 0));
        linkSymmetric("", new Point(8, 0));
        linkSymmetric("", new Point(0, 14));
    }

    private void linkSymmetric(String suffix, Point p) {
        int ay = Math.abs(p.y);
        link("+" + suffix, new Point(p.x, ay));
        link("-" + suffix, new Point(p.x, -ay));
    }

    private void link(String tri, Point p) {
        Point p2 = internedPoints.get(p);
        if (p2 == null) internedPoints.put(p, p);
        else p = p2;

        Set<Point> ps = vertices.get(tri);
        if (ps == null) vertices.put(tri, ps = new HashSet<Point>());

        Set<String> ts = tris.get(p);
        if (ts == null) tris.put(p, ts = new HashSet<String>());

        ps.add(p);
        ts.add(tri);
    }

    private void expand() {
        level++;
        scale *= 3;
        subdivideEq("", new Point(-8 * scale, 0), new Point(8 * scale, 0), new Point(0, 14 * scale), level, true);
    }

    private static Point avg(Point p0, Point p1, Point p2) {
        return new Point((p0.x + p1.x + p2.x) / 3, (p0.y + p1.y + p2.y) / 3);
    }

    private void subdivideEq(String suffix, Point p0, Point p1, Point p2, int level, boolean skip0) {
        if (level == 0) {
            linkSymmetric(suffix, p0);
            linkSymmetric(suffix, p1);
            linkSymmetric(suffix, p2);
            return;
        }

        Point p01 = avg(p0, p0, p1), p10 = avg(p0, p1, p1);
        Point p02 = avg(p0, p0, p2), p20 = avg(p0, p2, p2);
        Point p12 = avg(p1, p1, p2), p21 = avg(p1, p2, p2);
        Point c = avg(p0, p1, p2);
        level--;

        if (!skip0) subdivideEq(suffix + "0", p01, p10, c, level, false);
        subdivideIso(suffix + "1", p0, c, p01, level);
        subdivideIso(suffix + "2", p0, c, p02, level);
        subdivideEq(suffix + "3", p02, c, p20, level, false);
        subdivideIso(suffix + "4", p2, c, p20, level);
        subdivideIso(suffix + "5", p2, c, p21, level);
        subdivideEq(suffix + "6", c, p12, p21, level, false);
        subdivideIso(suffix + "7", p1, c, p12, level);
        subdivideIso(suffix + "8", p1, c, p10, level);
    }

    private void subdivideIso(String suffix, Point p0, Point p1, Point p2, int level) {
        if (level == 0) {
            linkSymmetric(suffix, p0);
            linkSymmetric(suffix, p1);
            linkSymmetric(suffix, p2);
            return;
        }

        Point p01 = avg(p0, p0, p1), p10 = avg(p0, p1, p1);
        Point p02 = avg(p0, p0, p2), p20 = avg(p0, p2, p2);
        Point p12 = avg(p1, p1, p2), p21 = avg(p1, p2, p2);
        Point c = avg(p0, p1, p2);
        level--;

        subdivideIso(suffix + "0", p0, p01, p02, level);
        subdivideEq(suffix + "1", p01, p02, p20, level, false);
        subdivideIso(suffix + "2", p01, p2, p20, level);
        subdivideIso(suffix + "3", p01, p2, c, level);
        subdivideIso(suffix + "4", p01, p10, c, level);
        subdivideIso(suffix + "5", p10, p2, c, level);
        subdivideIso(suffix + "6", p10, p2, p21, level);
        subdivideEq(suffix + "7", p10, p12, p21, level, false);
        subdivideIso(suffix + "8", p1, p10, p12, level);
    }

    public Set<String> neighbours(String cell) {
        Set<String> rv = new HashSet<String>();

        Set<Point> cellVertices;
        while ((cellVertices = vertices.get(cell)) == null) expand();
        for (Point p : cellVertices) {
            // If the point is on the edge of the current level, we need to expand once more.
            if (Math.abs(p.x) / 8 + Math.abs(p.y) / 14 == scale) expand();

            Set<String> adj = tris.get(p);
            rv.addAll(adj);
        }

        rv.remove(cell);
        return rv;
    }

    public int[][] bounds(String cell) {
        Set<Point> cellVertices;
        while ((cellVertices = vertices.get(cell)) == null) expand();

        int[][] bounds = new int[2][3];
        int off = 0;
        for (Point p : cellVertices) {
            bounds[0][off] = p.x;
            bounds[1][off] = p.y;
            off++;
        }

        return bounds;
    }

    public String initialCell() {
        return "+";
    }

    public boolean isInterestingOscillationPeriod(int period) {
        return period != 4;
    }

    public Set<String> parseCells(String[] data) {
        Set<String> rv = new HashSet<String>();
        for (String cell : data) rv.add(cell);
        return rv;
    }

    public String format(Set<String> cells) {
        StringBuilder sb = new StringBuilder();
        for (String cell : cells) {
            if (sb.length() > 0) sb.append(' ');
            sb.append(cell);
        }

        return sb.toString();
    }
}

Answer 12

Penrose-esque projection of 7-dimensional lattice (64+ points)

This is similar to the Penrose tiling (to get a Penrose tiling replace N = 7 with N = 5) and qualifies for the aperiodic bonus (40 points).

Still life (2 points): trivial because the protocells are convex, so any vertex of order 3 or more suffices. (Pick all of its faces if it is order 3, or any 4 of them otherwise).

Short-period oscillators (15 points):

This tiling is rich in oscillators. The smallest period for which I've only found one oscillator is 11, and the smallest period for which I've found none is 13.

Long-period oscillator (7 points):

I deliberately chose one of the variants of this tiling which has rotational symmetry, and that turned out to be useful for the long-period oscillator. It does one-seventh of a rotation around the central point every 28 generations, making it a p196.

The code uses the framework which I posted in earlier answers together with the following tiling class:

import java.awt.geom.Point2D;
import java.util.*;

public class Penrose7Tiling implements Tiling<Penrose7Tiling.Rhomb> {
    private Map<String, Rhomb> rhombs = new HashMap<String, Rhomb>();

    private static final int N = 7;
    private double scale = 16;
    private double[] gamma;
    // Nth roots of unity.
    private Point2D.Double[] zeta;

    public Penrose7Tiling() {
        gamma = new double[N];
        zeta = new Point2D.Double[N];
        for (int i = 0; i < N; i++) {
            gamma[i] = 1.0 / N; // for global rotational symmetry
            zeta[i] = new Point2D.Double(Math.cos(2 * i * Math.PI / N), Math.sin(2 * i * Math.PI / N));
        }
    }

    private Rhomb getRhomb(int r, int s, int k_r, int k_s) {
        String key = String.format("%d,%d,%d,%d", r, s, k_r, k_s);
        Rhomb rhomb = rhombs.get(key);
        if (rhomb == null) rhombs.put(key, rhomb = new Rhomb(r, s, k_r, k_s));
        return rhomb;
    }

    private int round(double val) {
        return (int)Math.round(scale * val);
    }

    public class Rhomb {
        public int[] k;
        public int r, s;

        private int[] xs = new int[4];
        private int[] ys = new int[4];
        private Set<Rhomb> neighbours;

        public Rhomb(int r, int s, int k_r, int k_s) {
            assert 0 <= r && r < s && s < N;

            this.r = r;
            this.s = s;

            // z_0 satisfies z_0 * zeta_{r,s} + gamma_{r,s} = k_{r,s}
            Point2D.Double z_0 = solveLinear(zeta[r].x, -zeta[r].y, gamma[r] - k_r, zeta[s].x, -zeta[s].y, gamma[s] - k_s);

            // Find base lattice point.
            Point2D.Double p = new Point2D.Double();
            k = new int[N];
            for (int i = 0; i < N; i++) {
                int k_i;
                if (i == r) k_i = k_r;
                else if (i == s) k_i = k_s;
                else k_i = (int)Math.ceil(z_0.x * zeta[i].x - z_0.y * zeta[i].y + gamma[i]);

                k[i] = k_i;
                p.x += zeta[i].x * (k_i + gamma[i]);
                p.y += zeta[i].y * (k_i + gamma[i]);
            }

            xs[0] = round(p.x);
            ys[0] = round(p.y);
            xs[1] = round(p.x + zeta[r].x);
            ys[1] = round(p.y + zeta[r].y);
            xs[2] = round(p.x + zeta[r].x + zeta[s].x);
            ys[2] = round(p.y + zeta[r].y + zeta[s].y);
            xs[3] = round(p.x + zeta[s].x);
            ys[3] = round(p.y + zeta[s].y);
        }

        public Set<Rhomb> neighbours() {
            if (neighbours == null) {
                neighbours = new HashSet<Rhomb>();

                // There are quite a few candidates, but we have to check them...
                for (int nr = 0; nr < N - 1; nr++) {
                    for (int ns = nr + 1; ns < N; ns++) {
                        if (nr == r && ns == s) continue; // Can't happen.
                        for (int nk_r = k[nr] - 1; nk_r <= k[nr]; nk_r++) {
                            for (int nk_s = k[ns] - 1; nk_s <= k[ns]; nk_s++) {
                                Rhomb candidate = getRhomb(nr, ns, nk_r, nk_s);

                                // Our lattice points are (k) plus one or both of vec[r] and vec[s]
                                // where vec[0] = (1, 0, 0, ...), vec[1] = (0, 1, 0, ...), etc.
                                // Candidate has a similar set of 4 lattice points. Is there any agreement?
                                boolean isNeighbour = true;
                                for (int i = 0; i < N; i++) {
                                    int myMin = k[i], myMax = k[i] + ((i == r || i == s) ? 1 : 0);
                                    int cMin = candidate.k[i], cMax = candidate.k[i] + ((i == nr || i == ns) ? 1 : 0);
                                    if (myMin > cMax || cMin > myMax) isNeighbour = false;
                                }
                                if (isNeighbour) neighbours.add(candidate);
                            }
                        }
                    }
                }
            }

            return neighbours;
        }

        @Override
        public String toString() {
            return String.format("%d,%d,%d,%d", r, s, k[r], k[s]);
        }
    }

    // Solves ax + by + c = dx + ey + f = 0
    private Point2D.Double solveLinear(double a, double b, double c, double d, double e, double f) {
        double det = a*e - b*d;
        double x = (b*f - c*e) / det;
        double y = (c*d - a*f) / det;
        return new Point2D.Double(x, y);
    }

    public Set<Rhomb> neighbours(Rhomb cell) {
        return cell.neighbours();
    }

    public int[][] bounds(Rhomb cell) {
        // Will be modified. Copy-clone for safety.
        return new int[][]{ cell.xs.clone(), cell.ys.clone() };
    }

    public Rhomb initialCell() {
        return getRhomb(0, 1, 0, 0);
    }

    public boolean isInterestingOscillationPeriod(int period) {
        return period == 11 || period == 13 || (period > 14 && period != 26);
    }

    public Set<Rhomb> parseCells(String[] data) {
        Set<Rhomb> rv = new HashSet<Rhomb>();
        for (String key : data) {
            String[] parts = key.split(",");
            int r = Integer.parseInt(parts[0]);
            int s = Integer.parseInt(parts[1]);
            int k_r = Integer.parseInt(parts[2]);
            int k_s = Integer.parseInt(parts[3]);
            rv.add(getRhomb(r, s, k_r, k_s));
        }
        return rv;
    }

    public String format(Set<Rhomb> cells) {
        StringBuilder sb = new StringBuilder();
        for (Rhomb cell : cells) {
            if (sb.length() > 0) sb.append(' ');
            sb.append(cell);
        }

        return sb.toString();
    }
}

Answer 13

java, points-currently 11

This is the new and improved version of the one above, except without a fatal flaw!

try it here, now with random button! (press several times to get more fill) Also included speed button.

First one, period 4 oscillator, 3 points

Next, 2 3 period 2 oscillators - 3 points

2 more 2 period oscillators, courtesy of Martin Büttner (oooohhhhhhh... color)

I made a program to run it randomly and continuously, looking for oscillations. It found this one. period 5 +3 points

And another period 5, found by the randomizer.

And of course, a still life (as an example, there are many) 2 points

Code- Main class

import java.awt.Dimension;
import java.awt.GridBagConstraints;
import java.awt.GridBagLayout;
import java.awt.Point;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.util.ArrayList;

import javax.swing.JApplet;
import javax.swing.JButton;
import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JPanel;
import javax.swing.JTextField;
import javax.swing.Timer;
import javax.swing.event.DocumentEvent;
import javax.swing.event.DocumentListener;

public class Main{
    public static void main(String[] args) {
        new Main();
    }

    Canvas canvas = new Canvas();
    JFrame frame = new JFrame();
    Timer timer;
    ShapeInfo info;
    int[][][] history;
    public Main() {
        JPanel panel = new JPanel();
        panel.setMinimumSize(new Dimension(500,500));
        panel.setLayout(new GridBagLayout());

        frame.setMinimumSize(new Dimension(500,500));
        frame.getContentPane().add(panel);
        frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

        //frame.setResizable(false);
        canvas.setMinimumSize(new Dimension(200,200));
        GridBagConstraints c = new GridBagConstraints();
        c.gridx = 0;
        c.gridy = 2;
        c.weightx = 1;
        c.weighty = 1;
        c.gridwidth = 3;
        c.fill = GridBagConstraints.BOTH;
        panel.add(canvas,c);

        JButton startButton = new JButton();
        startButton.setText("click to start");
        startButton.setMaximumSize(new Dimension(100,50));
        GridBagConstraints g = new GridBagConstraints();
        g.gridx =0;
        g.gridy = 0;
        g.weightx = 1;
        panel.add(startButton,g);

        JButton restartButton = new JButton();
        restartButton.setText("revert");
        GridBagConstraints b = new GridBagConstraints();
        b.gridx = 0;
        b.gridy = 9;
        panel.add(restartButton,b);

        JButton clearButton = new JButton();
        clearButton.setText("Clear");
        GridBagConstraints grid = new GridBagConstraints();
        grid.gridx = 1;
        grid.gridy = 0;
        panel.add(clearButton,grid);

        JButton randomButton = new JButton();
        randomButton.setText("fill randomly");
        GridBagConstraints rt = new GridBagConstraints();
        rt.gridx = 2;
        rt.gridy = 0;
        panel.add(randomButton,rt);

        JLabel speedLabel = new JLabel();
        speedLabel.setText("speed");
        GridBagConstraints rt2 = new GridBagConstraints();
        rt2.gridx = 3;
        rt2.gridy = 0;
        panel.add(speedLabel,rt2);

        final JTextField speed = new JTextField();
        speed.setText("300");
        GridBagConstraints rt21 = new GridBagConstraints();
        rt21.gridx = 4;
        rt21.gridy = 0;
        panel.add(speed,rt21);

        speed.getDocument().addDocumentListener(new DocumentListener(){

            @Override
            public void changedUpdate(DocumentEvent arg0) {
                doSomething();

            }
            @Override
            public void insertUpdate(DocumentEvent arg0) {
                doSomething();

            }
            @Override
            public void removeUpdate(DocumentEvent arg0) {
                doSomething();

            }   
            public void doSomething(){
                try{int s = Integer.valueOf(speed.getText());
                timer.setDelay(s);}
                catch(Exception e){}
            }
        });

        randomButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) { 
                for(int i = 0; i< canvas.squaresHigh*canvas.squaresWide/2;i++){
                    double rx = Math.random();
                    double ry = Math.random();
                    int position = (int) Math.floor(Math.random() * 13);
                    int x = (int)(rx * canvas.squaresWide);
                    int y = (int)(ry * canvas.squaresHigh);
                    if(x!=0&&x!=canvas.squaresWide-1&&y!=0&&y!=canvas.squaresHigh-1){
                        info.allShapes[x][y][position] = 1;
                    }
                }
                history = cloneArray(info.allShapes);
                canvas.draw(info.allShapes);
            }
        });

        clearButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                info = new ShapeInfo(canvas.squaresWide,canvas.squaresHigh);
                restart();
            }
        });

        final JTextField scaleFactor = new JTextField();
        scaleFactor.setText("5");
        GridBagConstraints gh = new GridBagConstraints();
        gh.gridx  = 0;
        gh.gridy = 1;
        panel.add(scaleFactor,gh);
        scaleFactor.getDocument().addDocumentListener(new DocumentListener(){

            @Override
            public void changedUpdate(DocumentEvent arg0) {
                doSomething();
            }

            @Override
            public void insertUpdate(DocumentEvent arg0) {
                doSomething();
            }

            @Override
            public void removeUpdate(DocumentEvent arg0) {
                doSomething();
            }
            public void doSomething(){
                try{
                canvas.size = Integer.valueOf(scaleFactor.getText());
                canvas.draw(info.allShapes);
                }
                catch(Exception e){}
            }

        });
        timer = new Timer(300, listener);
        frame.pack();
        frame.setVisible(true);
        info = new ShapeInfo(canvas.squaresWide, canvas.squaresHigh);
        info.width = canvas.squaresWide;
        info.height = canvas.squaresHigh;
        history = cloneArray(info.allShapes);
        //history[8][11][1] = 1;
        canvas.draw(info.allShapes);
        restartButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                if(timer.isRunning() == true){
                    info.allShapes = cloneArray(history);
                    restart();
                }
            }
        });
        canvas.addMouseListener(new MouseListener(){
            @Override
            public void mouseClicked(MouseEvent e) {
                int x = e.getLocationOnScreen().x - canvas.getLocationOnScreen().x;
                int y = e.getLocationOnScreen().y - canvas.getLocationOnScreen().y;
                Point location = new Point(x,y);
                for(PolygonInfo p:canvas.polygons){
                    if(p.polygon.contains(location)){
                        if(info.allShapes[p.x][p.y][p.position] == 1){
                            info.allShapes[p.x][p.y][p.position] = 0;
                        }
                        else{
                            info.allShapes[p.x][p.y][p.position] = 1;
                        }
                    }
                }
                canvas.draw(info.allShapes);
                history = cloneArray(info.allShapes);
            }
            @Override
            public void mouseEntered(MouseEvent arg0) {
            }
            @Override
            public void mouseExited(MouseEvent arg0) {
            }
            @Override
            public void mousePressed(MouseEvent arg0) { 
            }
            @Override
            public void mouseReleased(MouseEvent arg0) {    
            }
        });
        startButton.addActionListener(new ActionListener(){
            @Override
            public void actionPerformed(ActionEvent arg0) {
                timer.start();
            }
        });
    }
    public int[][][] cloneArray(int[][][] array){
        int[][][] newArray = new int[array.length][array[0].length][array[0][0].length];
        for(int x = 0;x<array.length;x++){
            int[][] subArray = array[x];
            for(int y = 0; y < subArray.length;y++){
                int subSubArray[] = subArray[y];
                newArray[x][y] = subSubArray.clone();
            }
        }
        return newArray;
    }
    public void restart(){
        timer.stop();
        canvas.draw(info.allShapes);
    }
    public void setUp(){
        int[] boxes = new int[]{2,3,4,6,7,8};
        for(int box:boxes){
            info.allShapes[8][12][box-1] = 1;
            info.allShapes[9][13][box-1] = 1;
            info.allShapes[8][14][box-1] = 1;
            info.allShapes[9][15][box-1] = 1;
        }
    }
    public void update() {
        ArrayList<Coordinate> dieList = new ArrayList<Coordinate>();
        ArrayList<Coordinate> appearList = new ArrayList<Coordinate>();
        for (int x = 0; x < canvas.squaresWide; x++) {
            for (int y = 0; y < canvas.squaresHigh; y++) {
                for(int position = 0;position <13;position++){
                    int alive = info.allShapes[x][y][position];
                    int touching = info.shapesTouching(x, y, position);
                    if(touching!=0){
                    }
                    if(alive == 1){
                        if(touching < 2 || touching > 3){
                            //cell dies
                            dieList.add(new Coordinate(x,y,position));
                        }
                    }
                    else{
                        if(touching == 3){
                            //cell appears
                            appearList.add(new Coordinate(x,y,position));
                        }
                    }
                }
            }
        }
        for(Coordinate die:dieList){
            info.allShapes[die.x][die.y][die.position] = 0;
        }
        for(Coordinate live:appearList){
            info.allShapes[live.x][live.y][live.position] = 1;
        }
    }
    boolean firstDraw = true;
    int ticks = 0;
    ActionListener listener = new ActionListener() {
        @Override
        public void actionPerformed(ActionEvent arg0) {
            canvas.draw(info.allShapes);
            if(ticks !=0){
            update();
            }
            ticks++;
        }
    };
}

Canvas -

import java.awt.Color;
import java.awt.Graphics;
import java.awt.Polygon;
import java.util.ArrayList;

import javax.swing.JPanel;

public class Canvas extends JPanel {
    private static final long serialVersionUID = 1L;

    public int squaresWide = 30;
    public int squaresHigh = 30;
    public int size = 6;
    ArrayList<PolygonInfo> polygons = new ArrayList<PolygonInfo>();
    boolean drawTessalationOnly = true;
    private int[][][] shapes;

    public void draw(int[][][] shapes2) {
        shapes = shapes2;
        drawTessalationOnly = false;
        this.repaint();
    }

    @Override
    protected void paintComponent(Graphics g) {
        //System.out.println("drawing");
        polygons.clear();
        super.paintComponent(g);
        g.setColor(Color.black);
        // draw tessellation
        for (int x = 0; x < squaresWide; x++) {
            for (int y = 0; y < squaresHigh; y++) {
                for (int position = 0; position < 13; position++) {
                    // System.out.println("position = " + position);
                    Polygon p = new Polygon();
                    int points = 0;
                    int[] xc = new int[] {};
                    int[] yc = new int[] {};
                    if (position == 0) {
                        xc = new int[] {-2,0,2,0};
                        yc = new int[] {0,-2,0,2};
                        points = 4;
                    }
                    if (position == 1) {
                        xc = new int[] {2,4,4,1};
                        yc = new int[] {0,0,2,1};
                        points = 4;
                    }
                    if (position == 2) {
                        xc = new int[] {4,6,7,4};
                        yc = new int[] {0,0,1,2};
                        points = 4;
                    }
                    if (position == 3) {
                        xc = new int[] {1,2,0,0};
                        yc = new int[] {1,4,4,2};
                        points = 4;
                    }
                    if (position == 4) {
                        xc = new int[] {1,4,4,2};
                        yc = new int[] {1,2,4,4};
                        points = 4;
                    }
                    if (position == 5) {
                        xc = new int[] {7,6,4,4};
                        yc = new int[] {1,4,4,2};
                        points = 4;
                    }
                    if (position == 6) {
                        xc = new int[] {7,8,8,6};
                        yc = new int[] {1,2,4,4};
                        points = 4;
                    }
                    if (position == 7) {
                        xc = new int[] {0,2,1,0};
                        yc = new int[] {4,4,7,6};
                        points = 4;
                    }
                    if (position == 8) {
                        xc = new int[] {1,2,4,4};
                        yc = new int[] {7,4,4,6};
                        points = 4;
                    }
                    if (position == 9) {
                        xc = new int[] {7,6,4,4};
                        yc = new int[] {7,4,4,6};
                        points = 4;
                    }
                    if (position == 10) {
                        xc = new int[] {8,6,7,8};
                        yc = new int[] {4,4,7,6};
                        points = 4;
                    }
                    if (position == 11) {
                        xc = new int[] {4,4,2,1};
                        yc = new int[] {6,8,8,7};
                        points = 4;
                    }
                    if (position == 12) {
                        xc = new int[] {4,4,6,7};
                        yc = new int[] {6,8,8,7};
                        points = 4;
                    }
                    int[] finalX = new int[xc.length];
                    int[] finalY = new int[yc.length];
                    for (int i = 0; i < xc.length; i++) {
                        int xCoord = xc[i];
                        xCoord = (xCoord + (8 * x)) * size;
                        finalX[i] = xCoord;
                    }
                    for (int i = 0; i < yc.length; i++) {
                        int yCoord = yc[i];
                        yCoord = (yCoord + (8 * y)) * size;
                        finalY[i] = yCoord;
                    }
                    p.xpoints = finalX;
                    p.ypoints = finalY;
                    p.npoints = points;
                    polygons.add(new PolygonInfo(p,x,y,position));
                    // for(int i = 0;i<p.npoints;i++){
                    // / System.out.println("(" + p.xpoints[i] + "," +
                    // p.ypoints[i] + ")");
                    // }
                    if (drawTessalationOnly == false) {
                        if (shapes[x][y][position] == 1) {
                            g.setColor(Color.black);
                            g.fillPolygon(p);
                        } else {
                            g.setColor(Color.black);
                            g.drawPolygon(p);
                        }
                    } else {
                        g.drawPolygon(p);
                    }
                }

            }
        }
    }
}

ShapeInfo -

public class ShapeInfo {
    int[][][] allShapes; // first 2 dimensions are coordinates of large square,
                            // last is boolean - if shaded
    int width = 30;
    int height = 30;

    public ShapeInfo(int width, int height) {
        allShapes = new int[width][height][13];
        for (int[][] i : allShapes) {
            for (int[] h : i) {
                for (int g : h) {
                    g = 0;
                }
            }
        }
    }

    public int shapesTouching(int x, int y, int position) {
        int t = 0;
        if (x > 0 && y > 0 && x < width - 1 && y < height - 1) {
            int[] inShape = new int[]{};
            int[] rightOfShape = new int[]{};
            int[] aboveShape = new int[]{};
            int[] leftOfShape = new int[]{};
            int[] belowShape = new int[]{};
            int[] aboveRightOfShape = new int[]{};
            int[] aboveLeftOfShape = new int[]{};
            int[] belowRightOfShape = new int[]{};
            int[] belowLeftOfShape = new int[]{};
            if (position == 0) {
                inShape = new int[]{1,3,4};
                aboveShape = new int[]{7,8,11};
                leftOfShape = new int[]{2,5,6};
                aboveLeftOfShape = new int[]{10,12,9};
            }
            if (position == 1) {
                inShape = new int[]{0,3,4,5,2};
                aboveShape = new int[]{11,12};
            }
            if (position == 2) {
                inShape = new int[]{1,4,5,6};
                rightOfShape = new int[]{0};
                aboveShape = new int[]{12,11};
            }
            if (position == 3) {
                inShape = new int[]{0,1,4,8,7};
                leftOfShape = new int[]{6,10};
            }
            if (position == 4) {
                inShape = new int[]{0,1,3,2,7,5,8,9};
            }
            if (position == 5) {
                inShape = new int[]{2,6,1,10,4,9,8};
                rightOfShape = new int[]{0};
            }
            if (position == 6) {
                inShape = new int[]{2,5,9,10};
                rightOfShape = new int[]{0,3,7};
            }
            if (position == 7) {
                inShape = new int[]{3,4,8,11};
                leftOfShape =new int[]{6,10};
                belowShape = new int[]{0};
            }
            if (position == 8) {
                inShape = new int[]{5,4,9,3,12,7,11};
                belowShape = new int[]{0};
            }
            if (position == 9) {
                inShape = new int[]{4,5,8,6,11,12,10};
                belowRightOfShape = new int[]{0};
            }
            if (position == 10) {
                inShape = new int[]{6,5,9,12};
                rightOfShape = new int[]{3,7};
                belowRightOfShape = new int[]{0};
            }
            if (position == 11) {
                inShape = new int[]{7,8,9,12};
                belowShape = new int[]{0,1,2};
            }
            if (position == 12) {
                inShape = new int[]{11,8,9,10};
                belowShape = new int[]{1,2};
                belowRightOfShape = new int[]{0};
            }
            for(int a:inShape){
                if(allShapes[x][y][a] == 1){t++;}
            }
            for(int a:rightOfShape){
                if(allShapes[x+1][y][a] == 1){t++;}
            }
            for(int a:leftOfShape){
                if(allShapes[x-1][y][a] == 1){t++;}
            }
            for(int a:aboveShape){
                if(allShapes[x][y-1][a] == 1){t++;}
            }
            for(int a:belowShape){
                if(allShapes[x][y+1][a] == 1){t++;}
            }
            for(int a:aboveRightOfShape){
                if(allShapes[x+1][y-1][a] == 1){t++;}
            }
            for(int a:aboveLeftOfShape){
                if(allShapes[x-1][y-1][a] == 1){t++;}
            }
            for(int a:belowRightOfShape){
                if(allShapes[x+1][y+1][a] == 1){t++;}
            }
            for(int a:belowLeftOfShape){
                if(allShapes[x-1][y+1][a] == 1){t++;}
            }
        }
        return t;
    }
}

Coordinate -

public class Coordinate {
    int x;
    int y;
    int position;
    public Coordinate(int X,int Y, int Position){
        x=X;
        y=Y;
        position = Position;
    }
}

PolygonInfo

import java.awt.Polygon;

public class PolygonInfo {
    public Polygon polygon;
    public int x;
    public int y;
    public int position;
    public PolygonInfo(Polygon p,int X,int Y,int Position){
        x = X;
        y = Y;
        polygon = p;
        position = Position;
    }
}

If anyone finds any, they will be mentioned. (Which reminds me: my brother found the first 2 oscillators)

Answer 14

Javascript, HexagonSplit

Disclaimer: Its pretty slow due to lots of dom manipulation and probably needs a bugfix for the x-axis to not wrap-around.

Fiddle

http://jsfiddle.net/16bhsr52/9/

Fiddle now allows to toggle active cells.

Still Live

Oscillator

Spaceship (2 phases, two variants)

Spacehip (4 phases)

Javascript

//--  Prepare  --
var topX = 0;
var topY = 0;
var sizeX = 40;
var sizeY = 10;
var patternSizeX = 17;
var patternSizeY = 43;
var patternElements = 3;
var neighbourTopLeft = -(sizeX + 1) * patternElements;
var neighbourTop = -(sizeX) * patternElements;
var neighbourTopRight = -(sizeX - 1) * patternElements;
var neighbourLeft = -patternElements;
var neighbourRight = +patternElements;
var neighbourBottomLeft = +(sizeX - 1) * patternElements;
var neighbourBottom = +(sizeX) * patternElements;
var neighbourBottomRight = +(sizeX + 1) * patternElements;
var patternNeighbours = [
    [neighbourTopLeft + 2, neighbourTop + 2, neighbourTopRight + 2, neighbourLeft, neighbourLeft + 1, 1, neighbourRight],
    [neighbourLeft + 1, 0, 2, neighbourRight, neighbourRight + 1, neighbourRight + 2],
    [neighbourLeft + 1, neighbourLeft + 2, 1, neighbourRight + 2, neighbourBottomLeft, neighbourBottom, neighbourBottomRight]
];

for (i = 0; i < sizeX; i++) {
    for (j = 0; j < sizeY; j++) {
        var tileId = (j * sizeX + i) * patternElements;
        $("body").append('<div id="t' + (tileId) + '" class="shapeDown" style="left:' + topX + patternSizeX * i + 'px;top:' + topY + patternSizeY * j + 'px;">');
        $("body").append('<div id="t' + (tileId + 1) + '" class="shapeHexagon" style="left:' + (8 + topX + patternSizeX * i) + 'px;top:' + (17 + topY + patternSizeY * j) + 'px;">');
        $("body").append('<div id="t' + (tileId + 2) + '" class="shapeUp" style="left:' + topX + patternSizeX * i + 'px;top:' + (34 + topY + patternSizeY * j) + 'px;">');
    }
}

//--  Populate  --
for (i = 0; i < (patternElements * sizeX * sizeY) / 5; i++) {
    $("#t" + Math.floor((Math.random() * (patternElements * sizeX * sizeY)))).addClass("shapeAlive");
};

//--  Animate  --
setInterval(progress, 1000);

function progress() {
    var dying = [];
    var rising = [];

    for (i = 0; i < sizeX; i++) {
        for (j = 0; j < sizeY; j++) {
            var tileBaseId = (j * sizeX + i) * patternElements;
            for (k = 0; k < patternElements; k++) {
                var tileSelect = "#t" + (tileBaseId + k);
                var alive = $(tileSelect).filter(".shapeAlive").length;
                var nbSelect = $.map(patternNeighbours[k], function (n, i) {
                    return ("#t" + (tileBaseId + n));
                }).join();
                var count = $(nbSelect).filter(".shapeAlive").length;
                if (alive && (count < 2 || count > 3)) {
                    dying.push(tileSelect);
                };
                if (!alive && count == 3) {
                    rising.push(tileSelect);
                };
            }
        }
    }

    $(dying.join()).removeClass("shapeAlive");
    $(rising.join()).addClass("shapeAlive");
};

CSS

.shapeHexagon {
    background-color: black;
    height: 8px;
    width: 16px;
    position: absolute;
}
.shapeUp {
    background-color: black;
    height: 8px;
    width: 16px;
    position: absolute;
}
.shapeUp:after, .shapeHexagon:before {
    content:"";
    position: absolute;
    top: -8px;
    left: 0px;
    width: 0;
    height: 0;
    border-style: solid;
    border-color: transparent transparent black;
    border-width: 0px 8px 8px 8px;
}
.shapeAlive.shapeUp {
    background-color: green;
}
.shapeAlive.shapeUp:after {
    border-color: transparent transparent green;
}
.shapeDown {
    background-color: black;
    height: 8px;
    width: 16px;
    position: absolute;
}
.shapeDown:after, .shapeHexagon:after {
    content:"";
    position: absolute;
    top: 8px;
    left: 0px;
    width: 0;
    height: 0;
    border-style: solid;
    border-color: black transparent transparent transparent;
    border-width: 8px 8px 0 8px;
}
.shapeAlive.shapeUp:after, .shapeAlive.shapeHexagon:before {
    border-color: transparent transparent green;
}
.shapeAlive.shapeDown, .shapeAlive.shapeHexagon {
    background-color: green;
}
.shapeAlive.shapeDown:after, .shapeAlive.shapeHexagon:after {
    border-color: green transparent transparent transparent;
}

Answer 15

"Hex Medley 3" (24+ points*)

Inspired by the floret pentagonal tiling: a block of 7 hexagons tiles the plane, and we can chop the hexagons up in a lot of different ways. As the name suggests, this is the third such variation I tried, but it's worth posting because it's the first tiling to claim the 7 points for a p30+ oscillator.

The tiling is:

Since the protocells are convex, any order-3 vertex gives a still-life (2 points).

I have found five small-period oscillators (15 points): periods 2, 3, 4, 6, 12.

And the pièce de résistance: a p48 oscillator (7 points) which rotates by 60 degrees every 8 generations:

* Given the nature of this tiling I could pick a single hex which is divided into rhombi and rotate it 60 degrees. This would make the tiling aperiodic without technically breaking any rules, and wouldn't break any of the oscillators either. But I don't think it's in the spirit of the question, so I won't try to claim those 40 points.

The code relies on a lot of code I've posted in other answers; the unique part is

public class HexMedley3 extends AbstractLattice {
    public HexMedley3() {
        super(35, -12, 28, 24, new int[][] {
                {0, 0, 7},
                {0, 7, 7},
                {0, 7, 0},
                {0, 0, -7},
                {0, -7, -7},
                {0, -7, 0},

                {0, 0, 7, 7},
                {7, 7, 14, 14},
                {7, 14, 7, 0},

                {7, 14, 21, 14},
                {14, 21, 21, 14},
                {14, 14, 7, 7},

                {7, 14, 14, 7},
                {7, 14, 7, 0},
                {7, 0, 0, 7},

                {0, 0, -7, -7},
                {-7, -7, -14, -14},
                {-7, -14, -7, 0},

                {-7, -14, -21, -14},
                {-14, -21, -21, -14},
                {-14, -14, -7, -7},

                {-7, -14, -14, -7},
                {-7, -14, -7, 0},
                {-7, 0, 0, -7},

            }, new int[][] {
                {0, 8, 4},
                {0, 4, -4},
                {0, -4, -8},
                {0, -8, -4},
                {0, -4, 4},
                {0, 4, 8},
                {8, 16, 20, 12},
                {12, 20, 16, 8},
                {12, 8, 4, 8},
                {4, 8, 4, 0},
                {0, 4, -4, -8},
                {0, -8, -4, 4},
                {-4, -8, -16, -12},
                {-12, -16, -20, -16},
                {-12, -16, -8, -4},

                {-8, -16, -20, -12},
                {-12, -20, -16, -8},
                {-12, -8, -4, -8},
                {-4, -8, -4, 0},
                {0, -4, 4, 8},
                {0, 8, 4, -4},
                {4, 8, 16, 12},
                {12, 16, 20, 16},
                {12, 16, 8, 4},
            });
    }

    @Override
    public boolean isInterestingOscillationPeriod(int period) {
        return period != 2 && period != 4;
    }
}

Answer 16

Rectangles of width 2^row in Python 3, +2

The shape of this grid is as follows:

 ______________
[______________]
[______][______]
[__][__][__][__]
[][][][][][][][]

Coincidentally, each cell in this grid has 8 neighbors, just like the original square tiling of the Game of Life.

Unfortunately, this tiling has the terrible property that each cell only has two north neighbors. That means a pattern can never propagate southward, including southeast or southwest. This property leads to a situation that makes oscillators rather unlikely, although one might exist of the sort that has walls on two sides and blinking cells in the middle.

It also seems to have the property (I'm not 100% sure yet) that no pattern can grow while moving north. A row will never grow to a wider maximum extent number of cells than the row below it. I think that means no gliders or more complicated forms.

That leaves us with a measly +2 bonus for a wide variety of still lifes, of which these are only a small sample:

AA__
_BC_

AABB
_CD_

AA__BB
_CXXD_ <-- XX can be any multiple of 2 wide

____YYYY____
__AA____BB__
___CXXXXD___ <-- XX can be any multiple of 4 wide

____YYYYOOOO <-- OOOO can continue to the right and could be the bottom of a stack of this pattern
__AA____BB__
___CXXXX____ <-- XX can be any multiple of 4 wide

OOOOYYYYOOOO <-- same stackability as above
__AA____BB__
____XXXX____ <-- XX can be any multiple of 4 wide

Here is the code, which when run will draw an 8-row grid (1 cell in the top row, 128 cells in the bottom row). Any key will advance one step, except r will randomize the board and q will exit the program.

#!/usr/bin/env python3

import random
import readchar

class board:
  def __init__(self, rows = 8):
    if rows>10:
      raise ValueError("Too many rows!")
    self.rows = rows
    self.cells = [[cell() for c in range(int(2**(r)))] for r in range(rows)]
  def __str__(self):
    out = []
    for r,row in enumerate(self.cells):
      out.append(''.join([str(row[c])*(2**(self.rows-r-1)) for c in range(len(row))]))
    return "\n".join(out)
  def randomize(self):
    for row in self.cells:
      for c,cel in enumerate(row):
        row[c].state = random.choice([True,False])
  def state_at(self,r,c):
    if r==None or c==None:
      raise TypeError()
    if r<0 or c<0:
      return False
    if r>=self.rows:
      return False
    if c>=len(self.cells[r]):
      return False
    return self.cells[r][c].state
  def tick(self):
    new_cells = [[cell() for c in range(int(2**(r)))] for r in range(self.rows)]
    for r,row in enumerate(self.cells):
      for c,cel in enumerate(row):
        # print(f"cell {r} {c}")
        cur = cel.state
        # print(cur)
        neighbors = 0
        # same row, left and right
        neighbors += self.state_at(r,c-1)
        neighbors += self.state_at(r,c+1)
        # straight up
        neighbors += self.state_at(r-1,int(c/2))
        # straight down
        neighbors += self.state_at(r+1,c*2)
        neighbors += self.state_at(r+1,c*2+1)
        # down left
        neighbors += self.state_at(r+1,c*2-1)
        # down right
        neighbors += self.state_at(r+1,c*2+2)
        if c%2==0:
          # up left
          neighbors += self.state_at(r-1,int(c/2)-1)
        else:
          # up right
          neighbors += self.state_at(r-1,int(c/2)+1)
        # print(neighbors)
        if cur:
          if neighbors<2 or neighbors>3:
            # print("turn off")
            new_cells[r][c].state = False
          else:
            new_cells[r][c].state = True
          continue
        if neighbors==3:
          # print("turn on")
          new_cells[r][c].state = True
          continue
        new_cells[r][c].state = False
        continue
    self.cells = new_cells

class cell:
  def __init__(self, state = False):
    self.state = state
  def __str__(self):
    return self.state and "X" or "_"

b = board(8)
b.randomize()
print(b)
while(1):
  i = readchar.readchar()
  if i=='q':
    break
  if i=='r':
    b.randomize()
  b.tick()
  print()
  print(b)

PS: This grid is the equivalent of regular in a particularly shaped non-Euclidean space :)