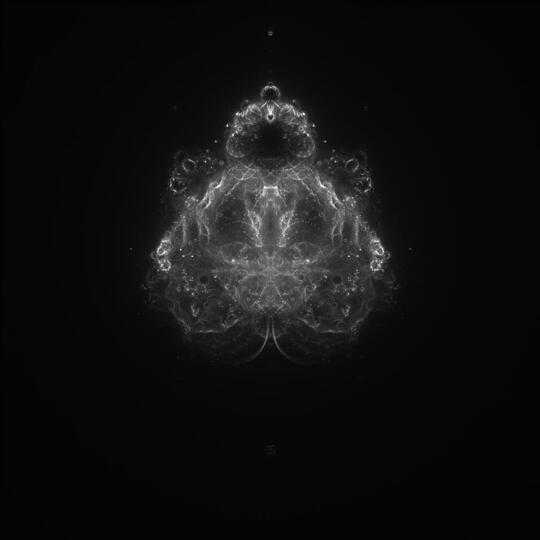
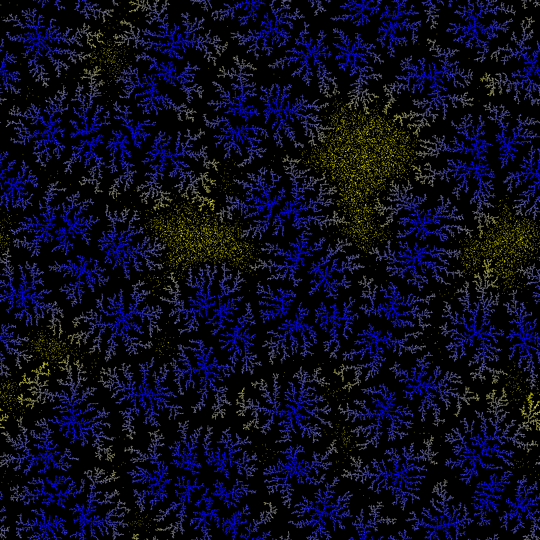
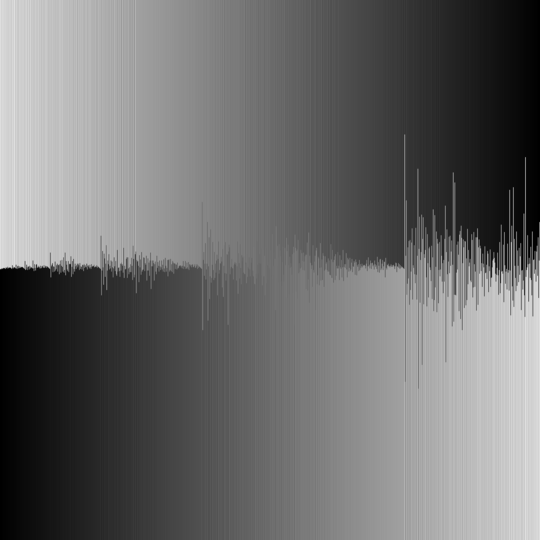
OK, this one gave me a hard time. I think it's pretty nice though, even if the results are not so arty as some others. That's the deal with randomness. Maybe some intermediate images look better, but I really wanted to have a fully working algorithm with voronoi diagrams.

Edit:

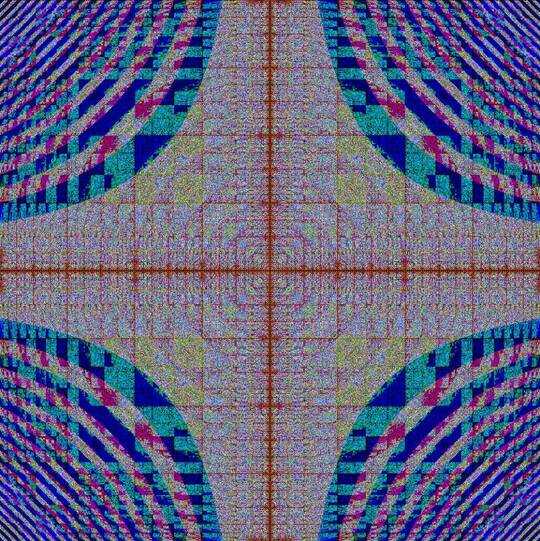
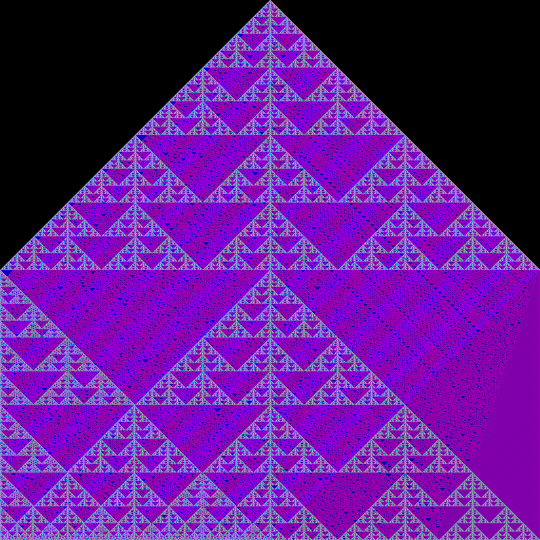
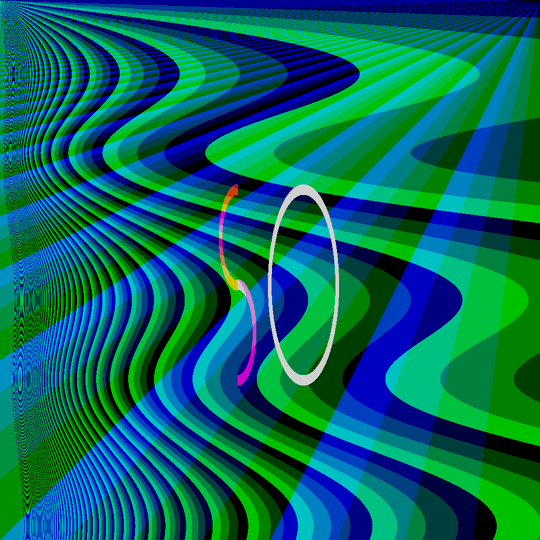
This is one example of the final algorithm. The image is basically the superposition of three voronoi diagram, one for each color component (red, green, blue).
Code
ungolfed, commented version at the end
unsigned short red_fn(int i, int j){
int t[64],k=0,l,e,d=2e7;srand(time(0));while(k<64){t[k]=rand()%DIM;if((e=_sq(i-t[k])+_sq(j-t[42&k++]))<d)d=e,l=k;}return t[l];
}
unsigned short green_fn(int i, int j){
static int t[64];int k=0,l,e,d=2e7;while(k<64){if(!t[k])t[k]=rand()%DIM;if((e=_sq(i-t[k])+_sq(j-t[42&k++]))<d)d=e,l=k;}return t[l];
}
unsigned short blue_fn(int i, int j){
static int t[64];int k=0,l,e,d=2e7;while(k<64){if(!t[k])t[k]=rand()%DIM;if((e=_sq(i-t[k])+_sq(j-t[42&k++]))<d)d=e,l=k;}return t[l];
}
It took me a lot of efforts, so I feel like sharing the results at different stages, and there are nice (incorrect) ones to show.
First step: have some points placed randomly, with x=y

I have converted it to jpeg because the original png was too heavy for upload (>2MB), I bet that's way more than 50 shades of grey!
Second: have a better y coordinate
I couldn't afford to have another table of coordinates randomly generated for the y axis, so I needed a simple way to get " random " ones in as few characters as possible. I went for using the x coordinate of another point in the table, by doing a bitwise AND on the index of the point.

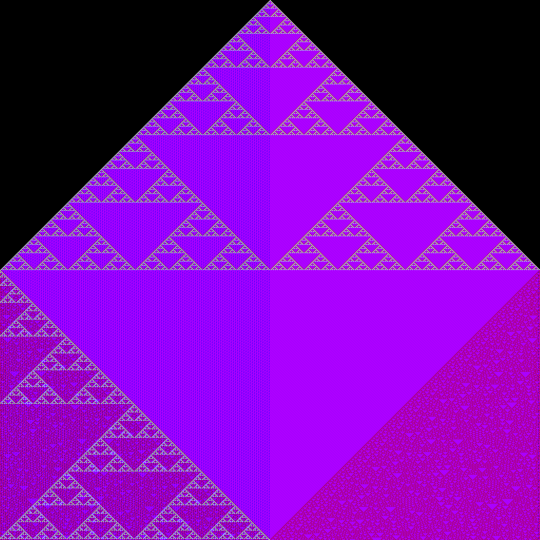
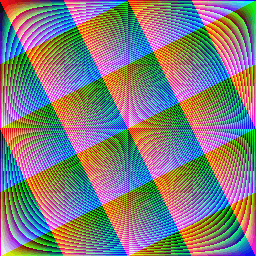
3rd: I don't remember but it's getting nice
But at this time I was way over 140 chars, so I needed to golf it down quite a bit.

4th: scanlines
Just kidding, this is not wanted but kind of cool, methinks.


Still working on reducing the size of the algorithm, I am proud to present:
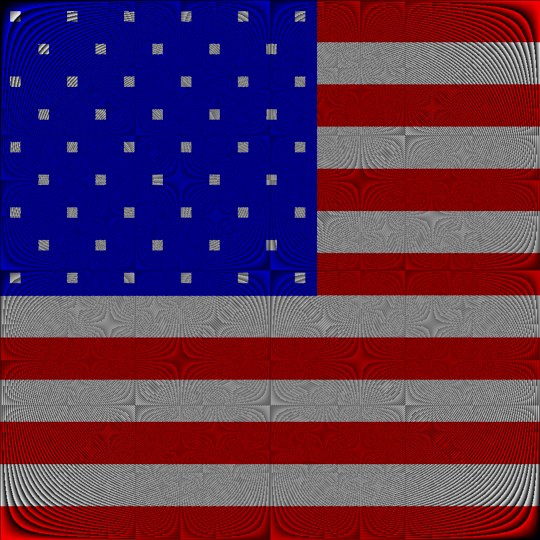
StarFox edition

Voronoi instagram

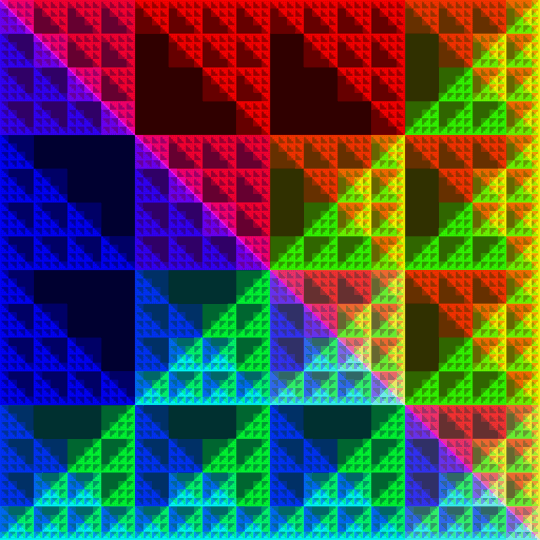
5th: increase the number of points
I have now a working piece of code, so let's go from 25 to 60 points.

That's hard to see from only one image, but the points are nearly all located in the same y range. Of course, I didn't change the bitwise operation, &42 is much better:

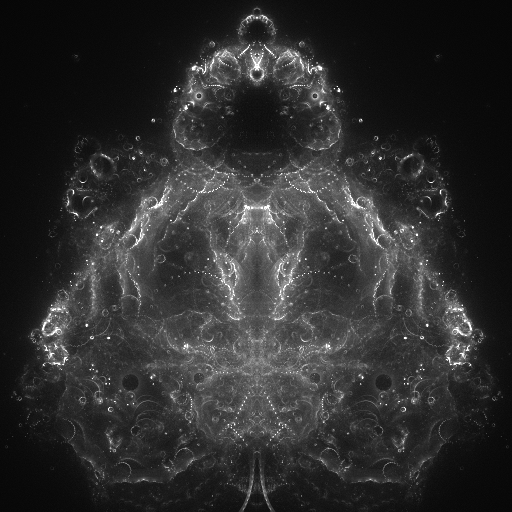
And here we are, at the same point as the very first image from this post.
Let's now explain the code for the rare ones that would be interested.
Ungolfed and explained code
unsigned short red_fn(int i, int j)
{
int t[64], // table of 64 points's x coordinate
k = 0, // used for loops
l, // retains the index of the nearest point
e, // for intermediary results
d = 2e7; // d is the minimum distance to the (i,j) pixel encoutnered so far
// it is initially set to 2e7=2'000'000 to be greater than the maximum distance 1024²
srand(time(0)); // seed for random based on time of run
// if the run overlaps two seconds, a split will be observed on the red diagram but that is
// the better compromise I found
while(k < 64) // for every point
{
t[k] = rand() % DIM; // assign it a random x coordinate in [0, 1023] range
// this is done at each call unfortunately because static keyword and srand(...)
// were mutually exclusive, lenght-wise
if (
(e= // assign the distance between pixel (i,j) and point of index k
_sq(i - t[k]) // first part of the euclidian distance
+
_sq(j - t[42 & k++]) // second part, but this is the trick to have "" random "" y coordinates
// instead of having another table to generate and look at, this uses the x coordinate of another point
// 42 is 101010 in binary, which is a better pattern to apply a & on; it doesn't use all the table
// I could have used 42^k to have a bijection k <-> 42^k but this creates a very visible pattern splitting the image at the diagonal
// this also post-increments k for the while loop
) < d // chekcs if the distance we just calculated is lower than the minimal one we knew
)
// { // if that is the case
d=e, // update the minimal distance
l=k; // retain the index of the point for this distance
// the comma ',' here is a trick to have multiple expressions in a single statement
// and therefore avoiding the curly braces for the if
// }
}
return t[l]; // finally, return the x coordinate of the nearest point
// wait, what ? well, the different areas around points need to have a
// "" random "" color too, and this does the trick without adding any variables
}
// The general idea is the same so I will only comment the differences from green_fn
unsigned short green_fn(int i, int j)
{
static int t[64]; // we don't need to bother a srand() call, so we can have these points
// static and generate their coordinates only once without adding too much characters
// in C++, objects with static storage are initialized to 0
// the table is therefore filled with 60 zeros
// see http://stackoverflow.com/a/201116/1119972
int k = 0, l, e, d = 2e7;
while(k<64)
{
if( !t[k] ) // this checks if the value at index k is equal to 0 or not
// the negation of 0 will cast to true, and any other number to false
t[k] = rand() % DIM; // assign it a random x coordinate
// the following is identical to red_fn
if((e=_sq(i-t[k])+_sq(j-t[42&k++]))<d)
d=e,l=k;
}
return t[l];
}
Thanks for reading so far.







































































































































Although I'm grateful, please don't accept the tablecloths answer. Even today there are still new votes coming in with more interesting answers bubbling their way towards the top. I encourage sorting by oldest and seeing how the answers developed over time, and having the highest voted pinned to the top will only serve to skew the voting further. – trichoplax – 2015-09-05T23:22:03.800
The tablecloths answer is my least favourite among my own answers to this question, and certainly can't compare to some of the amazing answers by others. – trichoplax – 2015-09-05T23:24:58.373
@trichoplax I agree with your first comment, but I decided to choose Manuel Kasten' s blue mandelbrot, because I've been using it as one of my backgrounds ever since he posted it. I didn't want to choose something with too few votes seeing as I tagged it as a "popularity contest" – Kyle McCormick – 2015-09-06T02:16:39.717
3Added C++ tag because the nature of the rules excludes other languages. We generally prefer language-agnostic challenges unless they have a good reason to require a specific set. – algorithmshark – 2014-08-02T04:48:32.803
@algorithmshark I was considering allowing other languages, but I'd have to require that whoever chose to do so would have to implement a nearly identical framework. I chose to make it this way to make it easier & quicker for people to work out a quick solution, rather than making it a more in-depth problem. – Kyle McCormick – 2014-08-02T05:02:02.733
@algorithmshark Edited to allow other languages. – Kyle McCormick – 2014-08-02T05:07:04.580
1@Kyle I've tried both your examples, but both give a different image to what you've shown and the second one raises a division-by-zero error that I fixed with
i|j->i&&j. Mind looking at it? – tomsmeding – 2014-08-02T06:25:00.417Just to be absolutely clear, each function body can be up to 140 characters? The three added together can be more than 140 characters? – trichoplax – 2014-08-02T10:42:09.367
2@KyleMcCormick Do you consider it cheating to define a macro in
red_fnand use it ingreen_fnandblue_fn? – Martin Ender – 2014-08-02T11:38:32.540Am I right in thinking that the function body doesn't include the enclosing braces? – trichoplax – 2014-08-02T12:20:48.490
1@MartinBüttner your macro question makes me wonder if it is acceptable to call, for example, red_fn from green_fn, with two arguments that don't necessarily relate to pixel coordinates. – trichoplax – 2014-08-02T12:24:50.660
@tomsmeding yes I believe you're right. I think I made that change (&& to |) without really thinking about it. Fixing it now. – Kyle McCormick – 2014-08-02T20:21:55.503
@MartinBüttner Feel free to do whatever you want in the space between the braces, but please do not change the function signature or write any external functions to call inside these. Also, changing to allow complex.h. – Kyle McCormick – 2014-08-02T20:34:05.317
2@githubphagocyte We'll say the opening/closing braces don't count toward your 140 char count. – Kyle McCormick – 2014-08-02T20:34:25.897
2@KyleMcCormick could you maybe add forward-declarations of the three colour functions to your framework? that would allow some funky mutual recursion. also, people porting the framework to other languages will get those capabilities for free anyway. – Martin Ender – 2014-08-02T21:34:27.243
2@MartinBüttner That sounds interesting. I'd say that isn't really in the scope of what I was looking for... but I'm curious. Updating it now. Show me what you got! – Kyle McCormick – 2014-08-02T23:03:41.343
If you are going to add forward declarations and allow mutual recursion, is there any chance you could also shorten the function names, for example
r()instead ofred_fn()? – trichoplax – 2014-08-02T23:15:37.2171Haha good call. Just a few minutes here... – Kyle McCormick – 2014-08-02T23:21:12.190
2
You guys eventually want to add it to https://commons.wikimedia.org/wiki/Category:Mathematical_art
– Martin Thoma – 2014-08-03T15:17:13.4604To the close voters calling this too broad, please try writing an answer to this first. It's surprisingly restrictive... – trichoplax – 2014-08-03T22:24:54.540
8This is my favorite thing I've seen on here in, like, ever! – David Conrad – 2014-08-04T16:25:07.140
4I love that this question feels like an old-school demo scene. – mskfisher – 2014-08-05T13:31:07.617
For those using the unsigned short (non-alternative) version of this, what are you using to display the results? Neither my version of Gimp (2.2.13) nor ImageMagick's display (6.2.8) seem to like PPM files w/ 1023 as a max. Many of these answers don't seem to work at all with the alternative version (and some produce severe palette shifts with it). – DreamWarrior – 2014-08-05T18:25:25.383
1ImageMagick should work. Didn't try display, but convert was fine. On little endian systems you might need a htons() to write the color values like so: color[0] = htons(RD(i,j)&DM1); The 16bit ppm format is big endian. Declaration of htons is in arpa/inet.h – Manuel Kasten – 2014-08-05T20:50:55.203
@ManuelKasten tried that, still didn't produce an equivalent image. However, it is required on my machine, and thus did produce more sensible images! So thanks -- don't know why I didn't think of that, though I looked up the PPM format and didn't see endian-ness listed, so maybe that's why :-). – DreamWarrior – 2014-08-06T19:04:18.037
Ugh, I didn't see it, but it was listed, haha.... Anyway, the fact remains that the answers using short still don't produce what their sample images show. For example, faubiguy's answer is just a black and white image of a gradient circle with a smooth diagonal gradient behind it. And cjfaure's answer is just a black canvas (though without the proper byte-order I get color). Oh well, I guess them's the brakes. – DreamWarrior – 2014-08-06T19:17:53.623
1I just wanted to say that these are amazing. – Matthew Flaschen – 2014-08-07T04:17:39.790
23This type of question encourages participation in code golf. I'm generally disinclined to answer a straight golf question as I'm not confident of doing well. With this type of question the byte limit makes me try a simple answer, learn golfing techniques along the way, and then use them to make more complex answers. This is like a stepping stone into answering straight golf questions. I think it could be key in bringing more people in. – trichoplax – 2014-08-07T23:43:35.860
I wonder what happens when you combine all the submissions o: – cjfaure – 2014-08-09T11:36:10.983
2Wow. 15 minutes writing an answer for this is prettier than 15 hours of hard work in MS Paint. – cjfaure – 2014-08-10T20:02:34.143
I'm curious if you considered just using GLSL and http://glsl.heroku.com or http://shadertoy.com. The cool thing is their viewable online. Just provide a template, allow 140 chars in the middle of say
– gman – 2014-08-11T00:12:43.720void main() { /* insert 140 chars here */ };1
I whipped together a website to mess around with this kind of thing. You can't just paste in the examples, but I've initialized it with one of them so you can see how it's done. Scroll down to edit the functions.
Site: http://qiemem.github.io/mathart/
Repo: https://github.com/qiemem/mathart
1
@cjfaure The average of all the entries so far is https://i.imgur.com/4kqgQ5l.png - I combined them via Image Magick's convert tool (
– starbeamrainbowlabs – 2014-08-11T09:36:44.373convert.exe -average *.jpg average.png)@gman I played around with things akin to this in MrDoob's GLSL sandbox a year or two ago. Another handy benefit is the live feedback while editing the code. And I agree, I'd enjoy that as well.
– FireFly – 2014-08-11T22:11:18.510