The problem can be solved in O(polylog(b)).
We define f(d, n) to be the number of integers of up to d decimal digits with digit sum less than or equal to n. It can be seen that this function is given by the formula
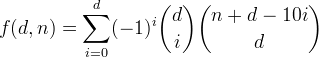
Let's derive this function, starting with something simpler.
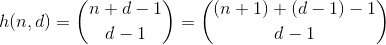
The function h counts the number of ways to choose d - 1 elements from a multi-set containing n + 1 different elements. It's also the number of ways to partition n into d bins, which can be easily seen by building d - 1 fences around n ones and summing up each separated section . Example for n = 2, d = 3':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
So, h counts all numbers having a digit-sum of n and d digits. Except it only works for n less than 10, since digits are limited to 0 - 9 . In order to fix this for values 10 - 19, we need to subtract the number of partitions having one bin with a number greater than 9, which I'll call overflown bins from now on.
This term can be computed by reusing h in the following way. We count the number of ways to partition n - 10, and then choose one of the bins to put the 10 into, which results in the number of partitions having one overflown bin. The result is the following preliminary function.
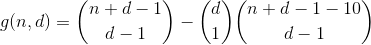
We continue this way for n less or equal 29, by counting all the ways of partitioning n - 20, then choosing 2 bins where we put the 10's into, thereby counting the number of partitions containing 2 overflown bins.
But at this point we have to be careful, because we already counted the partitions having 2 overflown bins in the previous term. Not only that, but actually we counted them twice. Let's use an example and look at the partition (10,0,11) with sum 21. In the previous term, we subtracted 10, computed all partitions of the remaining 11 and put the 10 into one of the 3 bins. But this particular partition can be reached in one of two ways:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Since we also counted these partitions once in the first term, the total count of partitions with 2 overflown bins amounts to 1 - 2 = -1, so we need to count them once more by adding the next term.
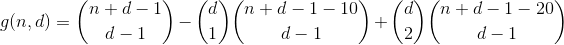
Thinking about this a bit more, we soon discover that the number of times a partition with a specific number of overflown bins is counted in a specific term can be expressed by the following table (column i represents term i, row j partitions with j overflown bins).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Yes, it's Pascals triangle. The only count we are interested in is the one in the first row/column, i.e. the number of partitions with zero overflown bins. And since the alternating sum of every row but the first equals 0 (e.g. 1 - 4 + 6 - 4 + 1 = 0), that's how we get rid of them and arrive at the penultimate formula.
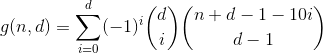
This function counts all numbers with d digits having a digit-sum of n.
Now, what about the numbers with digit-sum less than n ? We can use a standard recurrence for binomials plus an inductive argument, to show that
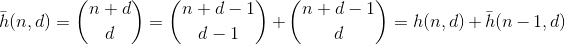
counts the number of partitions with digit-sum at most n. And from this f can be derived using the same arguments as for g.
Using this formula, we can for example find the number of heavy numbers in the interval from 8000 to 8999 as 1000 - f(3, 20), beacuse there are thousand numbers in this interval, and we have to subtract the number of numbers with digit sum less than or equal to 28 while taking in to acount that the first digit already contributes 8 to the digit sum.
As a more complex example let's look at the number of heavy numbers in the interval 1234..5678. We can first go from 1234 to 1240 in steps of 1. Then we go from 1240 to 1300 in steps of 10. The above formula gives us the number of heavy numbers in each such interval:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Now we go from 1300 to 2000 in steps of 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
From 2000 to 5000 in steps of 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Now we have to reduce the step size again, going from 5000 to 5600 in steps of 100, from 5600 to 5670 in steps of 10 and finally from 5670 to 5678 in steps of 1.
An example Python implementation (which received slight optimisations and testing meanwhile):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Edit: Replaced the code by an optimised version (that looks even uglier than the original code). Also fixed a few corner cases while I was at it. heavy(1234, 100000000) takes about a millisecond on my machine.
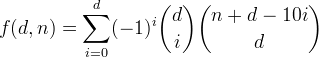
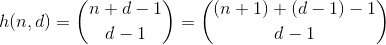
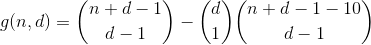
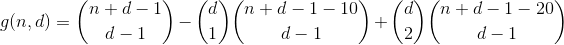
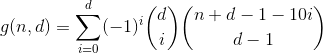
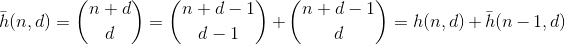
2what threw the TIMEOUT? – None – 2011-03-22T12:45:02.383