5
For more information on Parity: Wikipedia
Challenge
Write a program that takes an input (stdin, argv, ect) of four nibbles and two parity nibbles. Your program should then test to see whether the 'block' is valid, using even parity; if it is then output 1. Then try to make any corrections, if correction is possible output the corrected block. If you cannot correct the block output -1. You can assume the parity nibbles are never corrupt.
To re-cap and clarify:
- If the input is valid output
1. - If the input is invalid and fixable output the fixed block.
- If the input is invalid and cannot be fixed output
-1. - You can only edit bits if their respective row and column in the parity bit is incorrect.
Input Format:
<NIBBLE> <NIBBLE> <NIBBLE> <NIBBLE> <PARITY-Y> <PARITY-X>
So 1010 0111 1101 1011 1011 0111 Would look like:
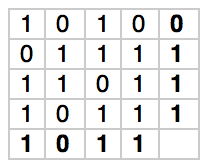
Winning
This is code-golf: Smallest program wins.
Input and Output Examples
Input 1010 0111 1101 1011 1011 0111
Output 1
The Input is Valid
Input 1010 0011 1101 1011 1011 0111
Output 1010 0111 1101 1011
The Input was Invalid, but correctable
Input 1010 0001 1101 1011 1011 0111
Output -1
The Input was Invalid, and not correctable
By "fixed block", I believe you mean "the specific block which is valid according to the parity blocks and can be obtained from the input block via the least number of bit flips". – Mego – 2016-04-28T06:59:16.843
So the parity nibbles are guaranteed to be correct? – Martin Ender – 2014-05-28T23:36:11.843
@m.buettner Yes, you can assume the parity nibbles are never corrupted – Harry Beadle – 2014-05-28T23:55:43.573
Does "correctable" mean correctable by flipping a single bit only? I could "correct" any input to match parity bits
0000 0000for example, in more than one way. You can also correct your example1011 0111bits to nibbles0000 1011 1011 1011, etc. I ask because you use the plural in "...try to make corrections..." – Geobits – 2014-05-29T00:26:38.090@Geobits you should only correct if you know for sure what you're outputting is the correct answer. You have to use where the two incorrect sections in the parity nibbles intersect then flip that specific bit (or bits). – Harry Beadle – 2014-05-29T01:00:53.240
2You may want to add something to the effect of "You may only change a bit if that bit's row/column parity bit is incorrect." I'm still not convinced that outputs are unique for a given input, but that would definitely clarify it a bit. – Geobits – 2014-05-29T01:11:11.760
7It is impossible to know for sure what the correct answer is. When a corruption is detected, it is possible that 5 bits are corrupted instead of only 1. – user12205 – 2014-05-29T01:13:01.113
@ace Correct, but I mean based on your input. You can't go changing multiple bits just to give yourself a correct answer without reason from the parity bits. I mean the correct answer based on your input. – Harry Beadle – 2014-05-29T01:14:32.740
@Geobits Amended the post – Harry Beadle – 2014-05-29T01:17:21.450