Draw the € sign

Question

The goal is to output or display an image with an € (euro) sign according to the following specs (ignoring the border of the sign).

Source: http://en.wikipedia.org/wiki/File:Euro_Construction.svg

Rules:

• The program / script must take the height of the € sign in pixels as an argument (empty space around the sign is optional)
• The € sign can't be drawn as or from a character, directly (it's forbidden to print the € in the image) or indirectly (calculating 8364 then displaying it in a HTML page)
• The output does not need to be saved to any file, it can be displayed then just shown as a screenshot
• Standard “loopholes” are forbidden
• Shortest code wins

Answer 1

PostScript/GhostScript, 100

(96 for the program, 4 for the command-line switch prefix)

Fully golfed and hand-tokenized:

$ hexdump -C euro.ps
00000000  68 20 88 78 92 36 92 38  92 8b 88 4b 88 3c 92 ad  |h .x.6.8...K.<..|
00000010  88 00 88 00 88 3c 88 2d  88 ce 92 05 88 00 88 00  |.....<.-........|
00000020  88 32 88 d8 88 28 92 06  92 16 88 b9 88 fb 92 6b  |.2...(.........k|
00000030  88 b5 88 f1 92 63 88 13  88 f1 92 63 88 17 88 fb  |.....c.....c....|
00000040  92 63 92 16 88 b9 88 0f  92 6b 88 b5 88 05 92 63  |.c.......k.....c|
00000050  88 1b 88 05 92 63 88 1f  88 0f 92 63 92 16 92 42  |.....c.....c...B|
00000060

You can get a copy here, for your own viewing.

After seeing @ThomasW's answer, and considering my program carefully, I realized that I could do it even better.

The tokenized version is equivalent to this:

h 120 div dup scale
75 60 translate

0 0 60 45 -50 arc
0 0 50 -40 40 arcn
closepath

-71 -5 moveto
-75 -15 lineto
19 -15 lineto
23 -5 lineto
closepath

-71 15 moveto
-75 5 lineto
27 5 lineto
31 15 lineto
closepath

fill

An explanation of the optimizations:

First off, I converted my first solution into a union of some simpler subpaths, rather than one path circumscribing the entire thing. I borrowed Thomas's method of inputting a parameter, which is much better than what I had had.

Then I multiplied all the coordinates by 10 and rounded everything off to give me just integer coordinates. I also rounded off the angles, and converted the two large ones to equivalent negative angles. This conveniently makes every single number fall between -128 and 127.

And then I tokenized everything. Each operator can be represented with a two-byte sequence each. And because each number can be represented by a single signed byte, each one also becomes only two bytes. The only part I couldn't do that with was the h at the start, but it too is only two bytes, just the h and a space after it.

Run it as:

gs -dh=200 euro.ps

gs -dh=80 euro.ps

gs -dh=20 euro.ps

---

New: Even shorter versions!

Using encoded user paths, I have managed to reduce the program size by a few bytes. Each of these programs is equivalent to the first one, producing identical output:

92 bytes:

hexdump -C euro.ps
00000000  68 20 88 78 92 36 92 38  92 8b 88 4b 88 3c 92 ad  |h .x.6.8...K.<..|
00000010  7b 7b 88 b5 88 c4 88 2d  88 3c 30 20 30 88 3c 88  |{{.....-.<0 0.<.|
00000020  2d 88 cf 30 20 30 88 32  88 d8 88 28 88 b9 88 fb  |-..0 0.2...(....|
00000030  88 b5 88 f1 88 13 88 f1  88 17 88 fb 88 b9 88 0f  |................|
00000040  88 b5 35 88 1b 35 88 1f  88 0f 7d 8e 0b 00 07 08  |..5..5....}.....|
00000050  0a 01 23 03 0a 01 23 03  0a 7d 92 b3              |..#...#..}..|
0000005c

Which is equivalent to:

h 120 div dup scale
75 60 translate
{
 {-75 -60 45 60
  0 0 60 45 -50
  0 0 50 -40 40
  -71 -5
  -75 -15
  19 -15
  23 -5
  -71 15
  -75 5
  27 5
  31 15}
  <00 07 08 0A 01 03 03 03 0A 01 03 03 03 0A> 
} ufill

And a slightly counterintuitive confusing solution saves one more character, for only 91:

$ hexdump -C euro.ps
00000000  68 20 88 78 92 36 92 38  92 8b 88 4b 88 3c 92 ad  |h .x.6.8...K.<..|
00000010  5b 5b 8e 1e b5 c4 2d 3c  00 00 3c 2d ce 00 00 32  |[[....-<..<-...2|
00000020  d8 28 b9 fb b5 f1 13 f1  17 fb b9 0f b5 05 1b 05  |.(..............|
00000030  1f 0f 7b 92 38 88 7f 92  50 7b 32 35 36 92 a9 7d  |..{.8...P{256..}|
00000040  92 54 7d 92 49 5d 92 32  8e 0b 00 07 08 0a 01 23  |.T}.I].2.......#|
00000050  03 0a 01 23 03 0a 5d 92  32 92 b3                 |...#..].2..|
0000005b

Which is equivalent to:

h 120 div dup scale
75 60 translate
[
  [
   <b5 c4 2d 3c
    00 00 3c 2d ce
    00 00 32 d8 28
    b9 fb
    b5 f1
    13 f1
    17 fb
    b9 0f
    b5 05
    1b 05
    1f 0f> {dup 127 gt {256 sub} if} forall 
  ] cvx
  <00 07 08 0A 01 23 03 0A 01 23 03 0A> 
] cvx
ufill

Answer 2

Mathematica, 193 183 177 173 169 166 bytes

Yay, maths! I'm plotting the region that satisfies a certain (rather complicated) set of inequalities:

e=RegionPlot[(1<Abs@y<3||c)&&{x,y+12}.(d=2{-5Sin@40°-6,m=5Cos@40°})*{x+15,y+1-2Sign@y}.d<0||c&&x<2m/.c->100<x^2+y^2<144,{x,-15,9},{y,-12,12},Frame->0>1,ImageSize->#]&

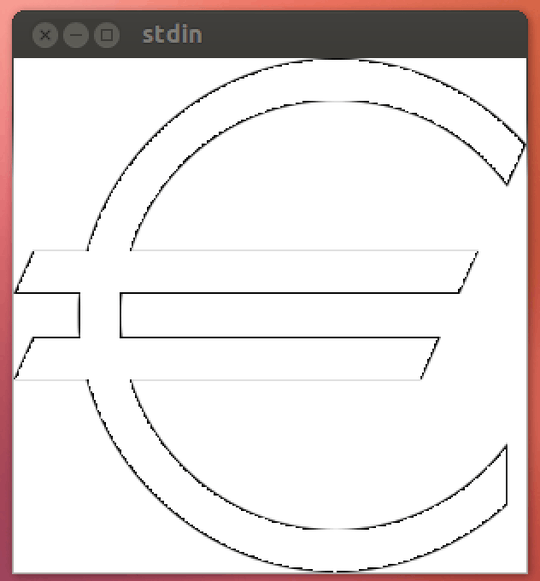
Usage is e[height], e.g. e[100]:

Or e[200]:

You may notice, that the sharper edges are slightly rounded off. That's because the region can only be plotted by sampling the points in space, and Mathematica doesn't sample each pixel by default. The sampling resolution can be increased by adding another option PlotPoints-># (which uses one sample per pixel), which adds 14 characters. I don't recommend running it with that option, because it significantly increases runtime and barely increases visual appeal beyond #/4 or so. Hence, (after approval of the OP) it is not included in the score.

Here is a slightly ungolfed version:

e[height_] := (
  angle = 40°;
  d = {-5 Sin[angle] - 6, 5 Cos[angle]};
  RegionPlot[
      (Abs[y] > .5 && Abs[y] < 1.5
        ||
       r > 25 && r < 36)
    &&
      {x, y + 6}.d > 0
    &&
      {x + 7.5, y + .5 - Sign[y]}.d < 0
    ||
      r > 25 && r < 36 && x < 5 Cos[angle] 
    /. r -> x^2 + y^2
    ,
    {x, -7.5, 4.5},
    {y, -6, 6},
    Frame -> False,
    ImageSize -> height
  ]
);

Note that in the golfed version, I've scaled the coordinate system by a factor of 2 to avoid the .5s, but it turns out that the character count is actually identical.

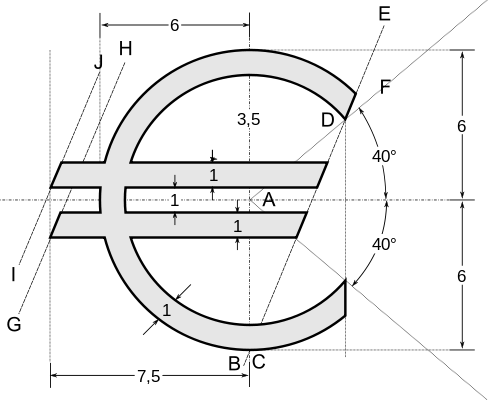
Here is an explanation for how I worked out the formula. I divided the shape into two regions. One contains the ring and the stripes and is cut off to the right with the BCDE slope and to the left with the IJ and GH slopes (more on that later). The other contains the same ring, but is simply cut off at the x coordinate of point D. The conditions for the two regions are combined with ||, which acts as a set union here.

The ring is just defined as 5 < r < 6, where r is the distance from the origin. r² is easier to work out though (x²+y²), so I'm using 25 < x² + y² < 36 to get all the points in the ring.

The stripes are between ±.5 and ±1.5. We can handle both stripes at the same time, by taking the modulus of y, so the stripes (of infinite length) just fulfil .5 < |y| < 1.5. Again, to take the union of the stripes and the ring, I'm just using ||.

The interesting thing is probably how to get the "masks" though. Point D has an x coordinate of 5 cos 40°, so the mask taking care of lower edge (combined with the ring only) is just x < 5 cos 40°. This can be applied via set intersection which translates to && in logic.

The other masks are the really tricky part. First, let's get the slope of BCDE. We can easily construct points C and D, as (0, -6) and 5 (cos 40°, sin 40°), respectively. The vector pointing along the line is then just D - C = (5 cos 40°, 5 sin 40° + 6). To apply the mask on the right, I only need to figure out if a point lies to the left or the right of that line (let's call line vector p). I can figure this out by taking the vector from C to my point of interest and projecting it onto a vector perpendicular to p. The sign of the projection will tell me the side the point is on. Obtaining the perpendicular vector is pretty simple in 2D: flip the coordinates and reverse the sign of one of them. That's the variable d in my code: (-5 sin 40° - 6, 5 cos 40°). The vector from C to a point of interest q = (x, y) is q - C = (x, y + 6). The projection is just the scalar product (or dot product) between q and d. The way I chose d it happens to point to the left, so I want d.(q-C) > 0. This condition applies the right-hand mask.

For the left-hand mask I can use basically the same idea. The slope is the same and therefore so is d. I just need offset my point from the lower-left corners of stripes instead of from C. Those have coordinates (-7.5, 0.5) (upper stripe) and (-7.5, -1.5) (lower stripe). So that would call for two independent rules for the two stripes. However, note that all points affected by the lower mask are in the lower stripe and hence have negative y. And all points affected by the upper mask have positive y. So I can simply switch my offset using Sign[y] which is 1 for positive and -1 for negative y. So my offset point becomes (-7.5, -0.5 + Sign[y]). Otherwise the mask works just like the right-hand mask. Of course, this time the projection needs to be negative. So, naively that would be something like RH-projection > 0 && LH-projection < 0 (which is also what I originally had in the code). But we can shorten this, because multiplying a positive and a negative number has to give a negative number, so it's just RH * LH < 0 (where RH and LH are the respective projections).

That's it. Putting it all together leads to the following logical structure:

(
  (is_in_circle || is_in_stripe)
  &&
  is_between_left_and_right_mask
)
||
(
  is_in_circle && left_of_edge
)

Just to be clear, the coordinates in my explanation refer to the construction diagram given in the challenge. As mentioned above my code actually multiplies all of them by 2 - I changed it to save bytes, but the byte count is actually identical, and I couldn't be bothered to revert the change again. Also integers look nicer.

Answer 3

BBC BASIC, 202

INPUTh:w=h/12s=w/2.4p=25VDU22,6,29,640;400;p,4,0;1.5*w;p,153,6*w;0;p,4,0;1.5*w;p,159,h/3.1;4.7*w;p;9*s;9*w;p,87,h/3.1;-19*w;p,4,-7.5*w;0;p;s;w;p,85,4.5*s;0;p,81,s;w;p;s;w;p;s;w;p,85,-7.5*w;2*w;p,81,s;w;

download emulator at http://www.bbcbasic.co.uk/bbcwin/bbcwin.html

In BBC basic, all graphics are handled at the low level using machine-specific ASCII control characters (but some high level commands are also available for the common ones for convenience.) The ones used here are 22 (change display mode) 29(change origin) and 25, equivalent to the PLOT statement, which takes an additional action parameter (draw line, circle, triangle, etc. in background/foreground with relative/absolute move) before the X and Y parameters.

So all I have to do is send a load of characters to the VDU controller. values terminated in semicolon are 16 bit. others are 8 bit. The total number of bytes sent to the VDU controller is 91, though that in itself would not qualify as an answer because by that stage the size is hardcoded.

The obvious place for the origin is the centre of the circle, but there are actually more commands involved in producing the bars. So I shifted the origin down 1.5 to the bottom of the lower bar, which reduces the number of fractions and negative numbers required. It remains on the vertical line with the centre of the circle, which is important because the line E starts from this vertical line.

Actually, I only had to calculate 3 numbers off the drawing: the top inner corner of the C shape (5 cos 40, 5 sin 40 + 1.5) = (3.8302,3.1394+1.5) = approx (12/3.1, 4.6) and the gradient of the line E:x/y=3.8302/(6+3.1394)=0.4157 = approx 1/2.4

As I only have the free evaluation version (interpreted), I take the symbol height as user input. If you buy the full version (29.99GBP) you can compile and then read the command line with w=VAL(@cmd$)/12.

Ungolfed code

In the golfed code, there is only one VDU statement, but in the ungolfed code I break it down into several for clarity. Also, because BBC basic is little endian, the combination p,0, can be golfed to p; but I left it ungolfed for clarity.

  INPUT h
  w=h/12                   :REM w is the width of the line, which is 1/12 the height of the symbol, hardcoded at 900.
  s=w/2.4                  :REM s/w is the gradient x/y of line E. s is the horizontal offset of the top and bottom of the ends of horizontal bars
  p=25                     :REM VDU p,action,x;y; is the equivalent of PLOT action,x,y

  VDU 22,6                 :REM change mode
  VDU 29,640;400;          :REM set origin

  VDU p,4,0;1.5*w;         :REM move to centre of circle
  VDU p,153,6*w;0;         :REM draw circle in foreground colour
  VDU p,4,0;1.5*w;         :REM move to centre of circle
  VDU p,159,h/3.1;4.6*w;   :REM draw circle in background colour, ending at the upper inner point of the C shape.
  VDU p,0,9*s;9*w;         :REM move relative along slant gradient, 9 spaces in y direction, to define the upper cut on the circle
  VDU p,87,h/3.1;-19*w;    :REM draw triangle in background colour, based on the last two points and the absolute point specified here (vertical line for lower cut)

  VDU p,4,-7.5*w;0;        :REM move absolute to bottom left of lower bar
  VDU p,0,s;w;             :REM move relative to top left of lower bar
  VDU p,85,4.5*s;0;        :REM draw triangle to bottom right corner of lower bar (absolute)
  VDU p,81,s;w;            :REM draw triangle to top right of lower bar (relative)

  VDU p,0,s;w;             :REM move relative to bottom right of upper bar
  VDU p,0,s;w;             :REM move relative to top right of upper bar
  VDU p,85,-7.5*w;2*w;     :REM draw triangle to bottom left of upper bar (absolute)
  VDU p,81,s;w;            :REM draw triangle to top left of upper bar (relative)

Answer 4

HTML, 250 249 248 242 244 234 229

<svg viewBox=-7.5,-6,12,12
onload=this.style.height=prompt()><clipPath
id=c><path
d=M5-6,1.8,1.5,3.8,3.2V6H-9.4L-7.1,.5-7.5-.5-5.2-6>
</clipPath><g
clip-path=url(#c) fill=none stroke=#000><circle
r=5.5 /><path
d=M-8,1h15M-8-1h15>

While this is only using SVG stuff, it heavily relies on lax HTML parsing and has to be served as HTML. Strict SVG would require a lot more bytes.

Try it!

Answer 5

CSS, 512 494 bytes

<style>*,:after,:before{position:absolute;width:20;content:"";background:#fff}#a{margin:150;height:20;border:2px solid;border-radius:20px}#a:after{width:10;height:10;bottom:0;right:-8}p{top:7;left:-6;width:29;height:2;border:solid;border-width:2 0;transform:skewX(-23deg);margin:0;background:0}p:before{width:2;height:4;bottom:-3;left:-.5}p:after{width:16;height:16;bottom:-3;right:-8}</style><div id=a><p><script>document.getElementById('a').style.transform='scale('+(prompt()/24)+')'</script>

Not the smallest answer by a fair bit, but as small as I could get even when summoning all my css-minification-fu

Caveats:

The above code with all 'px' stripped works in Firefox & IE but not Chrome & Safari which are fussier about their units :)

I also had to re-add the px's to get the jsfiddle to work:

http://jsfiddle.net/9A3J9/

100:

200:

ungolfed code:

 <style>
*,:after,:before{
    position:absolute;
    width:20;
    content:"";
    background:#fff
}
#a{
    margin:150;
    height:20;
    border:2px solid;
    border-radius:20px
}
#a:after{
    width:10;
    height:10;
    bottom:0;
    right:-8
}
p{
    top:7;
    left:-6;
    width:29;
    height:2;
    border:solid;
    border-width:2 0;
    transform:skewX(-23deg);
    margin:0;
    background:0
}
p:before{
    width:2;
    height:4;
    bottom:-3;
    left:-.5
}
p:after{
    width:16;
    height:16;
    bottom:-3;
    right:-8
}
</style>

<div id=a><p>

<script>
document.getElementById('a').style.transform='scale('+(prompt()/24)+')'
</script>

Answer 6

PostScript+Ghostscript 137 + 6 = 143 (binary), 209 + 6 = 215 bytes

Fully golfed version with binary tokens:

$ hexdump -C euro_golfed.ps 
00000000  68 20 31 32 20 92 36 92  38 92 8b 37 2e 35 20 36  |h 12 .6.8..7.5 6|
00000010  92 ad 35 20 36 0a 31 2e  38 20 2d 31 2e 35 0a 33  |..5 6.1.8 -1.5.3|
00000020  2e 38 20 2d 33 2e 32 0a  33 2e 38 20 2d 36 0a 2d  |.8 -3.2.3.8 -6.-|
00000030  39 2e 34 20 2d 36 0a 2d  37 2e 31 20 2d 2e 35 0a  |9.4 -6.-7.1 -.5.|
00000040  2d 37 2e 35 20 2e 35 0a  2d 35 2e 32 20 36 92 6b  |-7.5 .5.-5.2 6.k|
00000050  37 7b 92 63 7d 92 83 35  2e 35 92 14 30 92 6f 2d  |7{.c}..5.5..0.o-|
00000060  38 20 2d 31 0a 2d 38 20  31 92 6b 32 7b 31 35 20  |8 -1.-8 1.k2{15 |
00000070  30 92 85 92 6b 7d 92 83  30 20 30 20 35 2e 35 20  |0...k}..0 0 5.5 |
00000080  30 20 33 36 30 92 05 92  a7                       |0 360....|
00000089

Download hand coded binary file

ASCII version:

h 12 div dup scale
7.5 6 translate
5 6
1.8 -1.5
3.8 -3.2
3.8 -6
-9.4 -6
-7.1 -.5
-7.5 .5
-5.2 6
moveto
7{lineto}repeat
clip newpath
5.5 0
-8 -1
-8 1
moveto
2{15 0 rlineto moveto}repeat
0 0 5.5 0 360 arc
stroke

Save as euro.ps and run with Ghostscript like

gs -dh=80 euro.ps

gs -dh=20 euro.ps

As there is no such thing as a pixel in PostScript, that height is interpreted in points instead. I calculated +6 for the switch on the command line.

Answer 7

PHP, 432 435 367 356 334 bytes

_{(Edit: Apparently IJ and GH are supposed to be parallel with BCDE. Now fixed)}

This script outputs an SVG image, but will serve it as text/html by default. I think most browsers will treat this as an HTML web page containing an embedded SVG image. It seems to work OK for me anyway.

The height of the image is passed as a query string parameter. (Note: the byte count includes a newline character at the end of line 3, which is necessary for this to work properly).

<?php $x=$_GET['x']/12;$a=$x*5;$b=$x*6;$c=$x*7;$d=$x*12.4884;$e=$x*2.2863;$f=$x*5.5;$g=$x*.4157;$h=$x*6.5;$i=$x*7.5;$j=$x*12;$k=$x*11.3302;$l=$x*9.1628;$m=$x*8;$s=$x*12;echo<<<Q
<svg width="$s" height="$s"><clipPath id="c"><path d="M$d 0H$e L0 $f L$g $h L0 $i V$s H$k V$m H$l z"/></clipPath><g clip-path="url(#c)" fill="none" stroke="#000" stroke-width="$x"><circle cx="$i" cy="$b" r="$f"/><path d="M0 $a H$k M0 $c H$k"/></g></svg>
Q;

---

Updated version (367 356 334 bytes):

preg_replace_callback() is a much more efficient way of scaling the numerical values. This code produces the same output as the original version. (Edit: Further reductions thanks to Einacio)

<?php
echo preg_replace_callback('/[\d\.]+/',function($m){return$m[0]*$_GET['x']/12;},'<svg width=12 height=12><clipPath id=c><path d=M12.4884,0H2.2863L0,5.5,0.4157,6.5,0,7.5V12H11.3302V8H9.1628z /></clipPath><g clip-path=url(#c) fill=none stroke=black stroke-width=1><circle cx=7.5 cy=6 r=5.5 /><path d=M0,5H11M0,7H11 /></g></svg>');

Output:

euro.php?x=60

euro.php?x=200

Answer 8

Python - turtle - 517

import turtle,sys
from math import *
q=sqrt
h=int(sys.argv[1])/24
t=turtle.Turtle()
z=t.begin_fill
y=t.end_fill
x=t.goto
w=t.towards
v=t.fd
u=t.circle
r=t.seth
o=t.setx
n=t.xcor
t.pu()
x(10*h,0)
t.left(90)
t.circle(10*h,40)
z()
A=w(0,-12*h)
B=2/sin(A*pi/180)
u(10*h,280)
r(-90)
C=n()/h
v((q(144-C*C)-q(100-C*C))*h)
D=w(0,0)
r(D+90)
u(-12*h,D+135.42)
y()
F=2*pi/9
G=h*cos(F)/(5*sin(F)+6)
x(45*G,-3*h)
z()
o(-15*h)
r(A)
v(B*h)
o(45*G+15*h+n())
y()
x(65*G,h)
z()
o(-15*h)
r(A)
v(B*h)
o(65*G+15*h+n())
y()
t.ht()
input()

python % 100 and python % 500 respectively:

Answer 9

sh, 8604

I think someone can probably do better, but let’s start this off.

echo /Td6WFoAAATm1rRGAgAhARwAAAAQz1jM4H+YGLhdAB4Py4cR2M5mkQ+DHsr9ezPUf+m32igxdiVmIE0qCW1q9ylwOEETlQiK0Fsdk0viUoZ92eYvWaMHdwLoMvi6YDwnr8S/yxLAdptt59wmMVhiurpONaAjMQ9GMfk6S30qx7jrBFm5ec/+Hn3vgsK40Jb07a6/0rVXAFjJIovBtvKPxLBzhck8dVbcobncgkaX2KwqKMU/iP53UquQVeD8Nge+b3lxQ6sFl9unjQy8r1YpGcimh121n0ukvQ5j+QnWIWoLj0v3NigOOM277wOfPQkw0oxC6AA3EB18EbFisDx4CJQKfK9AGsEYoh+ILP4UnIQrlecXuly9QXblNneSkZ5FNB2XlHBxuYAPnkQl0SU/vOWtozgXSyYgwgGabdR0/K/2m8Tm9xiiqGe+HwD8zzaEOB1anMtUnFRupCUCjyl1QQ8Ca2QkLTEo7S7oPCYh6y2ztXdsIBWCvYEHa0OLIuX3t5s7DraSjYGlbiCQF0mJf4KFFBR5TXwUQxq2YHfhNHRitStzvemCYBAYNbQ3Jv6rVibvg54pYu9hdX0pqQsRABX39jyTDiizCbMOs/mFveZqDUT15nvIjsC1Z9i9fJFA1uHYgVZYZKXELaRD/umATW4sK5ADKUeoFzDYfozSjhVZMe8uZ2QnafbwCHdaDxMDq1qkabmhMV9Xa73iKNZlf/3AXXaQNe2zTLixO2UcXOgW7eJ2HrtOCXqSbWWSlDzDmycDelezms0hK7qleLNapDHZFuvr8MoVvuikKjkAX3Cc1DKnwS5wtWjn6wlx+5Q7LNQjS79ccEo9H/aPQ1mbPwekoefgMdFVYMKXImJV5EGn5p7cw1H/BScuwgzk9dV8vnpnVCz+HqeIG0wSXuBgipP548iAclUncu/NYqe3M5q19PXIsaSed44ScJn97yMdYbpjhb9J/34c1/1nIZMgFjAkAXbaOglmGTNC0VQo7/CubHyXy5OJTiyHqNUfskOTGP1A/Nla3Nag9gzKK7yiTimKbJCaZj5JcviByWuKguR/uAiDLHIAPFS9R96JeNYJEg9JyWjAMU2nSSS3AFDKpNIqNr3NLKd1BLo8JyPpnfCJswwgs1RjsjTk0McOTTeAKfEMhWlEXlNKcCV9eLunwwv7Xx5azMOUpO8KKZ5XBXZZafai1FbQqKY/0RRJ1sa6l/2YEq6hhNuiJ7KqrCM7pwXNFXUriO5o2tUWt/lgHOV0ronovl7yrPp5xUcAudDnNcZP6H9QoDiFjhidBOBsmObzQfCHlS+sMcN1t+sP3JLUxFv5jKCBFT+pjtGyugg4H8EKT4qz/V+LNEKR3FaS9SPxTq0k8sDo6PlxcRfXxkgyJ5stYsqVrLGmkeoGy0OTQ6y1lkmC5+Af9Oo2HvCvW4a4SBMobiZvsTNRzJxTh4k8drMHhYMkT8R+WGT2c9GvPmYwBSjh/NVxrT5twHKpjLB/ZsUU3+mGfkU+H49DNnHxXAla4UL3Ivp4GviWgl65SkyxfCIl678h+nIN07rvgGrSX7bt+wCvsKnIioXR+k7VYv88upJnIcjQepEtkZSCwwX81KTjdugGDt2NnWJM7wAWQjzx+wAOp1k5Lz3dEDpOXlsuOvTuNOY9b0FyBb8HF+cmWaRNKOvmbBvf4yITqthVM8PtKqYEJKwoTEm2ewAGTHcct8y7SMWnWjwdxiS9vFl2i1yWtpon54IY/uiyjyfm4HG1eO/zklccbKCkS5JnCNY1FfqKYxaGzAhjWOmuEgitjtnNJ9m1vFyllOaaWNal/otis6OD5pVG3xWbqgQVxCQZlpZcFlUvFGaQnGeDgGqzGb7mDNCMrMff+1PTjY/oKqPcwBEQl2e+aSYw/WKwJBnicO2G55kFDwfLZivL8Ye+Q1biPrJz6jUoJNVOM6jPCBQXB/1rtZiNIXcFi0oEmTs+rXPE1pijmYKWAac7+U+O00ZOHhKq+RvnpL7Hjim/stmcaDvuS2nMz6Yg8Zf0vhgtDz8OYLUWCSMMAomV8er77ODjjlRl8caLpkv6nO/kUoYoQKXztM+vQDcYujpwIJ95IoLQGrZ8niKRn3+NbfCmeSSPV3NczkBOkdZqa++NLFPV7WENQTNvlMwl8nhHbC7OIrkIitozEye0a7UevgQq4GcBYIRP4x0nMr58zoe0TqaCXL+jsfoeZitanO8y3tDCLGCLwhuuB1K4hMgy623pJCejc2UfB9XYPJqNgqm+GFFsPA1fuuypqQ7TTS/CUcT2iYxa/ksAvA0LhyYkHTll/vZoot06nt+JVnHShH3VJknmeiNku1ZBhq8gcZ3TcIuaNWEtK90P2Ah+CLIBA/k1oNlG289CeH+R5FyflWgV8XTiBDCcVC/zkiENYIW0ajAqvkBWuUvfgV+YEtmwPTVtE8oJu7IDDR5YN15OE4KWL0pnub2qOG/NAXcYxbHmS1sza6la4N+K17WInU/H7ol9INu7bH6WVZD097WHdjbi8UPHsbM88Jr9pmMPKPNlsDZD+ih154RWSLTVcjZA0jSzChqiNm0bW+0EszFDarF4tGauJtDqnRr+0t3QwC56VcRJzrCpJwkcp1NvIKHY11KRJ+mvA0x23KQijA2BPOICPYJ23z7CZLyoIkc51eXgjMVJbg3T1wrXtCMuhkwlcQ1rO8KVg3ajLk4dsyF27LaVjQFkxbHYIxhQXmRGgsMo2cO7bUuwLyYMEDKEQJgsDGj4KQIxLV+MVH5U9+ttKfBDuYc1ZKc1pVcnEWZ5vWRFHlCFfnD9Au0EIgfEu0hzx0e1JpXY73iOyahpo/yKj+FbKzVBPq99RLokDrlcOvBnG492+464GDCbQvdJQtbiYHU8bSHXLyMU38qh1IBlu0ecIKnfL426oKtyZ5TkAPaj5mELf15dRg8V5t2XL4UnjHzUryz1d3KfHcrO14AmP3Ne6YKUAXOx9H3f2xm6N9mEPvC2R9wGgvuTabZ4V9HcTR6EtjXDHzW/ZjrU0JgA5j1t8+6I4DX8mWqC1vQxUMLex5xnJm2vIcxBBf7QceJTTsKq4V0T0a6Mxc9rR9WnS9Yfma4c2Zg0voJqJ4AmkJI9IqWx5Z+WV8Ddfo0ybRM+zuOtBpWwN20Ipn/IEl+FgMp2vb9bJ60umzK6rx/KyfkcK1eT3UdS7ujlOUXSvSol5ctj8E+WEds7KSxZ6jaW33SitKUuhUOFCnE9/Uzg9DSyeSG6p3/TtymeYTUgzGFtHCRtEhQdqlmuLORmEi1WB7lDop+UaiVeZ8cdL8BUtzIrMhCYY+zbsexxUtYY0xUxRIVVGuvry/rZjwfJtIbHhsC0XvhX9ycR/kViYZYkfS240arLfwjxMtBGfpbKcY64hZOQnTA2jFIGZDWrF1frAZV94IYacIb5rIkwwp6+P3fP3kNQ5wMNXtiaJ7PiyWZUHijkNzaT2hkydrJ8cfO+m8N5OUsJPUIOZ/sa7Zx/HmHOGc6CWkSU9rJfCDLxXCTMGL9ubU6RX7Zr++sjXIFGWkVrflysVVdQ8n9ifEyFDeX/r8YoKj2S2T32/jACXwySEsd/rEoYgJcOnHo/NuLnk1LZxt6S9D8GUqy342fzhXaPL7+Xy53/j03+7YlooLsZH+oTtid0ijLlRtSFwQtlJa9uusHfP+GnBrJplJyunwnLTtQ+QC8BgXXB+p5cTiJ3BfYUco/yH+aFcRtQZ0IXRk0z0BN7A1R5fWcnBvgbjJJBNN2RB5MWqtRTctGPJeHPylI4j2Pa2K0qm5pGrFFWof8LcmsQGTtnGm5AUrGBCaVk0WxgZMY1Gqqls3UoeAy3+NWdXHJPz70I9vHvB+CiUhAzGs+B/9YPRrTpS9lMOioHRrRgM7k+WDOFhKs2ZPaxlWk7LqGpf8yISw0U0uYyXYFCJcLIeVYz5yKYGejVaKQEUQOvsxJf7E/SVHcG+o60pe0e0ONCub8ttIw17Cehy96JUO50bD62BkgtepSAg101mFMTo5EfvxSZ5mcJk1dQKRxR5pkHNlmUuPHdrBm/t1HgN/HQ37aNRYrZGWGRgUVMBgZoCHu6ZQ/NLtoFs75pxa8TDZ2N1KVngWCsUI0WT+ouyhRSixloz11fihaHRIaTS5VukEVcXosOzdhlka7YmhWxS0f0y7LfW1ugBxecKuSrBzsFa7hVM/iEYldMSR7ozzhhLGHRnVOc8yECM3CvEgE3qcS86jJA4+tjCW2CViftkQbVQ9xUJZeALqNF6bkFqknmwbiCVGkpNYjon4I46XPUl+7Fm8YLy2+VHTn2uMFhE9vGfqfgIS5PAyMttOB1iFxgljxRpQfI2jqwzEscF0v8IPVnZMrk6Otcrwq0kW27aR2NIElOBq/7Na5WlvFniNITn45BTSCNWm8ijx1VQR/cpRz0TlPwChXj1x6rACGII6hVWcd4MBWL/oOIGW/Yfj6CFuAU7hQrAH/Wk+YF6920XeFTTtzusQnqS/Ha4bE5tLZsPW0Bv53oFohSbBZexHufmkIO4wzfgEsH//T6X8vdCx70gDV5leqt+Wrpbkh6fo8IJptuGjnuH0oPUcTt5e/77Yn/PsPsjqjC7RQhSsDugi4GIbbEN7SdBbS69zg7NeN5lI53gZfN+mjcXCQzhC9J2DmYWmqhJ8XblMbAvcrARtQWBKZuOLSzgRkAToONyWndfTy/n/QpBJPJmF2KkUAncc9t4e8I5zdzClXBKQb6O1AIuDTs/M7mX/MdB2tHEqenLoOD+V9sTdT86Uub0BasAh0R5hvi2Iorm7llfPjy3aGbbogeN4J052oZx1aBTWTbUgX7vi2v6+ijQIMd4WnxYcIgebIZAZIHzjf+e28h3TXHyQIj4ExFH73KtUmbeEBmfmby8mGavm4SmmcMrVtlQflXYa1cpzm4ou9N31ARgxXMBNLbdmeWNSZ7Cjww8SX3ranoZGKofMJ/GUNEW4m/zyDyb9d7QPRIKYc56dWffu/7VhmlqAWrTJPNoi+vJSWe957pRibDGVaxcsHm36AVEffhabj3BsIkFnRGBozsQX+15QkpOqGy/gONQNdzQR7gdHDfo7XqhrbgvTwgNhXNITA39pWovQ+3izHtqSwQp6qKHa79WfPPVTYyZ0C97yUvOsRBWd9upeF6lIycXQYZyqx6YGB36HiyOZi2DNDGN457CZU+41UsLsbrliLrK5jVf8TiGjC/JcYZ6OZ8R2cASh1yK+746LUdQdQt2oRUZBuL5b5aMAuSyFM7AyTR/pL8vUYjGRAsO3jp1HLldgJPK8Sd8BzbbAza9FpPtvZfWXmgRhSqD6cH7hsG6p9579iOtJWNBNDJXnM8KZOICYFYvaiqSy+yFb55Xz4OBO+c9n1+Kru7DVpldr7D+3PZgrvwiVxy3pDC63pIzGkEkCyUNOVB2/a/3cjYgnBOI2rcMqnW4QOkvEjtG0LCQ99R5UJgxAovxs3mJvWI4MTPGVmOKC78jMaltZFSVOQJClEMbxsJ0ZiCBu3LlwKo+eYXfQ541G0+zBD6vGw8TVTwdx/Pv1UvGPOwJyoDJ4wwDxcxUvJgGTEOXS/Uf/VXJYcxPXi5K9bHGCXQx555XTkz63DxHXndKVDifbvW8uVOMLwr0RH36QeAXJmaeOIhUY80lDuvwHH5KSakMoknHbAqbzQRgYovZflW80b2FL1deHFmagseXjj7dQPwVlM6g+JbIH06PoRV/KLnzoTGx/XayzXOntWuNf6M+H8rDJwSTC8B+zGEe0PHPEWi7JmFTXpX5zE7wn3v5kHl9dq9yKof5IUUxOrQgErFxiZjDIptmjfaCiZ6j7gaNdfCLQvOOna4/Z65Nw9M1Uk+/BjrygmO2fansroWxBwCzGmQYHIaMko8+NYesi5Xr8zCptzh00NbPqclbr8Ifc20Uyr2oOcuNL//8mgrDUhw8YdGscmONcc7SgA52V5hh5M8cftXGgYUtyZCa7tmU3bCvBiQXhUA1c3pld8g1Isjncr6BvikWEDwZF5dGSNfnZcvcI/2hwEWhUbq12T3+a8fs9XWPHRHbJ3SCbJF6nGAMmyeDmOqKs41lmQdWwLcGhNicyhgfJrP+wHgnyUavSItqMXfAj/0b/jut1wzgcuxivQzARFCmbODeMCTljqSRIuAHEpC+OPXkz/eZFVRxq4+sIx5CnuDPnu+FAFBAJLlfy+B3gpDGSuHhJzxAVbBQASI6eAAkn0cjokCpBNEEhtOWihPzE37rlSBkFpA6W4/gyhqOQmS8AcyFkrK4DZERHy72p7p0pthswVZpebykXA6fqHw9qJtNzFS3A65Z+Fn4qIqZvxBKIfQDz3GnwnUs2uxZUubU5Dzx5vYVmXvs0WSbFD99m/iYyHWfgVi+SPxjoRW/wx6WEF966pDTwH1IAQhIpQcMO5SfdY51suPqlhquRTIyWnut+laWzca9A1rfj1ODW08jjvRk5zclGNhC6dIOU/2YRr52QIV6uDla4Fhk6P0cspyt4RKJPeazjhQ6iYw3QSgoPrxpcuGhwVKQfm4G3F0LHmuSNxJeMlP5KBACT6z/yyxpLONblrmLX7eoLEpuvuW2Oh2i3ap9NZm29p6f9iS24z91DKqbJoq7kI6D0QWQNPo+V2XvrcJ2LUbHiAysLzxcOoAELuDYqzkhEFTcC00vYHYbx22uHQ6BDmdHWD+pQxLsZI6cbRkKlrGanKXDJ4SzyWgIB6k729GDp7XA91FpBRQ8DVXeGIkzLHnSkYSHD9p5pwtBl9u2xxxmTVfriCDlmfeAKISOVNCWvI5GIaIWc2K2cokE/1ybo/ZCzCl4U7cuKS7mvFaDzcYhTfLfeOpS7DE/ikpG9at1Dx3XVlUKguskbKNYeiqvYctwxQwbzhcfZkDX3cFoZoYlZIT/QeRf+aUDCxDFdf9+ToFntaakEVsg3JJw4iplscbOyzxL9TErqGuEKDKYF6o0dIpco06a49C9ICOQUGxoMnhYHLfi8bo6g8egxWERk8Y/up9F2pnVdz3++jFAb9ODuWvbdOMepygUyIk8Cg6/AV2eBHR1gCvAd+x+b8mSqvnV9UqtQdzsDj5hZNzTERgSfEf9ZBBfwgRChD1Q+f2G0l4ZpYqoeOJVbH2BRubZN0peLfkv0FpydayYg/fxdafPq1DIprP3nDrn9BkPFRGZpmCmpJAF8SoPl+fX/w0a0FySW2ygWxrNwdR5EMNSFBAp/nLMaDZSQ9LxsskgiypkMpLvDt9VrzJs/hdSKv+JDHPuuUf17BWFwGTNg4OImamKEVYWbGXhAmf1NCnsCN41nuUrhYrKpucVerzYUBqwaAj83+W90UNh5jmz5EeZdkMYRE83ij1ClWzQVtwp08wGjX/MqZTVmF0gaJqoRa0BeBtBJGifEUnxfyN1RroM9g0Y7T7CNETwPkBCyMB/jQsFu2OaEzhToBg/0rIOScmuhRD4JSjsbgs5ynZm5ci1JUsbqq8HcBxO0HfnjxZ6wPQlT9hkfH6Ymva1n/XOhArB4l7GItVzvLg1ZImgTf8Nq0sn/nKEARVhSwkgwd791oZ/F9SBGbhU8+wk+x7OeZGIh3LJPVmGzbAPcfcK9WznajPvroiXT5l4MaqOd451yCOthi4BgBVadd8Bq9tNXhQ8AflUWHOUOm3EL90V/ARPFWu96Y325Dw8VwLh0751C5anEYmI7toxBwl0AmAaL9cHFFgLzVr93+8giYfgmcTywXw4tjZJAnIZmlhtBfikAyN9olQpFP7XFAY0KtYOHAeXX+hZPDdGixhaj/0LEHFIs3dNAUFLt+iup+iiDooquvX2ZKOU66j621MQhvML9qNo1EwtmzLyTG3UnSY0YHuifvbqdH+JE9OJAdFA4p7LhTPU3eB1QpXdNx3F/1Epx3EiC+o/uv0aTDj/zmppkPhcok7sxEn2cXkdkaauokaxz57ewlC5ErqzL0KhM5xYcsSM/u4Mi5/9errCGJfqoB9F4NVE12yj21mXv+kqYuakLcn2IE435bDkyf+20ChP3xTyIo5WP1elNQF+AsvZeqvNvthSGhiQfOxwMX1eklBCS0fSsfW77xT67D3G84cpu1tTZegdVEcpoy2fk97NbhNK+HIYH7Lp+qHyBXkdu0cRr6/lZScyUKnKmasdWGOXVgvRUNFOYzKebjyunfFKUJUmzZe9cKFOeZsrimtMzjD9DwAfZlWvP81onaxp9KBtAz4GLOayVxsunKhTQ1I5l3WOPSXPC6PLch/lvPEspFFyEck2FZSjtf1q61get5Iqlr8iNfaerYd0HIWFUTXxT+wnfcetSWnPl305yT6mebfUlCbDd0qH4bOUrzeLY7uH1271UexWAmweoRe6SQCfKdIPU1ufrhfohkIZ6YK0LR6PcJx0oXvtBHC6IiLEmW0c00qbvgRRr6esEUSt07playEseUbdyFSCxGdWdQBTQIvNT0hmUlw93+UwOqT9uMAe7cAkWtXJJVU4egAAdQxmf8BAFCwcLGxxGf7AgAAAAAEWVo=|base64 -d|unxz>e.svg;echo \<img src=e.svg height=$1\>>e.htm;firefox e.htm

Answer 10

HTML5, 395

==> Try it online

<canvas id=c><script>_='function e,t,n){c.savtranslate,trotatn?0:.42)}v=docuEleById("c"c=vContex"2d"scalw=(v.width=v.height=promp))/12,w76,1arc(56--114.2,6,66-13,6.-   2,1 11.5)c.clearRec2restor-7mov-71lin6,.5,strokt(   .5--e(0,);1,ment.geteTo(';for(Y in $='  ')with(_.split($[Y]))_=join(pop());eval(_)</script>

The code is compressed using JSCrush.

Here is the uncompressed code :

<canvas id=c>
<script>
v=document.getElementById('c');
c=v.getContext('2d');
function r(){c.rotate(0.42)}
function t(x,y){c.save();c.translate(x,y)}
c.scale(w=(v.width=v.height=prompt())/12,w);
t(7.5,6);
c.arc(0,0,5.5,0,6);
c.stroke();
c.moveTo(-7.5,-1);c.lineTo(6,-1);
c.moveTo(-7.5,1);c.lineTo(6,1);
c.stroke();
c.clearRect(4.2,0,6,6);
t(0,6);r();
c.clearRect(0,-11,3,6.2);
c.restore();
t(-7.5,-0.5);r();
c.clearRect(-1,-2,1,2);
c.restore();
t(-7.5,1.5);r();
c.clearRect(-1,-1.5,1,1.5)
</script>

Answer 11

PostScript, 270

7 7 translate
/l{lineto}def
/o{0 0}def
o 6 44.85 165.52 arc
-7.08 1.5 l
-7.5 .5 l
o 6 175.22 184.74 arc
-7.08 -.5 l
-7.5 -1.5 l
o 6 194.48 309.67 arc
o 5 320 197.46 arcn
1.87 -1.5 l
2.29 -.5 l
o 5 185.74 174.26 arcn
2.7 .5 l
3.12 1.5 l
o 5 162.54 40 arcn
closepath fill

This just defines the outline by appending path elements based on coordinates I calculated with the help of GeoGebra, and then fills the outline.

I saved a few chars by adding shortcuts for lineto (/l{lineto}def) and the origin of the circle (/o{0 0}def).

To specify a different size, add a command of the form height width scale after the first blank line.

When run on its own, this draws the euro sign in the bottom left-hand corner of the page of the default page size. Just save it as anything.ps and view it with a document viewer.

Here is an image of it at the default size, rasterized to a little over 90 pixels per inch:

At 4x size:

You can also download the original for your own viewing pleasure.

Answer 12

PHP (without SVG), 628 597 bytes

Thanks to AsksAnyway for the nice shortcut for functions (e.g. $c = print; $c('Hello world!');).

<?php header('Content-type:image/png');$h=$_GET['h'];$i=imagecreatetruecolor($h*1.1,$h*1.1);$c=imagecolorallocate;$b=$c($i,0,0,0);$w=$c($i,255,255,255);imagefill($i,0,0,$w);$l=$h*.7;$t=$h*.55;$u=$h/12;$e=imagefilledellipse;$e($i,$l,$t,$h,$h,$b);$e($i,$l,$t,$h*5/6,$h*5/6,$w);$f=imagefilledpolygon;$f($i,array($l+$u*5,$t+$u*1.5,$l-$u*7.5,$t+$u*1.5,$l-$u*7.125,$t+$u*0.5,$l+$u*4,$t+$u*.5,$l+$u*4,$t-$u*.5,$l-$u*7.5,$t-$u*.5,$l-$u*7.125,$t-$u*1.5,$l+$u*5,$t-$u*1.5),8,$b);$f($i,array($l+$u*4.24,$t-$u*4.24,$l+$u*1.84,$t+$u*1.5,$l+$u*3.84,$t+$u*3.26,$l+$u*3.84,$t+$u*4.62,$h*2,$t,),5,$w);imagepng($i);

Call file.php?h=200 from your browser in order to see the image

The coordinates are based on measurements performed with GIMP

100 pixels:

200 pixels:

Layers added step by step:

Ungolfed code (with fractions, the golfed code has rounded values)

<?php
header('Content-type: image/png');

$h = $_GET['h'];

$i = imagecreatetruecolor($h * 1.1,$h * 1.1);

$c = imagecolorallocate;

# black
$b = $c($i,0,0,0);
# white
$w = $c($i,255,255,255);

imagefill($i,0,0,$w);

$l = $h * .7; # distance between left and center of the circle
$t = $h * .55; # distance between top and center of the circle

# one "unit", as defined by the specs
$u = $h / 12;

$e = imagefilledellipse;
# disk is black
$e($i, $l, $t, $h, $h, $b);
# inner disk is white
$e($i, $l, $t, $h * (5 / 6), $h * (5 / 6), $w);

$f = imagefilledpolygon;
# draw 2 bars in black
$f($i, array(
# bottom bar
$l + $u * 5, $t + ($u * 1.5), # bottom right
$l-$u * 7.5, $t + ($u * 1.5), # bottom left
$l-$u * 7.125, $t + ($u * 0.5), # top left
$l + $u * 4, $t + ($u * 0.5), # top right
# top bar
$l + $u * 4, $t - ($u * 0.5), # bottom right
$l-$u * 7.5, $t - ($u * 0.5), # bottom left
$l-$u * 7.125, $t - ($u * 1.5), # top left
$l + $u * 5, $t - ($u * 1.5) # top right
), 8, $b);

# hide right parts of bars and circle by drawing white
$f($i, array(
$l + $u * 6 * (212 / 300), $t - ($u * 6 * (212 / 300)), # right of the disk
$l + $u * 6 * (92 / 300), $t + ($u * 6 * (74 / 300)), # left = bottom right of bottom bar
$l + $u * 6 * (191 / 300), $t + ($u * 6 * (163 / 300)), # bottom of the circle
$l + $u * 6 * (191 / 300), $t + ($u * 6 * (231 / 300)), # bottom of the circle too
$h * 2, $t, # some point at the right of the image (outside the image)
), 5, $w);

imagepng($i);

Answer 13

Bash + ImageMagick + linux command-line tools, 460 bytes

base64 -d<<<H4sIADBMaVMAAy1Ru27DMAz8FUJdBVsk9QziLFo8uD/QrUDSOIDTBo1Rt39fUsl0POp0PEr7+88Zfq/L530w87redn2/bVu3cff1fe7JOdeLwsB2Oa7zYDw7A/Ppcp5XJWQO+9v7OsN9/VtOg/m4LMvuRS4ZOA7m1VkseQpBoQZvyXlQQPeA2JpEjVEGURL7EePkLCU3Rqw5Wo4EmLALVgaC9BUrk392OAWt0HUBPHrb+NQq4i5UzigeSU6Zsii5xOYiWLE0BCT1Z89QVKLD2dPEIbdEBasINWIDaiDxG2BjslpBXXTk5CeWFkYa1a2KuS0OMBfJ8RgdKzMr03DRP5Ojy5O8sE2ksdU1g+pcu+SqvILUWddNCBHbCIxvpj/s9ZsO/xXfC57OAQAA|zcat|convert -scale $1 svg:- png:-|xview stdin

This is the same technique as @minitech's answer. But the .svg data comes from here, which is much shorter: http://commons.wikimedia.org/wiki/File:Euro_symbol_black.svg. ImageMagick converts the vector data to .png data at the requested scale and pipes to xview.

Output for ./euro.sh 30:

Output for ./euro.sh 300:

Answer 14

POV-Ray (370 bytes)

I couldn't figure out how to render the same vertical area and preserve the aspect ratio at the same time, so I decided to go for the correct height and its up to the user to render only in 4:3 format

camera{angle 9 location 102*z right x*8 up y*6 look_at 0}
light_source{99*z color 1}
plane{z,0 pigment{color rgb 1}}
#declare b=difference{box{<-5,-.5,1>,<8,.5,1>}box{-2,2 rotate-67*z translate 9.4*x}}
difference{union{torus{5.5,.5 rotate 90*x}object{b translate y}object{b translate -y}}box{<-3.83,-5,-3>,<-7,0,3>}box{<0,7,3>,<-4,-2,-3>rotate 23*z translate-2.5*x}}

run with povray.exe /RENDER euro.pov -w600 -h800

Answer 15

Processing, 232 bytes

Processing doesn't really allow taking in command line arguments since it is so specialized for drawing, but my function takes in the parameter as height to compensate. Coordinates are hard-coded/approximated from the image above, and the entire canvas is scaled based on the input parameter to get drawings of arbitrary sizes.

void E(int h){scale(h/12,h/12);noFill();strokeWeight(1);arc(7.5,6,11,11,0.7,PI*2-0.7,OPEN);noStroke();fill(0);shearX(-PI/6);rect(3.2,4.5,9,1);rect(4.4,6.5,8,1);shearX(PI/6);fill(255);rect(11,6,9,6);triangle(8.75,6,12.25,6,12.25,0);}

Ungolfed + entire program

void setup()
{
  size(575, 500);
}

void draw()
{
  background(255);
  E(height);
  noLoop();
}

void E(int h)
{
  scale(h/12,h/12);
  //Main "C"
  noFill();
  strokeWeight(1);
  arc(7.5,6,11,11,0.7,PI*2-0.7,OPEN);
  //settings for other shapes
  noStroke();
  //the two bars
  fill(0);
  shearX(-PI/6);
  rect(3.2,4.5,9,1);
  rect(4.4,6.5,8,1);
  //bottom cut of "C"
  shearX(PI/6);
  fill(255);
  rect(11,6,9,6);
  //top cut of "C"
  triangle(8.75,6,12.25,6,12.25,0);
}

Output

Answer 16

C (gcc) (MinGW), 277 276 bytes

-1 byte thanks to @ceilingcat

Added -lm compiler flags to TiO for illustrative purposes, but MinGW does not need it.

Outputs a 3-shade PGM file to STDOUT.

q,i,c;main(s,v)char**v;{float u=atoi(v[1])/12.,d,r;q=u*15;for(*v=memset(calloc(q,q+1),2,i=q*q);i--;i[*v]-=d<6&d>5|r>6&r<7|r>8&r<9&&r<7|c<q/2+u*3.83&&u*31.538-s>r*u|r>10&&u*7-s<r*u&&u*9-s<r*u|r<8)r=i/q/u,c=i%q,d=hypot(q/2-c,q/2-r*u)/u,s=2.405*c;printf("P5 %d %d 2 %s",q,q,*v);}

Try it online!