36
4
Given the time in 24 hour format (2359 = 11:59pm) return the angle between the minute and hour hands on a standard clock (on the face plane, so don't just output 0).
Angles are to be returned in the unit of your choice, should be the smallest possible, and should be a positive number (negative angle converted to a positive value), i.e. you will never have an answer greater than 180 degrees or pi radians.
Some examples to check against (in degrees)
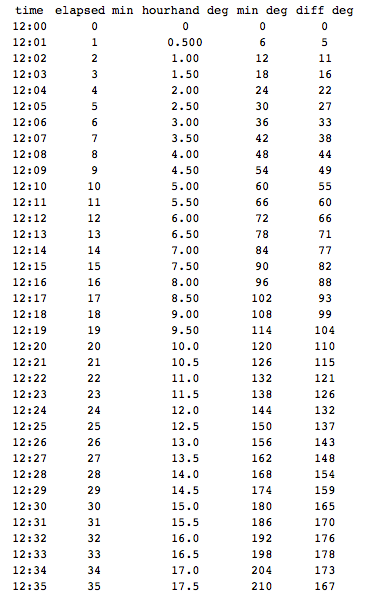
0000=0.00010=55.00020=110.00030=165.00040=140.00050=85.00150=115.00240=160.00725=72.51020=170.01350=115.01725=12.5
Note: There are a few that have rounding errors, I'm not sure how that should be handled; if we should force consistency across all values.
So I'm assuming the input is always a 4 character string? – None – 2011-01-28T04:04:04.317
That is correct @Mike – Dan McGrath – 2011-01-28T04:37:48.217
3You should include some correct input/output examples including "difficult" input like
0001,0633, etc... I notice that many answers actually produce incorrect results. – MtnViewMark – 2011-01-28T06:21:40.437@SimpleCoder: I think a "smallest positive" implies clockwise angle. Counterclockwise would correspond to negative angles. "Smallest" probably means "least multiple of 2*pi". – hallvabo – 2011-01-28T08:51:23.670
It appears that this wasn't originally code-golf. But now that it is, consider revising the accepted answer. – Adám – 2016-01-14T22:56:49.643
1Oh boy, after 5 years my SO notification bar has been going crazy. What a surprising necro, haha. I'll check back in a few days to see if anyone can confirm the APL answer is correct (I'm traveling). I haven't been on this site for ages, but it would sure be nice to be able to mark golfs by language since this has since becoming golfing. – Dan McGrath – 2016-01-14T23:45:44.777
You can download a free APL interpreter from dyalog.com.
– Adám – 2016-01-15T09:16:16.583Why do everybody golf, when it was not supposed to golf? ) – Nakilon – 2011-01-28T18:06:49.223
1@Nakilon: Can't speak for anyone else, but in my case {1} I missed the tagging (need to establish new habits for this place), {2} golfing is why I came here, and {3} it's kind of simple for anything else, isn't it? – dmckee --- ex-moderator kitten – 2011-01-28T18:44:26.667
A few of the example answers are incorrect and the question is poorly worded ("positive angle only" for instance). I've corrected the examples, clarified the answer, and provided some more examples to highlight possible errors. – None – 2011-01-29T02:01:55.847
2The clockwise angle, or the smallest of the two? – Chris Laplante – 2011-01-27T22:18:28.000
1@SimpleCoder: Smallest, as the question says. – Chris Jester-Young – 2011-01-27T22:21:03.007
00:10will be0010or010? – Nakilon – 2011-01-28T00:04:22.603It will be
0010in 24 hour time @Nakilon – Dan McGrath – 2011-01-28T00:22:03.387