Generate Newton fractals

Question

You all know the Newton method to approximate the roots of a function, don't you? My goal in this task is to introduce you into an interesting aspect of this algorithm.

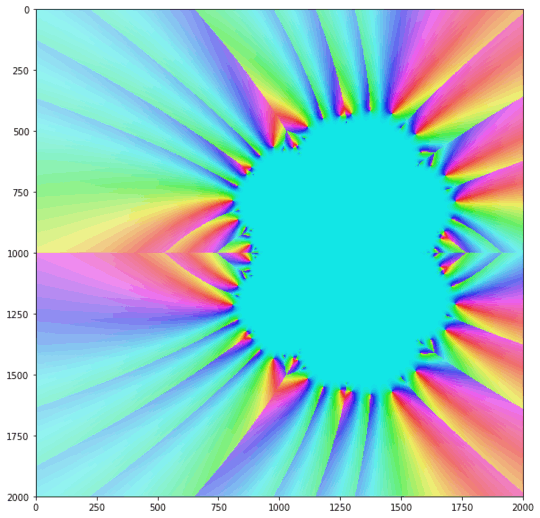
Newton's algorithm converges only for certain, but most of all complex input values. If you picture the convergence of the method for all input values over the complex plane, you usually get a beautiful fractal like this:

Image from Wikimedia commons

Specifications

The goal of this task is, to generate such fractals. This means, that you get a polynomial as the input and have to print out the corresponding fractal as an image in a format of your choice as the output.

Input

The input is a whitespace-separated list of complex numbers. They are written down in the style <Real part><iImaginary part>, like this number: 5.32i3.05. You may assume, that the input number has no more than 4 decimal places and is smaller than 1000. The first of them must not be zero. For example, this could be an input to your program:

1 -2i7.5 23.0004i-3.8 i12 0 5.1233i0.1

The numbers are interpreted as the coefficients of a polynomial, beginning with the highest power. Throughout the rest of this specification, the input polynomial is called P. The above input is equal to this polynomial:

f(x) = x5 + (-2 + 7.5i)x4 + (23.0004 - 3.8i)x3 + 12ix2 + 5.1233 + 0.1i

The input may come to you either from stdin, from an argument passed to the program or from a prompt displayed to your program. You may assume, that the input does not contain any leading or trailing whitespace characters.

Rendering

You have to render the fractal in the following way:

• Choose as many colors as roots of P plus an extra color for divergence
• For each number in the visible plane, determine whether the method converges and if yes to which root. Color the point according to the result.
• Do not print rulers or other fancy things
• Print a black point at the points, that are the polynomials roots for orientation. You may print up to four pixels around each root.
• Find a way to choose the visible plane in a way, that all roots are distinguishable and spread widely across it, if possible. Although a perfect placement of the output frame is not required, I reserve the right to refuse to accept an answer that chooses the frame in an unacceptable way, eg. always at the same coordinates, all roots are in one point, etc.
• The output image should have a size of 1024*1024 pixels.
• Rendering time is 10 minutes maximum
• Using single precision floating-point values is enough

Output

The output should be a raster graphics image in a file format of your choice, readable by standard software for a brand X operating system. If you want to use a rare format, consider adding a link to a website where one can download a viewer for it.

Output the file to stdout. If your language does not support putting something to stdout or if you find this option less convenient, find another way. In any way, it must be possible to save the generated image.

Restrictions

• No image processing libraries
• No fractal generating libraries
• The shortest code wins

Extensions

If you like this task, you could try to color the points according to the speed of convergence or some other criteria. I'd like to see some interesting results.

Answer 1

Python, 827 777 chars

import re,random
N=1024
M=N*N
R=range
P=map(lambda x:eval(re.sub('i','+',x)+'j'if 'i'in x else x),raw_input().split())[::-1]
Q=[i*P[i]for i in R(len(P))][1:]
E=lambda p,x:sum(x**k*p[k]for k in R(len(p)))
def Z(x):
 for j in R(99):
  f=E(P,x);g=E(Q,x)
  if abs(f)<1e-9:return x,1
  if abs(x)>1e5or g==0:break
  x-=f/g
 return x,0
T=[]
a=9e9
b=-a
for i in R(999):
 x,f=Z((random.randrange(-9999,9999)+1j*random.randrange(-9999,9999))/99)
 if f:a=min(a,x.real,x.imag);b=max(b,x.real,x.imag);T+=[x]
s=b-a
a,b=a-s/2,b+s/2
s=b-a
C=[[255]*3]*M
H=lambda x,k:int(x.real*k)+87*int(x.imag*k)&255
for i in R(M):
 x,f=Z(a+i%N*s/N+(a+i/N*s/N)*1j)
 if f:C[i]=H(x,99),H(x,57),H(x,76)
for r in T:C[N*int(N*(r.imag-a)/s)+int(N*(r.real-a)/s)]=0,0,0
print'P3',N,N,255
for c in C:print'%d %d %d'%c

Finds display bounds (and roots) by finding convergence points for a bunch of random samples. It then draws the graph by computing the convergence points for each starting point and using a hash function to get randomish colors for each convergence point. Look very closely and you can see the roots marked.

Here's the result for the example polynomial.

Answer 2

Java, 1093 1058 1099 1077 chars

public class F{double r,i,a,b;F(double R,double I){r=R;i=I;}F a(F c){return
new F(r+c.r,i+c.i);}F m(F c){return new F(r*c.r-i*c.i,r*c.i+i*c.r);}F
r(){a=r*r+i*i;return new F(-r/a,i/a);}double l(F c){a=r-c.r;b=i-c.i;return
Math.sqrt(a*a+b*b);}public static void main(String[]a){int
n=a.length,i=0,j,x,K=1024,r[]=new int[n];String o="P3\n"+K+" "+K+"\n255 ",s[];F z=new
F(0,0),P[]=new F[n],R[]=new F[n],c,d,e,p,q;for(;i<n;)P[i]=new
F((s=a[i++].split("i"))[0].isEmpty()?0:Float.parseFloat(s[0]),s.length==1?0:Float.parseFloat(s[1]));double
B=Math.pow(P[n-1].m(P[0].r()).l(z)/2,1./n),b,S;for(i=1;i<n;){b=Math.pow(P[i].m(P[i-1].r()).l(z),1./i++);B=b>B?b:B;}S=6*B/K;for(x=0;x<K*K;){e=d=c=new
F(x%K*S-3*B,x++/K*S-3*B);for(j=51;j-->1;){p=P[0];q=p.m(new
F(n-1,0));for(i=1;i<n;){if(i<n-1)q=q.m(c).a(P[i].m(new
F(n-1-i,0)));p=p.m(c).a(P[i++]);}c=c.a(d=q.r().m(p));if(d.l(z)<S/2)break;}i=j>0?0:n;for(;i<n;i++){if(R[i]==null)R[i]=c;if(R[i].l(c)<S)break;}i=java.awt.Color.HSBtoRGB(i*1f/n,j<1||e.l(c)<S&&r[i]++<1?0:1,j*.02f);for(j=0;j++<3;){o+=(i&255)+" ";i>>=8;}System.out.println(o);o="";}}}

Input is command-line arguments - e.g. run java F 1 0 0 -1. Output is to stdout in PPM format (ASCII pixmap).

The scale is chosen using the Fujiwara bound on the absolute value of the complex roots of a polynomial; I then multiply that bound by 1.5. I do adjust brightness by convergence rate, so the roots will be in the brightest patches. Therefore it's logical to use white rather than black to mark the approximate locations of the roots (which is costing me 41 chars for something which can't even be done "correctly". If I label all points which converge to within 0.5 pixels of themselves then some roots come out unlabelled; if I label all points which converge to within 0.6 pixels of themselves then some roots come out labelled over more than one pixel; so for each root I label the first point encountered to converge to within 1 pixel of itself).

Image for the example polynomial (converted to png with the GIMP):

Answer 3

Python, 633 bytes

import numpy as np
import matplotlib.pyplot as plt
from colorsys import hls_to_rgb
def f(z):
    return (z**4 - 1)
def df(z):
    return (4*z**3) 
def cz(z):
    r = np.abs(z)
    arg = np.angle(z)   
    h = (arg + np.pi)  / (3 * np.pi)
    l = 1.0 - 1.0/(1.0 + r**0.1)
    s = 0.8 
    c = np.vectorize(hls_to_rgb) (h,l,s)
    c = np.array(c)
    c = c.swapaxes(0,2) 
    return c    
x, y = np.ogrid[-1.5:1.5:2001j, -1.5:1.5:2001j]
z = x + 1j*y    
for i in range(10):
    z -= (f(z) / df(z))
zz = z
zz[np.isnan(zz)]=0
zz=cz(zz)
plt.figure()
plt.imshow(zz, interpolation='nearest')
plt.axis('off')
plt.savefig('plots/nf.svg')
plt.close()

After Speed Ups and Beautification (756 bytes)

import numpy as np
from numba import jit
import matplotlib.pyplot as plt
from colorsys import hls_to_rgb 

@jit(nopython=True, parallel=True, nogil=True)
def f(z):
    return (z**4 - 1)   

@jit(nopython=True, parallel=True, nogil=True)
def df(z):
    return (4*z**3) 

def cz(z):
    r = np.abs(z)
    arg = np.angle(z)   

    h = (arg + np.pi)  / (3 * np.pi)
    l = 1.0 - 1.0/(1.0 + r**0.1)
    s = 0.8 

    c = np.vectorize(hls_to_rgb) (h,l,s)
    c = np.array(c)
    c = c.swapaxes(0,2) 
    return c    

x, y = np.ogrid[-1.5:1.5:2001j, -1.5:1.5:2001j]
z = x + 1j*y    

for i in range(10):
    z -= (f(z) / df(z))

zz = z
zz[np.isnan(zz)]=0
zz=cz(zz)
plt.figure()
plt.imshow(zz, interpolation='nearest')
plt.axis('off')
plt.savefig('plots/nf.svg')
plt.close()

The plot below is for Newton Fractal of log(z) function.