Regex (ECMAScript+(?*)), 1169 929 887 853 849 bytes
Regex was never designed to do mathematics. It has no concept of arithmetic. However, when input is taken in the form of bijective unary, as a sequence of identical characters in which the length represents a natural number, it is possible to do a wide range of operations, building up from the simple primitives available, which basically amount to addition, comparison, multiplication by a constant, and modulo. Everything must fit inside the input; it isn't possible to directly operate on numbers larger than that.
In ECMAScript regex, it's especially difficult (and therefore interesting) to do even some of the simplest of operations, because of the limitation that all backrefs captured in a loop are reset to empty at the beginning of each iteration – which makes it impossible to count anything directly. It's nevertheless possible to match prime numbers, powers of N, Nth powers, arbitrary multiplication and exponentiation, Fibonacci numbers, factorial numbers, abundant numbers, and more, much of which is demonstrated in my other answers.
One of the operations that turns out to be far more verbose than the rest is to "calculate an irrational number". I initially discussed this with teukon back in 2014. The only known way to do this is to emulate operations on numbers larger than the input, and probably the simplest way to do this is by working in a number base chosen based on what can fit into the input.
It wasn't until late 2018 that I finally set about to implementing the theory I had sketched in 2014. Implementing it involved adapting the multiplication algorithm to work with factors of 0, which turned out to golf rather elegantly. (The underlying multiplication algorithm is explained in this post.) The basic algorithm is this:
For input \$N\$, we want to calculate \$M=\lfloor{N\over\sqrt2}\rfloor\$. So we want the largest \$M\$ such that \$2M^2\le N^2\$.
If we take the "number base" to be \$k=\lceil\sqrt N\rceil\$ or \$\lfloor\sqrt N\rfloor\!+\!1\$, all multiplication operations \$m\cdot n\$ on \$0\leq m,n<k\$ are guaranteed to fit in the available space.
So if \$N=A k+B\$, where \$0\leq A,B\lt k\$, we can calculate \$N^2\$:
$$N^2=(A k+B)^2=A^2 k^2+2 A B k+B^2$$
We must then do division, modulo, and carry to bring \$A^2\$, \$2 A B\$, and \$B^2\$ back into the range of a base \$k\$ "digit". A similar operation is then done to calculate \$2 M^2\$ iterated over the decreasing consecutive possible values of \$M\$, using digit-by-digit comparison to test for \$2M^2\le N^2\$, until the first \$M\$ is found that passes the test.
So while the basic concept is simple enough, it adds up to a lot of calculations, and the regex is huge! And this is probably the simplest calculation of an irrational number that can be done in ECMAScript regex. (It is still unknown whether it's possible to calculate a transcendental number to arbitrary precision in regex.)
This regex uses molecular lookahead, a.k.a. non-atomic lookahead, represented as (?*...). Without this feature, it would be much harder (or at least much more verbose) to implement.
Note that there is one departure from pure code golf in this version of the regex. I chose to use \$k=\lceil\sqrt N\rceil\$ because it has the very neat property of making the calculations fit perfectly into \$N\$ if \$N\$ is a perfect square, whereas \$k=\lfloor\sqrt N\rfloor\!+\!1\$ is basically chaotic for all inputs. They both yield the same final outputs, but the former is just cleaner. This only involved increasing the total length of the regex by 8 bytes, so I figured it was worth it. This change is in the git version history.
(?=(x(x*))(x)*(?=\1*$)\2+$)(?=(x(\2\3))+(x?(x*)))(?=\6(x(x*))(?=\8*$)\5\9*$)(?=.*(?=(?=\6*$)\6\7+$)(x*?)(?=\4*$)(x?(x*))(?=\11*$)((?=\5+$)\5\12*$|$\11))(?=.*(?=(?=\6*$)(?=\8*$)(?=\6\9+$)\8\7+$|$\6)(x*?)(?=\4*$)(x?(x*))(?=\15*$)((?=\5+$)\5\16*$|$\15))(?=.*(?=\14\14\11$)(x*?)(?=\4*$)(x?(x*))(?=\19*$)((?=\5+$)\5\20*$|$\19))(?*.*?(?=((?=\4*(x?(x*)))\23(x(x*))(?=\25*$)\5\26*$)))(?=.*(?=\25*$)(\25\26+$))(?=.*(?=(?=\23*$)\23\24+$)(x*?)(?=\4*$)(x?(x*))(?=\29*$)((?=\5+$)\5\30*$|$\29))(?=.*(?=(?=\23*$)(?=\25*$)(?=\23\26+$)\25\24+$|$\23)(x*?)(?=\4*$)(x?(x*))(?=\33*$)((?=\5+$)\5\34*$|$\33))(?=.*(?=\32\32\29$)(x*?)(?=\4*$)(x?(x*))(?=\37*$)((?=\5+$)\5\38*$|$\37))(?=.*(?=\28\28)(?=\4*(x*))(\5(x)|))(?=.*(?=\36\36\42)(?=\4*(x*))(\5(x)|))(?=(?=(.*)\15\15\19(?=\8*$)\8\9+$)\46(x+|(?=.*(?!\18)\43|(?!.*(?!\40)\10).*(?=\18$)\43$))(\27\33\33\37){2}\45$)\22|x\B|
Try it on repl.it
This regex is on GitHub with a full version history.
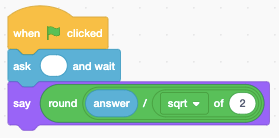
# Giving an input number N in the domain ^x*$, this regex returns floor(N / sqrt(2))
(?=
(x(x*)) # \1 = will be the square root of the main number, rounded down; \2 = \1 - 1
(x)*(?=\1*$) # \3 = tool to round up instead of down
\2+$
)
# Step 1: Calculate N*N in base ceil(sqrt(N))
(?=(x(\2\3))+(x?(x*))) # \4 = \1 + \3 = ceil(sqrt(N)), the number base to work in; \5 = \4-1; \6 = N % \4; \7 = \6-1, or 0 if \6==0
(?=
\6
(x(x*)) # \8 = floor(N / \4); \9 = \8-1
(?=\8*$) # we can skip the test for divisibility by \5 because it's guaranteed that \5 <= \8
\5\9*$
)
(?=
.*
(?=
(?=\6*$) # tail = \6 * \6
\6\7+$
)
(x*?)(?=\4*$) # \10 = (\6 * \6) % \4, the base-\4 digit in place 0 of the result for N*N
(x?(x*)) # \11 = floor((\6 * \6) / \4); \12 = \11-1, or 0 if \11==0
(?=\11*$)
(
(?=\5+$)
\5\12*$
|
$\11 # must make a special case for \11==0, because \5 is nonzero
)
)
(?=
.*
(?=
(?=\6*$) # tail = \6 * \8; must do symmetric multiplication, because \6 is occasionally 1 larger than \8
(?=\8*$)
(?=\6\9+$)
\8\7+$
|
$\6 # must make a special case for \6==0, because \8 might not be 0
)
(x*?)(?=\4*$) # \14 = (\6 * \8) % \4
(x?(x*)) # \15 = floor((\6 * \8) / \4); \16 = \15-1, or 0 if \15==0
(?=\15*$)
(
(?=\5+$)
\5\16*$
|
$\15 # must make a special case for \15==0, because \5 is nonzero
)
)
(?=
.*(?=\14\14\11$) # tail = 2 * \14 + \11
(x*?)(?=\4*$) # \18 = (2 * \14 + \11) % \4, the base-\4 digit in place 1 of the result for N*N
(x?(x*)) # \19 = floor((2 * \14 + \11) / \4); \20 = \19-1, or 0 if \19==0
(?=\19*$)
(
(?=\5+$)
\5\20*$
|
$\19 # must make a special case for \19==0, because \5 is nonzero
)
) # {\8*\8 + 2*\15 + \19} = the base-\4 digit in place 2 of the result for N*N, which is allowed to exceed \4 and will always do so;
# Note that it will be equal to N iff N is a perfect square, because of the choice of number base.
# Step 2: Find the largest M such that 2*M*M is not greater than N*N
# Step 2a: Calculate M*M in base \4
(?*
.*? # Determine value of M with backtracking, starting with largest values first
(?=
( # \22 = M
(?=\4*(x?(x*)))\23 # \23 = M % \4; \24 = \23-1, or 0 if \23==0
(x(x*)) # \25 = floor(M / \4); \26 = \25-1
(?=\25*$) # we can skip the test for divisibility by \5, but I'm not sure why; TODO: figure out why this is
\5\26*$
)
)
)
(?=
.*
(?=\25*$)
(\25\26+$) # \27 = \25 * \25
)
(?=
.*
(?=
(?=\23*$) # tail = \23 * \23
\23\24+$
)
(x*?)(?=\4*$) # \28 = (\23 * \23) % \4, the base-\4 digit in place 0 of the result for M*M
(x?(x*)) # \29 = floor((\23 * \23) / \4); \30 = \29-1, or 0 if \29==0
(?=\29*$)
(
(?=\5+$)
\5\30*$
|
$\29 # must make a special case for \29==0, because \5 is nonzero
)
)
(?=
.*
(?=
(?=\23*$) # tail = \23 * \25; must do symmetric multiplication, because \23 is occasionally 1 larger than \25
(?=\25*$)
(?=\23\26+$)
\25\24+$
|
$\23 # must make a special case for \23==0, because \25 might not be 0
)
(x*?)(?=\4*$) # \32 = (\23 * \25) % \4
(x?(x*)) # \33 = floor((\23 * \25) / \4); \34 = \33-1, or 0 if \33==0
(?=\33*$)
(
(?=\5+$)
\5\34*$
|
$\33 # must make a special case for \33==0, because \5 is nonzero
)
)
(?=
.*(?=\32\32\29$) # tail = 2 * \32 + \29
(x*?)(?=\4*$) # \36 = (2 * \32 + \29) % \4, the base-\4 digit in place 1 of the result for M*M
(x?(x*)) # \37 = floor((2 * \32 + \29) / \4); \38 = \37-1, or 0 if \37==0
(?=\37*$)
(
(?=\5+$)
\5\38*$
|
$\37 # must make a special case for \37==0, because \5 is nonzero
)
) # {\27 + 2*\33 + \37} = the base-\4 digit in place 2 of the result for M*M, which is allowed to exceed \4 and will always do so
# Step 2b: Calculate 2*M*M in base \4
(?=
.*
(?=\28\28) # tail = 2*\28
(?=\4*(x*)) # \40 = (2*\28) % \4, the base-\4 digit in place 0 of the result for 2*M*M
(\5(x)|) # \42 = floor((2*\28) / \4) == +1 carry if {2*\28} does not fit in a base \4 digit
)
(?=
.*
(?=\36\36\42) # tail = 2*\36 + \42
(?=\4*(x*)) # \43 = (2*\36 + \42) % \4, the base-\4 digit in place 1 of the result for 2*M*M
(\5(x)|) # \45 = floor((2*\36 + \42) / \4) == +1 carry if {2*\36 + \42} does not fit in a base \4 digit
) # 2*(\27 + 2*\33 + \37) + \45 = the base-\4 digit in place 2 of the result for 2*M*M, which is allowed to exceed \4 and will always do so
# Step 2c: Require that 2*M*M <= N*N
(?=
(?=
(.*) # \46
\15\15\19
(?=\8*$) # tail = \8 * \8
\8\9+$
)
\46 # tail = {\8*\8 + 2*\15 + \19}; we can do this unconditionally because our digits in place 2 are always greater than those in places 0..1
(
x+
|
(?=
.*(?!\18)\43 # \43 < \18
|
(?!.*(?!\40)\10) # \40 <= \10
.*(?=\18$)\43$ # \43 == \18
)
)
(\27\33\33\37){2}\45$ # 2*(\27 + 2*\33 + \37) + \45
)
\22
|x\B| # handle inputs in the domain ^x{0,2}$
Regex (ECMAScript 2018), 861 bytes
This is a direct port of the 849 byte molecular lookahead version, using variable length lookbehind.
(?=(x(x*))(x)*(?=\1*$)\2+$)(?=(x(\2\3))+(x?(x*)))(?=\6(x(x*))(?=\8*$)\5\9*$)(?=.*(?=(?=\6*$)\6\7+$)(x*?)(?=\4*$)(x?(x*))(?=\11*$)((?=\5+$)\5\12*$|$\11))(?=.*(?=(?=\6*$)(?=\8*$)(?=\6\9+$)\8\7+$|$\6)(x*?)(?=\4*$)(x?(x*))(?=\15*$)((?=\5+$)\5\16*$|$\15))(?=.*(?=\14\14\11$)(x*?)(?=\4*$)(x?(x*))(?=\19*$)((?=\5+$)\5\20*$|$\19))(?=.*?(?=((?=\4*(x?(x*)))\23(x(x*))(?=\25*$)\5\26*$))(?<=(?=(?=.*(?=\25*$)(\25\26+$))(?=.*(?=(?=\23*$)\23\24+$)(x*?)(?=\4*$)(x?(x*))(?=\29*$)((?=\5+$)\5\30*$|$\29))(?=.*(?=(?=\23*$)(?=\25*$)(?=\23\26+$)\25\24+$|$\23)(x*?)(?=\4*$)(x?(x*))(?=\33*$)((?=\5+$)\5\34*$|$\33))(?=.*(?=\32\32\29$)(x*?)(?=\4*$)(x?(x*))(?=\37*$)((?=\5+$)\5\38*$|$\37))(?=.*(?=\28\28)(?=\4*(x*))(\5(x)|))(?=.*(?=\36\36\42)(?=\4*(x*))(\5(x)|))(?=(?=(.*)\15\15\19(?=\8*$)\8\9+$)\46(x+|(?=.*(?!\18)\43|(?!.*(?!\40)\10).*(?=\18$)\43$))(\27\33\33\37){2}\45$))^.*))\22|x\B|
Try it online!
This regex is on GitHub.
# Giving an input number N in the domain ^x*$, this regex returns floor(N / sqrt(2))
(?=
(x(x*)) # \1 = will be the square root of the main number, rounded down; \2 = \1 - 1
(x)*(?=\1*$) # \3 = tool to round up instead of down
\2+$
)
# Step 1: Calculate N*N in base ceil(sqrt(N))
(?=(x(\2\3))+(x?(x*))) # \4 = \1 + \3 = ceil(sqrt(N)), the number base to work in; \5 = \4-1; \6 = N % \4; \7 = \6-1, or 0 if \6==0
(?=
\6
(x(x*)) # \8 = floor(N / \4); \9 = \8-1
(?=\8*$) # we can skip the test for divisibility by \5 because it's guaranteed that \5 <= \8
\5\9*$
)
(?=
.*
(?=
(?=\6*$) # tail = \6 * \6
\6\7+$
)
(x*?)(?=\4*$) # \10 = (\6 * \6) % \4, the base-\4 digit in place 0 of the result for N*N
(x?(x*)) # \11 = floor((\6 * \6) / \4); \12 = \11-1, or 0 if \11==0
(?=\11*$)
(
(?=\5+$)
\5\12*$
|
$\11 # must make a special case for \11==0, because \5 is nonzero
)
)
(?=
.*
(?=
(?=\6*$) # tail = \6 * \8; must do symmetric multiplication, because \6 is occasionally 1 larger than \8
(?=\8*$)
(?=\6\9+$)
\8\7+$
|
$\6 # must make a special case for \6==0, because \8 might not be 0
)
(x*?)(?=\4*$) # \14 = (\6 * \8) % \4
(x?(x*)) # \15 = floor((\6 * \8) / \4); \16 = \15-1, or 0 if \15==0
(?=\15*$)
(
(?=\5+$)
\5\16*$
|
$\15 # must make a special case for \15==0, because \5 is nonzero
)
)
(?=
.*(?=\14\14\11$) # tail = 2 * \14 + \11
(x*?)(?=\4*$) # \18 = (2 * \14 + \11) % \4, the base-\4 digit in place 1 of the result for N*N
(x?(x*)) # \19 = floor((2 * \14 + \11) / \4); \20 = \19-1, or 0 if \19==0
(?=\19*$)
(
(?=\5+$)
\5\20*$
|
$\19 # must make a special case for \19==0, because \5 is nonzero
)
) # {\8*\8 + 2*\15 + \19} = the base-\4 digit in place 2 of the result for N*N, which is allowed to exceed \4 and will always do so;
# Note that it will be equal to N iff N is a perfect square, because of the choice of number base.
# Step 2: Find the largest M such that 2*M*M is not greater than N*N
# Step 2a: Calculate M*M in base \4
(?=
.*? # Determine value of M with backtracking, starting with largest values first
(?=
( # \22 = M
(?=\4*(x?(x*)))\23 # \23 = M % \4; \24 = \23-1, or 0 if \23==0
(x(x*)) # \25 = floor(M / \4); \26 = \25-1
(?=\25*$) # we can skip the test for divisibility by \5, but I'm not sure why; TODO: figure out why this is
\5\26*$
)
)
(?<= # emulate molecular lookahead for the above expressions
(?=
(?=
.*
(?=\25*$)
(\25\26+$) # \27 = \25 * \25
)
(?=
.*
(?=
(?=\23*$) # tail = \23 * \23
\23\24+$
)
(x*?)(?=\4*$) # \28 = (\23 * \23) % \4, the base-\4 digit in place 0 of the result for M*M
(x?(x*)) # \29 = floor((\23 * \23) / \4); \30 = \29-1, or 0 if \29==0
(?=\29*$)
(
(?=\5+$)
\5\30*$
|
$\29 # must make a special case for \29==0, because \5 is nonzero
)
)
(?=
.*
(?=
(?=\23*$) # tail = \23 * \25; must do symmetric multiplication, because \23 is occasionally 1 larger than \25
(?=\25*$)
(?=\23\26+$)
\25\24+$
|
$\23 # must make a special case for \23==0, because \25 might not be 0
)
(x*?)(?=\4*$) # \32 = (\23 * \25) % \4
(x?(x*)) # \33 = floor((\23 * \25) / \4); \34 = \33-1, or 0 if \33==0
(?=\33*$)
(
(?=\5+$)
\5\34*$
|
$\33 # must make a special case for \33==0, because \5 is nonzero
)
)
(?=
.*(?=\32\32\29$) # tail = 2 * \32 + \29
(x*?)(?=\4*$) # \36 = (2 * \32 + \29) % \4, the base-\4 digit in place 1 of the result for M*M
(x?(x*)) # \37 = floor((2 * \32 + \29) / \4); \38 = \37-1, or 0 if \37==0
(?=\37*$)
(
(?=\5+$)
\5\38*$
|
$\37 # must make a special case for \37==0, because \5 is nonzero
)
) # {\27 + 2*\33 + \37} = the base-\4 digit in place 2 of the result for M*M, which is allowed to exceed \4 and will always do so
# Step 2b: Calculate 2*M*M in base \4
(?=
.*
(?=\28\28) # tail = 2*\28
(?=\4*(x*)) # \40 = (2*\28) % \4, the base-\4 digit in place 0 of the result for 2*M*M
(\5(x)|) # \42 = floor((2*\28) / \4) == +1 carry if {2*\28} does not fit in a base \4 digit
)
(?=
.*
(?=\36\36\42) # tail = 2*\36 + \42
(?=\4*(x*)) # \43 = (2*\36 + \42) % \4, the base-\4 digit in place 1 of the result for 2*M*M
(\5(x)|) # \45 = floor((2*\36 + \42) / \4) == +1 carry if {2*\36 + \42} does not fit in a base \4 digit
) # 2*(\27 + 2*\33 + \37) + \45 = the base-\4 digit in place 2 of the result for 2*M*M, which is allowed to exceed \4 and will always do so
# Step 2c: Require that 2*M*M <= N*N
(?=
(?=
(.*) # \46
\15\15\19
(?=\8*$) # tail = \8 * \8
\8\9+$
)
\46 # tail = {\8*\8 + 2*\15 + \19}; we can do this unconditionally because our digits in place 2 are always greater than those in places 0..1
(
x+
|
(?=
.*(?!\18)\43 # \43 < \18
|
(?!.*(?!\40)\10) # \40 <= \10
.*(?=\18$)\43$ # \43 == \18
)
)
(\27\33\33\37){2}\45$ # 2*(\27 + 2*\33 + \37) + \45
)
)
^.* # emulate molecular lookahead
)
)
\22
|x\B| # handle inputs in the domain ^x{0,2}$
Regex (ECMAScript)
I have not yet ported this algorithm to basic ECMAScript. One way to do it would be to use \$k=\lceil\sqrt[\uproot{1}3]N\rceil\$ as the number base, and calculate:
$$N^2=(A k^2+B k+C)^2=A^2 k^4 + 2 A B k^3 + (2 A C + B^2)k^2 + 2 B C k + C^2$$
Another way would be to stick with \$k=\lceil\sqrt N\rceil\$, capture \$M\$ encoded into two or more backrefs, and emulate the existing calculations within the smaller available space. I'm not sure which way would be more concise. Either way, I expect the regex would roughly double in length.
9
Just in case someone is tempted to use Brainbool or something similar, I'll just leave a link to the appropriate loophole here.
– FryAmTheEggman – 2020-01-24T06:26:28.8736Shifting half a bit requires more than bitwise insight to solve. – None – 2020-01-24T10:29:38.570
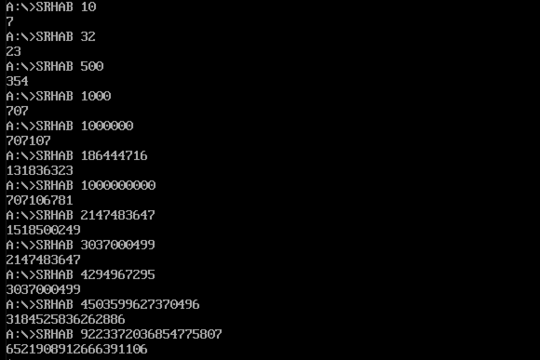
4Suggested test case: 9223372036854775807 – 640KB – 2020-01-24T22:18:45.567