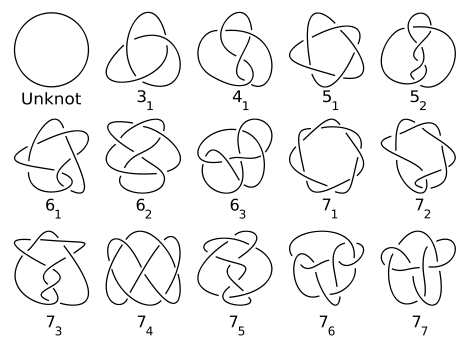Haskell, 249 246 bytes
(i#x)a=[head$[x|j==i]++[s]|(j,s)<-zip[0..]a]
(s%i)[]=i<2&&elem 2(concat s)
(s%i)((l,a):b)|l,[]<-s!!a=or[(a#[i,x]$s)%x$b|x<-[1..3]]|[]<-s!!a=(a#[i]$s)%i$b|[x]<-s!!a,x==i=s%i$b|[x]<-s!!a=s%(6-i-x)$b|u<-s!!a=mod(sum$i:u)3<1&&(s%i)b
f x=(x>>[[]])%1$x
Try it online!
Takes input as a Gauss Code, ([(Bool, Int)]) where False represents crossing over and True represents under
Explanation
This algorithm works by stepping though each intersection and trying to resolve the colors of that intersection. It keeps track of what color the strand is and branches if multiple colors are possible at a given point.
The function that we build to do this is called r. It takes, 3 arguments:
- The Gauss Code of the knot we are working on (which it will consume in order)
- A list of "intersections" and what colors we have already filled in
- The color of the strand where we are currently processing.
Our intersections are represented as a list of colors (Int), which we know to be at that intersection. There are three possible states for this:
- It is empty, meaning we have not visited this intersection yet.
- It has one element, meaning we visited the intersection going over.
- It has two elements (possibly equal), meaning we visited the intersection going under.
We can't have 3 elements because when we visit an intersection the second time we don't have to add the third element since we are never coming back. Since we don't have to and this is code-golf, we don't.
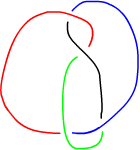
At each step of the way we can use a very simple case analysis to determine how to branch. Here is a diagram showing each case and the possible outputs (no possible outputs is a contradiction and return False if we reach it). Incoming color and location are indicated with the small arrow.
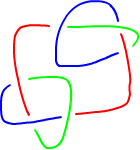
Here are some sample paths of execution on the granny knot and the figure 8 knot as shown in the question. I skip over steps where we went over a unvisited intersection, since they are quite trivial and the diagrams are quite large even without them.
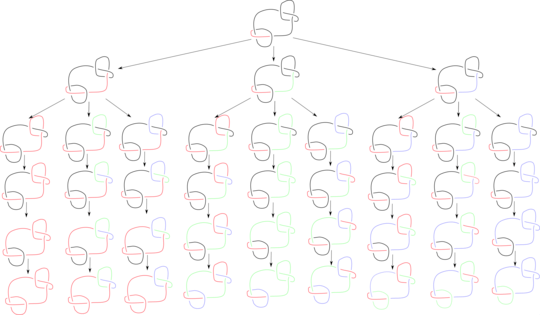
Since Haskell is lazy we only ever evaluate two of these paths, the left-most path, and when that fails because the result doesn't have two colors we evaluate the second left-most. Since that one passes we exit without further evaluation.
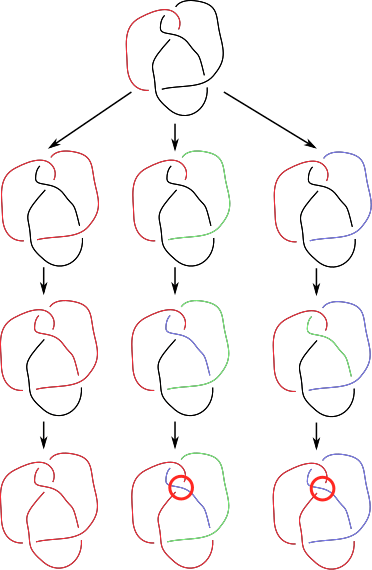
Here the only branch that does not encounter an error colors everything the same way.
Here is my code ungolfed a bit and commented. I will expand this a little bit shortly.
-- Update an element of a list
q i x a=[head$[x|j==i]++[s]|(j,s)<-zip[0..]a]
-- Perform the algorithm
-- Iterates through the intersections in order
-- It records colors at each intersection and searches for a contradiction
r[]s i=i<2&&elem 2(concat s)
r((l,a):b)s i
-- If we reach a new intersection passing under
-- Branch on the three possible colors
-- label the intersection with the incoming and outgoing colors
|l,[]<-s!!a=or[r b(q a[i,x]s)x|x<-[1..3]]
-- If we reach a new intersection passing over
-- label the intersection with the incoming color
|[]<-s!!a=r b(q a[i]s)i
-- If we reach an intersection going under where the over strand is the same color as the incoming
-- The outgoing strand is the same color
|[x]<-s!!a,x==i=r b s i
-- If we reach an intersection going under where the over strand is different from the incoming
-- The outgoing strand is the third color
|[x]<-s!!a=r b s(6-i-x)
-- If we reach an intersection going under
-- Check that the three strands have either all the same or all different colors
-- Since we use 1,2 and 3 for the colors this is the same as checking if their sum is divisible by 3
|u<-s!!a=mod(sum$i:u)3<1&&r b s i
f x=r x(x>>[[]])1