L tromino tiling

Question

Inspired by this challenge from puzzling.SE.

Polyominoes are fun - you can fill all sorts of shapes with them. But as soon as you have limits on what polyominoes you can use, you sadly start running into shapes you can't fill.

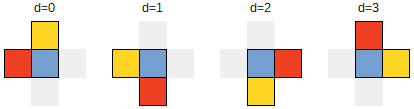
Today we'll be looking at the L tromino - a shape made up of three conjoined squares, in such a way that all three squares are of the same size, and there is a corner which they all share. It looks like this:

Now, given a shape made out of equal-size squares as input, the challenge is to find out whether that shape can be filled using only non-overlapping L-trominoes that are placed entirely within the input figure. You may have any number of these trominoes, and you may rotate each of them by any integer multiple of 90°.

Rules

• The challenge is to make a program or function.
• Your program will recieve as input a two-dimensional list of values.
• Each entry in the list will contain one of two consistent values of your choice - one to signify that a square should be filled, and the other to signify that it shouldn't.
• You may assume there will be at least one row and at least one column, and that every row and every column will contain at least one cell that needs to be filled. You may also either assume that all rows have been padded to be of equal length, or that they contain nothing after their last filled cell - you may also independently assume either of those for the columns. That is to say, with 1 as squares you need to fill, and 0 as squares you need to not fill, you only need to be able to handle one of these four inputs (if given one of the others, your program's behaviour is undefined):

1 1 0
1 1 1
0 1 0

1 1
1 1 1
0 1

1 1 0
1 1 1
  1

1 1
1 1 1
  1

• To fill some square, you must also fill two other squares. Exactly two of the three squares filled must be diagonally adjacent to (sharing a corner with) eachothers, and they must both be orthogonally adjacent to (sharing a side with) the third.
• You may assume the input shape is contiguous.
• You may assume the input's dimensions will be no greater than 5x5.
• You may not assume the number of rows and the number of columns in the input will be equal. Originally, all this question's test cases featured inputs with an equal number of rows and columns. This was a result of poorly chosen test cases and was not intended to indicate that this would be the case for all inputs.
• Your program either needs to output a single consistent value of your choice if filling exactly the squares specified by the input with L-trominoes is possible, and any other value if it is impossible, or vice versa. For example, you may decide to output false if the input shape can be filled, in which case that is the only acceptable output for shapes that can be filled, and any output except false is acceptable for input shapes that can't be filled.
• However, the output of your program must not vary between runs given identical input, if said input is valid. That means if you have output 2 for some particular valid input, any later runs with exactly that input must also output 2.
• This is code-golf - make your code as short as you can.

Examples

The examples use 1 and 0 to represent squares that should and shouldn't be filled respectively, uses true as the only output for fillable shapes, and false as the only output for non-fillable shapes.

1  -> false

0 1
1 1 -> true

1 1 1
1 1 1
1 1 1 -> false

0 1 0
1 1 1
0 0 1  -> false

1 0 0
1 1 1
0 1 1  -> true

1 1 0
1 0 1
1 1 1
1 0 1  -> false

1 1 1 1
1 0 0 1
1 0 0 1
1 1 1 1  -> true

0 1 1 1
1 1 0 1
1 1 1 1
0 1 1 0  -> true

0 1 1 1
1 1 1 1
1 1 1 0
0 1 1 0  -> true

1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 0  -> true

1 1 1 1 1
1 0 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1  -> false

1 1 1 1 0
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1  -> true

Answer 1

JavaScript (ES6),  196 ... 185  182 bytes

Takes input as a binary matrix. Returns a Boolean value.

f=m=>!/1/.test(m)||m.some((r,y)=>r.some((v,x)=>v&&[0,1,2,3].some(d=>([X,V]=(g=d=>[v=x+--d%2,R=m[y+--d%2]||0,R[v]])(d))[2]&g(d+1&3)[2]&&(r[x]=V[X]=R[r[x]=V[X]=R[v]=0,o=f(m),v]=1)&o)))

Try it online!

This algorithm is too slow for the penultimate test case on TIO, but it does find the answer on my laptop in about 90 seconds.

How?

This is a brute force search that looks for all possible trominos in the input matrix and attempts to remove them (one at a time) until the matrix is cleared or all combinations are proven to fail.

Given a reference cell at \$(x,y)\$ (in blue below) and a direction \$0\le d\le 3\$:

• We invoke the helper function \$g\$ with \$d\$ to get a first neighbor cell (in yellow) whose coordinates are x+(d-2)%2 and y+(d-1)%2.
• We invoke \$g\$ again with \$(d+1)\bmod 4\$ to get a second neighbor cell (in red).

This gives:

Commented

f = m =>                         // f is a recursive function taking the matrix m[]
  !/1/.test(m) ||                // stop if m[] does not contain any 1 anymore (success)
  m.some((r, y) =>               // otherwise, for each row r[] at position y in m[]:
    r.some((v, x) =>             //   for each value v at position x in r[]:
      v &&                       //     abort right away if this cell is already empty
      [0, 1, 2, 3].some(d =>     //     otherwise, for each direction d:
        ( [X, V] = (             //       get the 1st neighbor cell
            g = d => [           //       g is a helper function taking a direction
                                 //       and returning the corresponding neighbor cell:
              v = x + --d % 2,   //         save the x-coordinate in v
              R = m[y + --d % 2] //         extract the row R[]
                  || 0,          //         (0 is used as a default object to prevent
                                 //         an access to an undefined row)
              R[v]               //         get the value of the cell
            ]                    //         return the tuple [v, R, value]
          )(d)                   //
        )[2] &                   //       get the value of the 1st neighbor cell
        g(d + 1 & 3)[2]          //       get the value of the 2nd neighbor cell
        && (                     //       if both neighbor cells are set, this is a
          r[x] = V[X] = R[       //       valid L-tromino:
            r[x] =               //         remove it by clearing the current cell
            V[X] = R[v] = 0,     //         and its 2 neighbors
            o = f(m),            //         save the result of a recursive call in o
            v                    //         and restore the tromino
          ] = 1                  //
        ) & o                    //         yield the result of the recursive call
      )                          //     end of loop over the directions
    )                            //   end of loop over the columns
  )                              // end of loop over the rows

Answer 2

APL (Dyalog Unicode), 81 bytes^SBCS

L←⊂⍤2⊢4 2 2⍴∘.≠⍨⍳4
{∧/~,⍵:1⋄∨/∇¨⍵∘{r c l←-⍵⋄⍺>c⌽r⊖(⍴⍺)↑L⊃⍨-l}¨⍸{∧/∘,¨L≤⊂⍵}⌺2 2⊢⍵}

Try it online!

Monadic dfn that takes a binary matrix and gives 1 if it can be tiled with L-triominoes, 0 otherwise.

A brute-force recursive search by removing one triomino at a time. Uses the fact that every orientation of an L-triomino fits within a 2x2 box, so the code tests all 2x2 submatrices of the input array to search for possible L-triomino placements. The Stencil operator ⌺ fits perfectly for this purpose.

The algorithm becomes much faster if we limit the branches to the first 5 placements (which is guaranteed to include all possible placements that includes the top-left cell) at the cost of 8 bytes (⊢↑⍨5⌊≢):

L←⊂⍤2⊢4 2 2⍴∘.≠⍨⍳4
{∧/~,⍵:1⋄∨/∇¨⍵∘{r c l←-⍵⋄⍺>c⌽r⊖(⍴⍺)↑L⊃⍨-l}¨(⊢↑⍨5⌊≢)⍸{∧/∘,¨L≤⊂⍵}⌺2 2⊢⍵}

Try it online!

Ungolfed with comments

⍝ 4 rotations of L-triomino; looks like
⍝ ┌───┬───┬───┬───┐
⍝ │0 1│1 0│1 1│1 1│
⍝ │1 1│1 1│0 1│1 0│
⍝ └───┴───┴───┴───┘
L←,{0@(⊂⍵)⊢2 2⍴1}¨⍳2 2
                  ⍳2 2  ⍝ Indexes of 2-by-2 matrix
   {      ⊢2 2⍴1}¨      ⍝ For each, modify [1 1][1 1] so that
    0@(⊂⍵)              ⍝   that position becomes 0
  ,                     ⍝ Flatten top level

⍝ Main function; 1 if L-triomino tiling is possible, 0 otherwise
f←{
  ⍝ If no cells left, return True
  ∧/~,⍵: 1
    ~,⍵     ⍝ Boolean negation of flattened input matrix
  ∧/        ⍝ All; reduce by And
       : 1  ⍝ If true, return 1

  ⍝ Get possible placements as (row_idx, col_idx, L_idx) triples
  places←⍸{∧/∘,¨L≤⊂⍵}⌺2 2⊢⍵
          {         }⌺2 2⊢⍵  ⍝ Map over 2x2 submatrices...
           ∧/∘,¨L≤⊂⍵  ⍝ Can each of L be placed on a submatrix?
                L≤⊂⍵  ⍝   Compare each cell of each of L with each cell of the submatrix
                      ⍝   so that L(1) vs. ⍵(0) gives False and anything else gives True
           ∧/∘,¨      ⍝   Reduce by And on all cells of each comparison matrix
         ⍸            ⍝ Indexes of ones
  places←             ⍝ Assign to places

  ⍝ For each possible placement, remove the cells and
  ⍝ recursively try L-triomino placements
  ⍝ If no possible placement, ∨/ automatically gives False
  ∨/∇¨⍵∘{r c l←-⍵⋄⍺>c⌽r⊖(⍴⍺)↑L⊃⍨-l}¨places
      ⍵∘{                         }¨places  ⍝ Map each on the places...
         r c l←-⍵⋄                  ⍝ Dissect the placement; negate due to built-in rotation direction
                             L⊃⍨-l  ⍝ Fetch the target L-triomino
                        (⍴⍺)↑       ⍝ Overtake to fit the size of input matrix
                    c⌽r⊖            ⍝ Rotate to move the L-triomino to correct position
                  ⍺>                ⍝ Remove L-triomino cells from input matrix
    ∇¨  ⍝ Recursively test for L-triomino placements
  ∨/    ⍝ True if at least one is successful
}

Answer 3

Python 3, 136 bytes

lambda S:g(int("".join(s.rjust(6,"0")for s in S),2))<1
g=lambda b:b*all(b>>i&t^t or g(t<<i^b)for i in range(25)for t in(67,131,193,194))

Try it online!

Input: A list of strings, each string must be a binary string of the same length.
Output: True if the shape can be tiled, False otherwise.

Explanation:

Approach this problem using bitboard.

Constructing the bitboard:

int("".join(s.rjust(6,"0")for s in S),2)

Recursive function that returns 0 if the shape can be tiled, or a positive integer if the shape cannot be tiled.

g=lambda b:b*all(b>>i&t^t or g(t<<i^b)for i in range(25)for t in(67,131,193,194))