Another Solution
This is, in my opinion, one of the most interesting problems on the site. I need to thank deadcode for bumping it back up to the top.
^((^|xx)(^|\3\4\4)(^|\4x{12})(^x|\1))*$
39 bytes, without any conditionals or assertions... sort of. The alternations, as they're being used (^|), are a type of conditional in a way, to select between "first iteration," and "not first iteration."
This regex can be seen to work here: http://regex101.com/r/qA5pK3/1
Both PCRE and Python interpret the regex correctly, and it has also been tested in Perl up to n = 128, including n4-1, and n4+1.
Definitions
The general technique is the same as in the other solutions already posted: define a self-referencing expression which on each subsequent iteration matches a length equal to the next term of the forward difference function, Df, with an unlimited quantifier (*). A formal definition of the forward difference function:
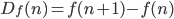
Additionally, higher order difference functions may also be defined:
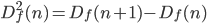
Or, more generally:
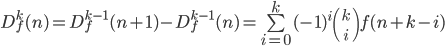
The forward difference function has a lot of interesting properties; it is to sequences what the derivative is to continuous functions. For example, Df of an nth order polynomial will always be an n-1th order polynomial, and for any i, if Dfi = Dfi+1, then the function f is exponential, in much the same way that the derivative of ex is equal to itself. The simplest discrete function for which f = Df is 2n.
f(n) = n2
Before we examine the above solution, let's start with something a bit easier: a regex which matches strings whose lengths are a perfect square. Examining the forward difference function:
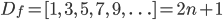
Meaning, the first iteration should match a string of length 1, the second a string of length 3, the third a string of length 5, etc., and in general, each iteration should match a string two longer than the previous. The corresponding regex follows almost directly from this statement:
^(^x|\1xx)*$
It can be seen that the first iteration will match only one x, and each subsequent iteration will match a string two longer than the previous, exactly as specified. This also implies an amazingly short perfect square test in perl:
(1x$_)=~/^(^1|11\1)*$/
This regex can be further generalized to match any n-gonal length:
Triangular numbers:
^(^x|\1x{1})*$
Square numbers:
^(^x|\1x{2})*$
Pentagonal numbers:
^(^x|\1x{3})*$
Hexagonal numbers:
^(^x|\1x{4})*$
etc.
f(n) = n3
Moving on to n3, once again examining the forward difference function:
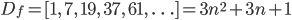
It might not be immediately apparent how to implement this, so we examine the second difference function as well:
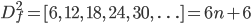
So, the forwards difference function does not increase by a constant, but rather a linear value. It's nice that the initial ('-1th') value of Df2 is zero, which saves an initialization on the second iteration. The resulting regex is the following:
^((^|\2x{6})(^x|\1))*$
The first iteration will match 1, as before, the second will match a string 6 longer (7), the third will match a string 12 longer (19), etc.
f(n) = n4
The forward difference function for n4:

The second forward difference function:
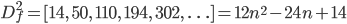
The third forward difference function:
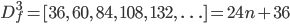
Now that's ugly. The initial values for Df2 and Df3 are both non-zero, 2 and 12 respectively, which will need to be accounted for. You've probably figured out by now that the regex will follow this pattern:
^((^|\2\3{b})(^|\3x{a})(^x|\1))*$
Because the Df3 must match a length of 12 on the second iteration, a is necessarily 12. But because it increases by 24 each term, the next deeper nesting must use its previous value twice, implying b = 2. The final thing to do is initialize the Df2. Because Df2 influences Df directly, which is ultimately what we want to match, its value can be initialized by inserting the appropriate atom directly into the regex, in this case (^|xx). The final regex then becomes:
^((^|xx)(^|\3\4{2})(^|\4x{12})(^x|\1))*$
Higher Orders
A fifth order polynomial can be matched in with the following regex:
^((^|\2\3{c})(^|\3\4{b})(^|\4x{a})(^x|\1))*$
f(n) = n5 is a fairly easy excercise, as the initial values for both the second and fourth forward difference functions are zero:
^((^|\2\3)(^|\3\4{4})(^|\4x{30})(^x|\1))*$
For six order polynomials:
^((^|\2\3{d})(^|\3\4{c})(^|\4\5{b})(^|\5x{a})(^x|\1))*$
For seventh order polynomials:
^((^|\2\3{e})(^|\3\4{d})(^|\4\5{c})(^|\5\6{b})(^|\6x{a})(^x|\1))*$
etc.
Note that not all polynomials can be matched in exactly this way, if any of the necessary coefficients are non-integer. For example, n6 requires that a = 60, b = 8, and c = 3/2. This can be worked around, in this instance:
^((^|xx)(^|\3\6\7{2})(^|\4\5)(^|\5\6{2})(^|\6\7{6})(^|\7x{60})(^x|\1))*$
Here I've changed b to 6, and c to 2, which have the same product as the above stated values. It's important that the product doesn't change, as a·b·c·… controls the constant difference function, which for a sixth order polynomial is Df6. There are two initialization atoms present: one to initialize Df to 2, as with n4, and the other to initialize the fifth difference function to 360, while at the same time adding in the missing two from b.
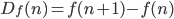
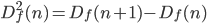
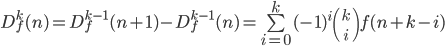
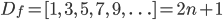
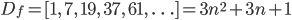
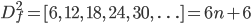

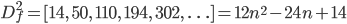
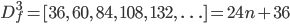
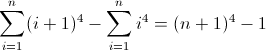
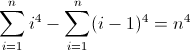
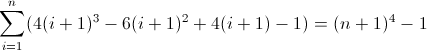
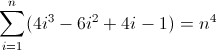
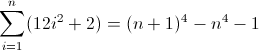
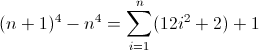
"xx" isn't valid, is it? – Kendall Frey – 2014-01-23T20:32:43.957
@KendallFrey: Nope. It is not valid. – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-01-23T20:34:23.680
@nhahtdh do you think there is a possible answer to that? – xem – 2014-01-23T20:49:28.677
@xem: I have found and verify the answer up to 2^16. – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-01-23T20:51:03.523
you mean lengths up to 2^16 power 4? – xem – 2014-01-23T20:56:59.650
@xem: I mean I tested against string length 0 to 2^16. Which means n was from 0 to 16. – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-01-23T21:00:11.353
I'm pretty sure this is impossible using "true" regular expressions; it's easy to prove (e.g. by the Myhill-Nerode theorem) that the language of strings whose length is a fourth power is not regular. You're going to need some kind of "extended" regexps to solve this.
– Ilmari Karonen – 2014-01-23T21:29:37.007@IlmariKaronen: This question does not limit the syntax to theoretical regular expression. Just that it doesn't allow arbitrary code execution as allowed in Perl. Other stuffs such as backref, etc. are allowed – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-01-23T21:32:34.860
Am I right in assuming that you know a solution to this in at least one regex flavour? – Timwi – 2014-01-23T23:17:07.850
@Timwi Yup, he knows. I've found the solution for
n^2, now I need to work it out forn^4:) – HamZa – 2014-01-23T23:28:15.6731@Timwi: Yes. Java, PCRE (probably Perl also, but can't test), .NET. Mine doesn't work in Ruby/JS, though. – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-01-23T23:42:55.137
In your post you say that "strings of length 0, 1, 16, 81, etc. are valid". Even if I assume you meant
64=4^3instead of81-3^4I still have to ask, why is the empty string allowed? – Kaya – 2014-02-24T16:53:10.633@Kaya: I think you misunderstood my question. I am asking for length n to the 4th power (n^4). I even wrote that in the question. Empty string is allowed, since 0^4 = 0. – n̴̖̋h̷͉̃a̷̭̿h̸̡̅ẗ̵̨́d̷̰̀ĥ̷̳ – 2014-02-24T17:44:27.107
For sure--thanks for the clarification. This is indeed what occurred. – Kaya – 2014-02-24T19:09:41.717
1
This question has been added to the Stack Overflow Regular Expression FAQ, under "Advanced Regex-Fu".
– aliteralmind – 2014-04-10T01:33:37.327