Billiard balls collision

Question

Given the 2-dimensional positions and velocities of a pair of billiard balls right before impact, calculate their velocities after a perfectly elastic collision. The balls are assumed to be ideal spheres (or equivalently: circles) with the same radius, same mass, uniform density, and no friction.

Input consists of 8 numbers: p0x,p0y,v0x,v0y,p1x,p1y,v1x,v1y where p0x,p0y is the centre of the first ball, v0x,v0y its velocity, and similarly p1x,p1y,v1x,v1y for the second ball. You can accept input in any order and structured in any convenient way, e.g. as a 2x2x2 array, or maybe a 2x2 array for p and two length-2 arrays for v0 and v1. It's also fine to take complex numbers (if your language supports them) instead of xy pairs. However, you should not take input in a coordinate system other than Cartesian, i.e. polar is not allowed.

Note that the radius of a billiard ball is half the distance between p0x,p0y and p1x,p1y, so it's not given as an explicit part of the input.

Write a program or function that outputs or returns 4 numbers in any convenient Cartesian representation: the post-collision values of v0x,v0y,v1x,v1y.

A possible algorithm is:

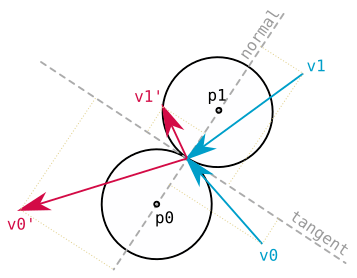
• find the normal line that passes through both centres

• find the tangent line that passes through the midpoint between the two centres and is perpendicular to the normal line

• change coordinate system and break down v0x,v0y and v1x,v1y into their tangential and normal components v0t,v0n and v1t,v1n

• swap the normal components of v0 and v1, preserving their tangential components

• change back to the original coordinate system

Tests (results rounded to 5 decimal places):

   p0x   p0y   v0x   v0y   p1x   p1y   v1x   v1y ->      v0x'       v0y'       v1x'       v1y'
[-34.5,-81.8, 34.7,-76.1, 96.2,-25.2, 59.2,-93.3] [  49.05873, -69.88191,  44.84127, -99.51809]
[ 36.9, 77.7,-13.6,-80.8, -7.4, 34.4, 15.1,-71.8] [   5.57641, -62.05647,  -4.07641, -90.54353]
[-51.0, 17.6, 46.1,-80.1, 68.6, 54.0,-35.1,-73.9] [ -26.48927,-102.19239,  37.48927, -51.80761]
[-21.1,-52.6,-77.7, 91.5, 46.0, 94.1, 83.8, 93.7] [ -48.92598, 154.40834,  55.02598,  30.79166]
[ 91.3, -5.3, 72.6, 89.0, 97.8, 50.5, 36.2, 85.7] [  71.73343,  81.56080,  37.06657,  93.13920]
[-79.9, 54.9, 92.5,-40.7,-20.8,-46.9,-16.4, -0.9] [  47.76727,  36.35232,  28.33273, -77.95232]
[ 29.1, 80.7, 76.9,-85.1,-29.3,-49.5,-29.0,-13.0] [  86.08581, -64.62067, -38.18581, -33.47933]
[ 97.7,-89.0, 72.5, 12.4, 77.8,-88.2, 31.5,-34.0] [  33.42847,  13.97071,  70.57153, -35.57071]
[-22.2, 22.6,-61.3, 87.1, 67.0, 57.6,-15.3,-23.1] [ -58.90816,  88.03850, -17.69184, -24.03850]
[-95.4, 15.0,  5.3, 39.5,-54.7,-28.5, -0.7,  0.8] [  21.80656,  21.85786, -17.20656,  18.44214]
[ 84.0,-26.8,-98.6,-85.6,-90.1, 30.9,-48.1, 37.2] [ -89.76828, -88.52700, -56.93172,  40.12700]
[ 57.8, 90.4, 53.2,-74.1, 76.4,-94.4,-68.1,-69.3] [  51.50525, -57.26181, -66.40525, -86.13819]
[ 92.9, 69.8,-31.3, 72.6,-49.1,-78.8,-62.3,-81.6] [-123.11680, -23.48435,  29.51680,  14.48435]
[-10.3,-84.5,-93.5,-95.6, 35.0, 22.6, 44.8, 75.5] [ -11.12485,  99.15449, -37.57515,-119.25449]
[ -3.9, 55.8,-83.3,  9.1, -2.7,-95.6, 37.7,-47.8] [ -82.84144, -48.75541,  37.24144,  10.05541]
[-76.5,-88.4,-76.7,-49.9, 84.5, 38.0,  4.2, 18.4] [   6.52461,  15.43907, -79.02461, -46.93907]
[ 64.2,-19.3, 67.2, 45.4,-27.1,-28.7, 64.7, -4.3] [  59.66292,  44.62400,  72.23708,  -3.52400]
[  9.8, 70.7,-66.2, 63.0,-58.7, 59.5, 83.7,-10.6] [  68.07646,  84.95469, -50.57646, -32.55469]
[ 62.9, 46.4, 85.0, 87.4, 36.3,-29.0,-63.0,-56.3] [  23.53487, -86.82822,  -1.53487, 117.92822]
[ -5.5, 35.6, 17.6,-54.3, -2.2, 66.8,-15.2, 11.8] [  24.15112,   7.63786, -21.75112, -50.13786]

Shortest wins. No loopholes.

---

thanks @Anush for helping fix the diagram's background colour

Answer 1

Python 3, 67 66 bytes, 53 bytes

def f(p,v,q,w):p-=q;d=((v-w)/p).real*p;return v-d,w+d

Try it online!

-1 byte thanks to @ngn

-13 bytes thanks to @Neil

This function f takes four complex numbers as input and returns two complex numbers. The ungolfed version is shown in the following.

Ungolfed

def elastic_collision_complex(p1, v1, p2, v2):
    p12 = p1 - p2
    d = ((v1 - v2) / p12).real * p12
    return v1 - d, v2 + d

Try it online!

The computation formula is derived based on the 2D-vector formula on wiki. Since \$m_1=m_2\$, the formula can be simplified to $$\left\{\begin{array}{l} v_1'=v_1-dv \\ v_2'=v_2+dv\end{array}\right.$$

Let \$x_{12}=x_1-x_2\$ and \$v_{12}=v_1-v_2\$, we have

$$dv=\frac{\langle v_{12}, x_{12}\rangle}{\|x_{12}\|^2}x_{12} = \frac{Re(v_{12}\cdot\overline{x_{12}})}{x_{12}\cdot \overline{x_{12}}}x_{12}=Re\left(\frac{v_{12}\cdot\overline{x_{12}}}{x_{12}\cdot \overline{x_{12}}}\right)x_{12}=Re\left(\frac{v_{12}}{x_{12}}\right)x_{12}$$

In the ungolfed program, p12, v1 - v2, d correspond to \$x_{12}\$, \$y_{12}\$, and \$dv\$, respectively.

Answer 2

JavaScript (Node.js), 90 88 bytes

(m,n,o,p,q,r,s,t,u=(q-=m)*q+(r-=n)*r,v=o*q+p*r-s*q-t*r)=>[o-(q*=v/u),p-(v*=r/u),s+q,t+v]

Try it online! Link includes test suite. Explanation: q,r are repurposed as the difference vector between the centres, and u is the square of its length. v is the difference in the dot products of o,p and s,t with q,r, so v/u is the scaling factor for q,r that gives the amount of velocity transferred from o,p to s,t. Edit: Saved 2 bytes thanks to @Arnauld.

Answer 3

Perl 6, 75 64 63 61 bytes

11 bytes saved by switching from map to for, dispensing with the need to put things into intermediate variables for the map to see.

1 byte saved by changing ($^a-$^c)².&{$_/abs} to ($^a-$^c).&{$_/.conj}.

2 bytes saved thanks to @nwellnhof.

{(.($^b+$^d,{$_/.conj}($^a-$^c)*($b-$d).conj)/2 for *-*,*+*)}

Try it online!

---

Explanation

When the original post said that the input could be complex numbers, it was too hard to resist... So this takes 4 complex numbers (position 1, velocity 1, position 2, velocity 2) and returns the velocities as complex numbers.

The program uses just the same algorithm as described in the OP. However, with complex numbers, that is quite simple. First, let's notice that the complex number \$d = p_1 - p_0\$ points from the first ball to the second. So if we divide all the velocities by it, the normal direction suddenly coincides with the real axis and the tangent direction with the imaginary axis. (This messes up the magnitudes but we don't care.)

Now, we need to switch the normal (i. e. real) parts of the velocities \$v_0/d\$ and \$v_1/d\$, and after that, multiply it by \$d\$ again to make the normal (and the velocities) point in the correct direction (and to unmess the magnitudes). So we need to calculate $$ \begin{align*} v_0' &= d \left( \Re \frac{v_1}{d} + \mathrm{i} \Im \frac{v_0}{d} \right), \\ v_1' &= d \left( \Re \frac{v_0}{d} + \mathrm{i} \Im \frac{v_1}{d} \right) \end{align*} $$ (where \$\Re\$ = real part, \$\Im\$ = imaginary part). Let's shuffle the first one a bit (using \$\star\$ for complex conjugation): $$ v_0' = d \left( \Re \frac{v_1}{d} + \mathrm{i} \Im \frac{v_0}{d} \right) = d \left[ \frac 1 2 \left( \frac{v_1}{d} + \frac{v_1^\star}{d^\star} \right) + \frac 1 2 \left( \frac{v_0}{d} - \frac{v_0^\star}{d^\star} \right) \right] =\ = \frac d 2 \left( \frac{v_0 + v_1}{d} - \frac{v_0^\star - v_1^\star}{d^\star} \right) = \frac 1 2 \left( v_0 + v_1 - \frac{d}{d^\star} (v_0^\star - v_1^\star) \right).$$ The result for \$v_1'\$ can be obtained just by switching \$v_0 \leftrightarrow v_1\$. All that does is changing a sign: $$ v_1' = \frac 1 2 \left[ v_0 + v_1 + \frac{d}{d^\star} \left(v_0^\star - v_1^\star\right) \right]. $$

And that's it. All the program does is just this calculation, golfed a bit.

Answer 4

C (gcc), 140 132 bytes

f(m,n,o,p,q,r,s,t,a)float*a,m,n,o,p,q,r,s,t;{q-=m;r-=n;m=q*q+r*r,n=o*q+p*r-s*q-t*r;q*=n/m;*a++=o-q;n*=r/m;*a++=p-n;*a++=s+q;*a=t+n;}

Try it online!

Basically a port of @Neil's JavaScript answer, but then @ceilingcat shaved off 8 bytes by cleverly reusing m and n to store temporaries.

Answer 5

Jelly, 16 bytes

_/×ḋ÷²S¥_/ʋ¥N,$+

Try it online!

A dyadic link taking as its left argument a list of the initial positions [[p0x, p0y], [p1x, p1y]] and its right argument the initial velocities [[v0x, v0y], [v1x, v2y]]. Returns a list of the final velocities [[v0x', v0y'], [v1x', v2y']]

Based on the algorithm used by @Neil’s JavaScript answer so be sure to upvote that one too!

Answer 6

Python 2, 97 92 bytes

m,n,o,p,q,r,s,t=input()
q-=m
r-=n
a=o*q+p*r-s*q-t*r
a/=q*q+r*r
print o-a*q,p-a*r,s+a*q,t+a*r

Try it online!

Modified version of Neil's approach.

Answer 7

C (gcc), 77 72 bytes

f(p,v,q,w,a)_Complex*a,p,v,q,w;{p-=q;p*=creal((v-w)/p);*a=v-p;a[1]=w+p;}

Try it online!

Based on the python implementation of @Joel

Answer 8

APL (Dyalog Classic), 21 bytes

⊢/-{,∘-⍨×/(9○÷⍨)\-⌿⍵}

Try it online!

based on @Joel's answer

in: 2x2 complex matrix, out: complex pair