12
A simple Manufactoria challenge. Compute the input modulo 7. The input will be in big-endian binary (blue=1, red=0). The output should be in the same format.
Test cases provided. The smallest part count wins.
(if the input mod 7 is 0, output nothing.)
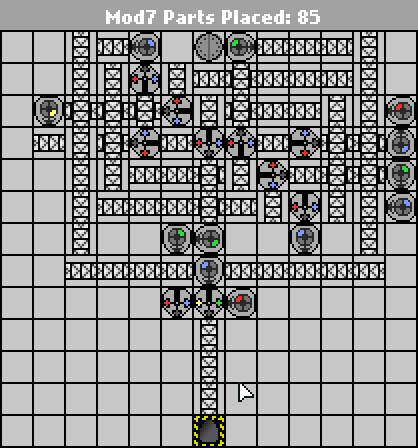
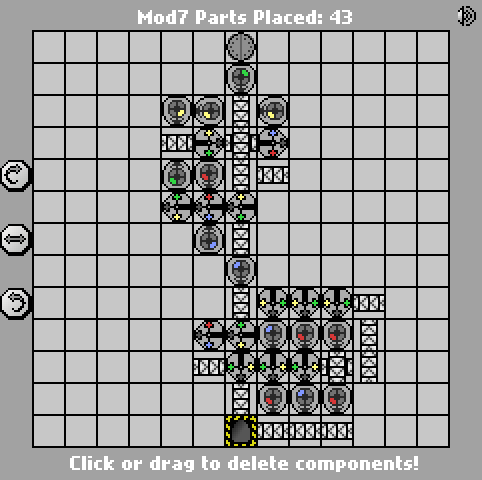


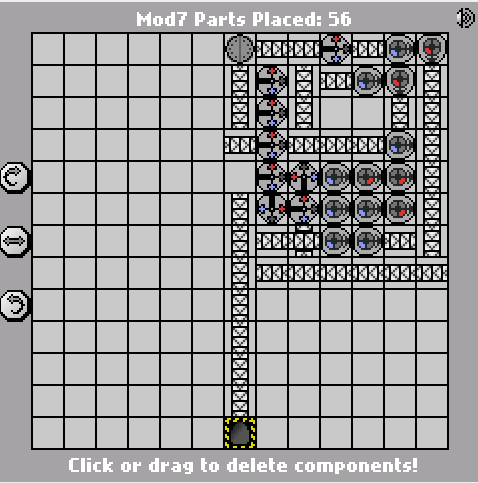
"code-golf" in this case means "fewest parts"? – John Dvorak – 2014-01-21T06:02:52.747
Since I haven't even solved the incrementation problem, I have no idea how to solve this. Manufactoria is fun. – Justin – 2014-01-21T06:15:42.823
@JanDvorak: yes. – Keith Randall – 2014-01-21T07:02:12.400
@KeithRandall We never tagged [tag:code-golf] with manufactoria. We should either remove the tag here or add it to the other questions. – Howard – 2014-01-21T08:26:19.460
@Howard: I'd say add it (or [tag:fastest-code] or [tag:busy-beaver] or [tag:code-challenge] or whatever best describes the scoring), and let [tag:manufactoria] be a simple language tag.
– Ilmari Karonen – 2014-01-28T14:15:22.520