Write The Shortest Program To Check If A Binary Tree Is Balanced

Question

For each node in a balanced binary tree, the maximum difference in the heights of the left child subtree and the right child subtree are at most 1.

The height of a binary tree is the distance from the root node to the node child that is farthest from the root.

Below is an example:

           2 <-- root: Height 1
          / \
         7   5 <-- Height 2
        / \   \
       2   6   9 <-- Height 3
          / \  /
         5  11 4 <-- Height 4 

Height of binary tree: 4

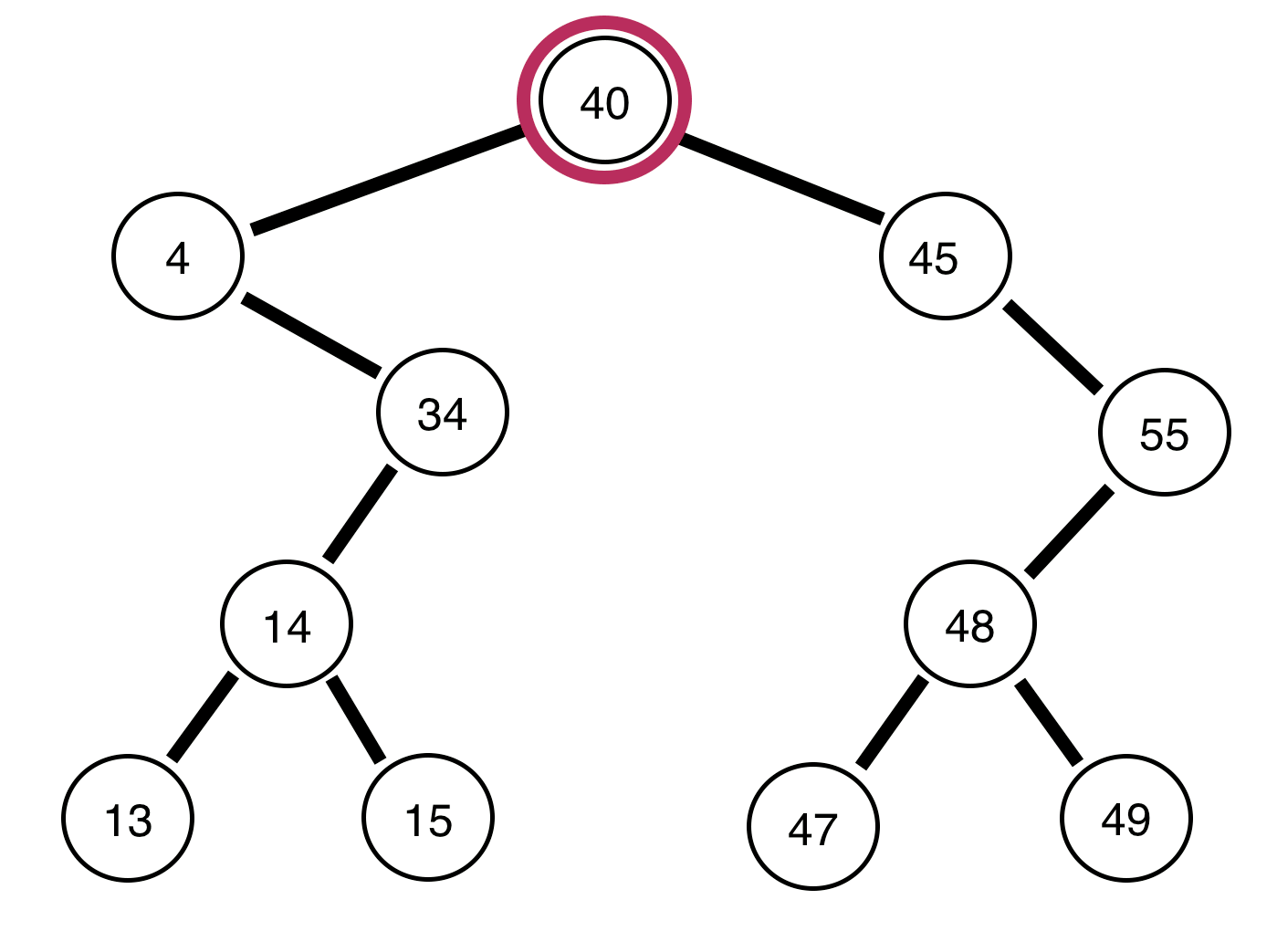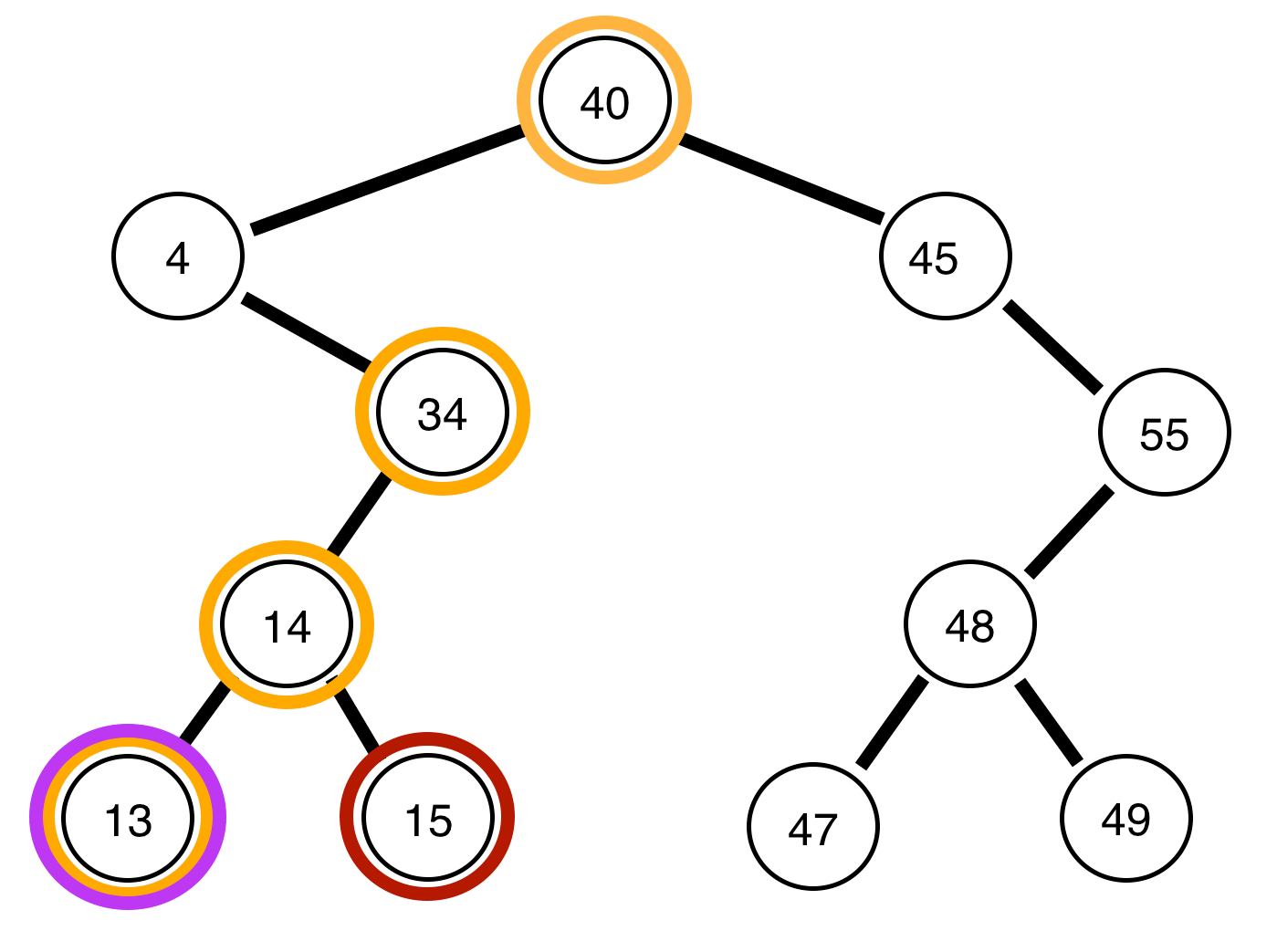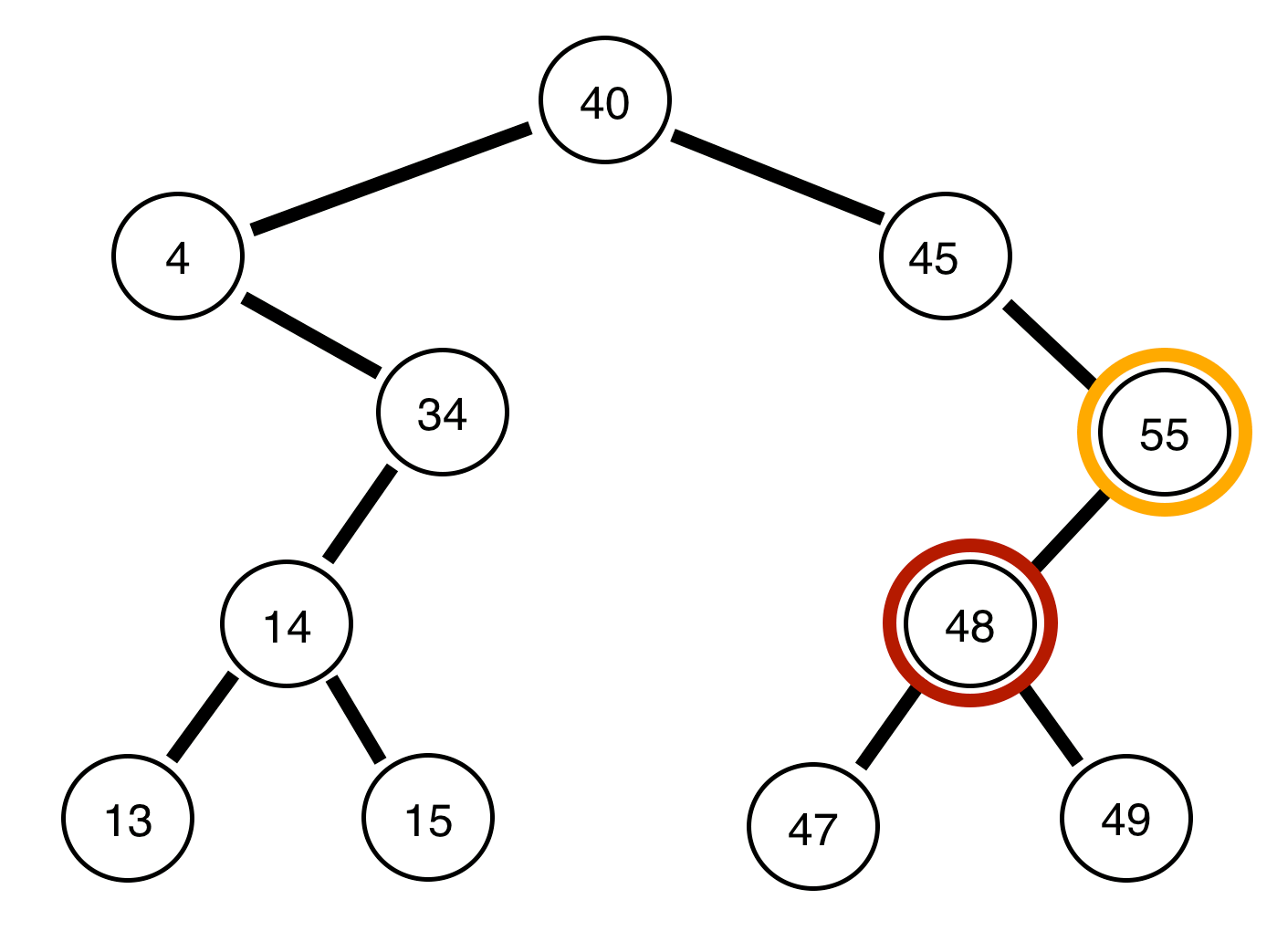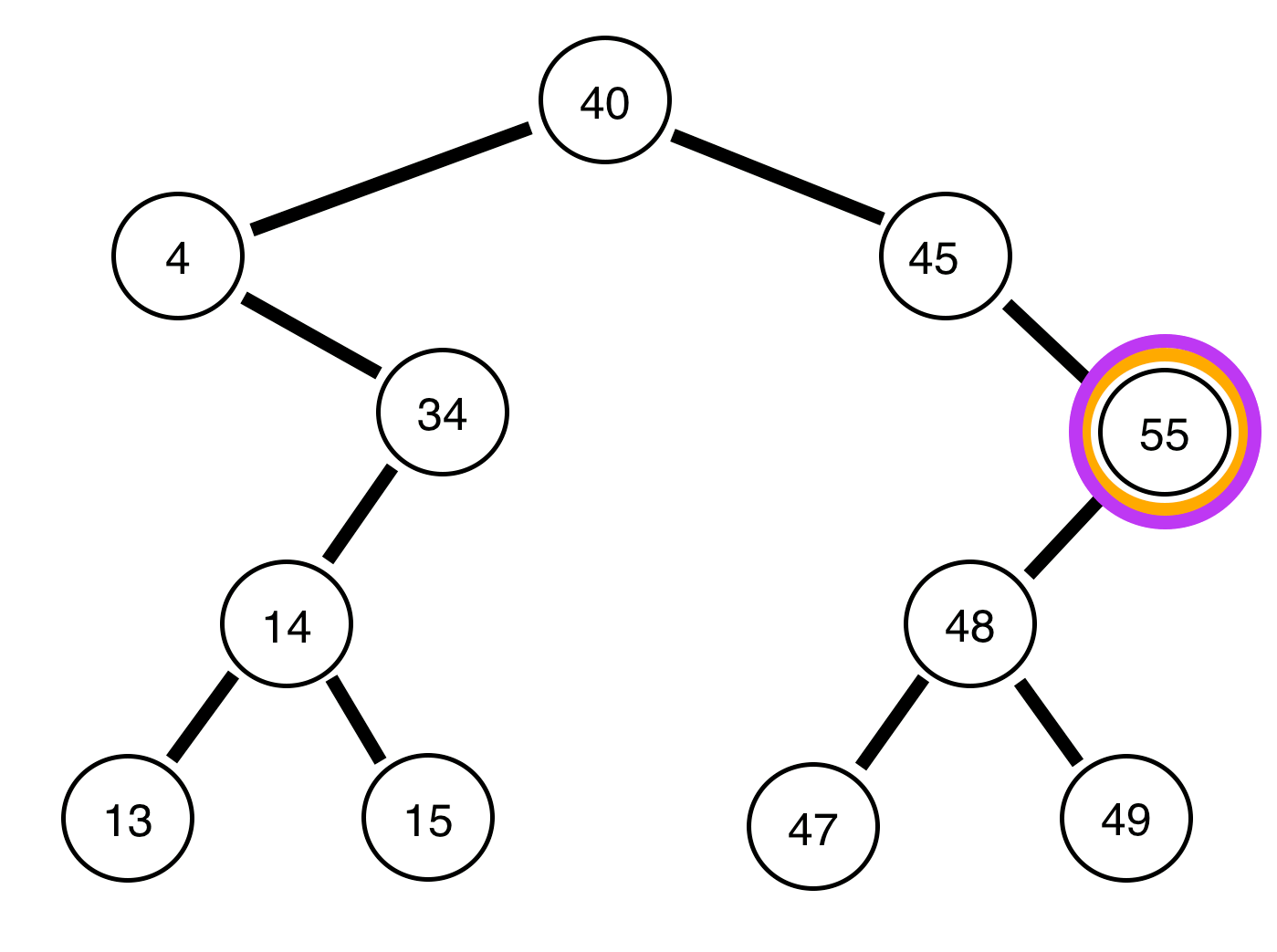
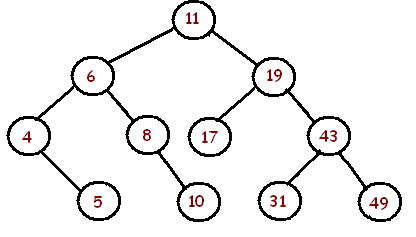
The following are binary trees and a report on whether or not they are balanced:

The tree above is unbalanced.

The above tree is balanced.

Write the shortest program possible that accepts as input the root of a binary tree and returns a falsey value if the tree is unbalanced and a truthy value if the tree is balanced.

Input

The root of a binary tree. This may be in the form of a reference to the root object or even a list that is a valid representation of a binary tree.

Output

Returns truthy value: If the tree is balanced

Returns falsey value: If the tree is unbalanced.

Definition of a Binary Tree

A tree is an object that contains a value and either two other trees or pointers to them.

The structure of the binary tree looks something like the following:

typedef struct T
{
   struct T *l;
   struct T *r;
   int v;
}T;

If using a list representation for a binary tree, it may look something like the following:

[root_value, left_node, right_node]

Answer 1

Jelly, 11 bytes

ḊµŒḊ€IỊ;߀Ạ

Try it online!

The empty tree is represented by [].

Answer 2

Prolog (SWI), 49 bytes

N+_/B/C:-X+B,Y+C,abs(X-Y)<2,N is max(X,Y)+1.
0+e.

Try it online!

Represents trees as Value/Left_Child/Right_Child, with the empty tree being the atom e. Defines +/2, which outputs through success or failure, with an unbound variable (or one already equal to the tree's height) on the left and the tree on the right--if the height argument is unacceptable, add 9 bytes to define -T:-_+T..

N + _/B/C :-            % If the second argument is a tree of the form _Value/B/C,
    X+B,                % X is the height of its left child which is balanced,
    Y+C,                % Y is the height of its right child which is balanced,
    abs(X-Y) < 2,       % the absolute difference between X and Y is strictly less than 2,
    N is max(X,Y)+1.    % and N is the height of the full tree.
0 + e.                  % If, on the other hand, the second argument is e, the first is 0.

Answer 3

JavaScript (Node.js), 49 bytes

h=([l,r])=>l?(d=h(l)-h(r))*d<2?1+h(d>0?l:r):NaN:1

Try it online!

-9 bytes by Arnauld.

---

JavaScript, 58 bytes

h=([l,r])=>l?(l=h(l),r=h(r),m=l>r?l:r,m+m-l-r<2?m+1:NaN):1

Try it online!

Use [] for null, and [left, right, value] for nodes.

Answer 4

Wolfram Language (Mathematica), 50 bytes

f@_[x_,y_]:=f@x&&f@y&&-2<Depth@x-Depth@y<2;f@_=1>0

Use Null for null, value[left, right] for nodes. For example, the following tree is written as 2[7[2[Null, Null], 6[5[Null, Null], 11[Null, Null]]], 5[Null, 9[4[Null, Null], Null]]].

    2
   / \
  7   5
 / \   \
2   6   9
   / \  /
  5  11 4

Try it online!

Answer 5

Python 3.8 (pre-release), 133 125 bytes

b=lambda t:((max(l[0],r[0])+1,abs(l[0]-r[0])<2)if(l:=b(t[1]))[1]and(r:=b(t[2]))[1]else(0,0))if t else(0,1)
h=lambda t:b(t)[1]

Try it online!

Takes a tree in the "list" format: A node is [value, left, right] with left and right being nodes.

Invoke the function h.

Returns 0 or False for an unbalanced tree. Returns 1 or True for a balanced tree.

Ungolfed:

# Returns tuple (current height, subtrees are balanced (or not))
def balanced(tree):
  if tree: # [] evaluates to False
    left = balanced(tree[1])
    right = balanced(tree[2])
    # If  the subtrees are not both balanced, nothing to do, just pass it up
    if left[1] and right[1]:
      height = max(left[0], right[0]) + 1
      subtrees_balanced = abs(left[0] - right[0]) < 2
    else:
      height = 0 # Value doesn't matter, will be ignored
      subtrees_balanced = False
  else:
    height = 0
    subtrees_balanced = True
  return (height, subtrees_balanced)

def h(tree):
  return balanced(tree)[1]

-10: Reversed logic to get rid of nots

If taking arguments in the middle of a call is allowed, this could be shortened to (115 bytes)

(b:=lambda t:((max(l[0],r[0])+1,abs(l[0]-r[0])<2)if(l:=b(t[1]))[1]and(r:=b(t[2]))[1]else(0,0))if t else(0,1))(_)[1]

with _ being the tree to check.

Answer 6

JavaScript, 162 bytes

f=x=>{for(f=0,s=[[x,1]];s[0];){if(!((d=(t=s.pop())[0]).a&&d.b||f))f=t[1];if(f&&t[1]-f>1)return 0;if(d.a)s.push([d.a,t[1]+1]);if(d.b)s.push([d.b,t[1]+1])}return 1}

Try it online!

The format of the input is an object

root={a:{node},b:{node},c:value}

Explanation

for(f=0,s=[[x,1]];s[0];){if(!((d=(t=s.pop())[0]).a&&d.b||f))f=t[1]

Performing breadth first search find the depth of the first node which is missing one or more branches.

if(f&&t[1]-f>1)return 0;if(d.a)s.push([d.a,t[1]+1]);if(d.b)s.push([d.b,t[1]+1])}

Continuing the breadth first search, return zero if any element is two deeper than the depth of the first node missing branches.

return 1}

If no such node is found, return 1

Answer 7

Julia, 56 bytes

f(t)=t!=()&&(-(f.(t.c)...)^2<2 ? maximum(f,t.c)+1 : NaN)

With the following struct representing the binary tree:

struct Tree
    c::NTuple{2,Union{Tree,Tuple{}}}
    v::Int
end

c is a tuple representing the left and right nodes and the empty tuple () is used to signal the absence of a node.

Falsey value is NaN, any integer is truthy.

Answer 8

Kotlin, 67 bytes

fun N.c():Int=maxOf(l?.c()?:0,r?.c()?:0)+1
fun N.b()=l?.c()==r?.c()

Where

data class N(val l: N? = null, val r: N? = null, val v: Int = 0)

Try it online!

Answer 9

Python 2, 99 96 94 bytes

lambda A:A==[]or(abs(D(A[1])-D(A[2]))<2)*f(A[1])*f(A[2])
D=lambda A:A>[]and-~max(map(D,A[1:]))

Try it online!

3 bytes from Jo King.

Takes input as: empty node is [], and other nodes are [<value>, <leftNode>, <rightNode>]. Outputs 0/1 for False/True.

Answer 10

C, 117 bytes

h(T*r){r=r?1+h(h(r->l)>h(r->r)?r->l:r->r):0;}b(T*r){return r->l&&!b(r->l)||r->r&&!b(r->r)?0:abs(h(r->l)-h(r->r))<=1;}

Struct implementation is the following:

 typedef struct T
    {
        struct T * l;

        struct T * r;

        int v;

    } T;

Try This on JDoodle