39
6
Rules
You will start with only two elements: Points \$A\$ and \$B\$ such that \$A \neq B\$. These points occupy a plane that is infinite in all directions.
At any step in the process you may do any of the three following actions:
Draw a line that passes through two points.
Draw a circle centered at one point such that another point lies on the circle.
Add a new point where two objects (lines and circles) intersect.
Your goal is to create 5 points such that they form the vertices of a regular pentagon (a convex polygon with 5 sides equal in length) using as few circles as possible. You may of course have other points but 5 of them must for a regular pentagon. You do not have to draw the edges of the pentagon for your scoring.
Scoring
When comparing two answers the one that draws fewer circles is better. In the case of a tie in circles the answer that draws the fewest lines is better. In the case of a tie in both circles and lines the answer that adds the fewest points is better.
Anti-Rules
While the rules list is exhaustive and details everything you can do this list is not, just because I don't say you can't do something does not mean you can.
You cannot create "arbitrary" objects. Some constructions you will find will do thinks like add a point at an "arbitrary" location and work from there. You cannot add new points at locations other than intersections.
You cannot copy a radius. Some constructions will involve taking a compass setting it to a radius between two points and then picking it up and drawing a circle elsewhere. You cannot do this.
You cannot perform limiting processes. All constructions must take a finite number of steps. It is not good enough to approach the answer asymptotically.
You cannot draw an arc or part of a circle in order to avoid counting it as a circle in your scoring. If you want to visually use arcs when showing or explaining your answer because they take up less space go ahead but they count as a circle for scoring.
Tools
You can think through the problem on GeoGebra. Just go over to the shapes tab. The three rules are equivalent to the point, line and circle with center tools.
Burden of Proof
This is standard but I would like to reiterate. If there is a question as to whether a particular answer is valid the burden of proof is on the answerer to show that their answer is valid rather than the public to show that the answer is not.
What is this doing on my Code-Golf site?!
This is a form of atomic-code-golf similar to proof-golf albeit in a bit of a weird programming language. There is currently a +22/-0 consensus on the meta that this sort of thing is allowed.
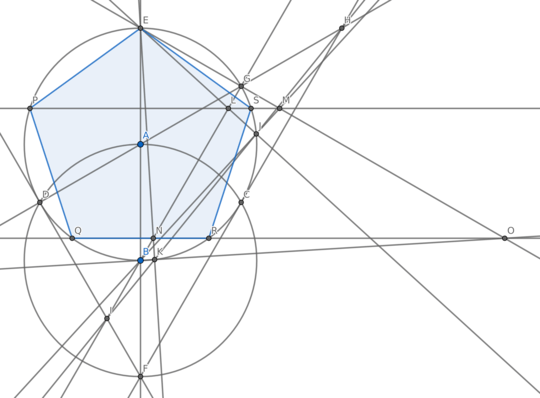
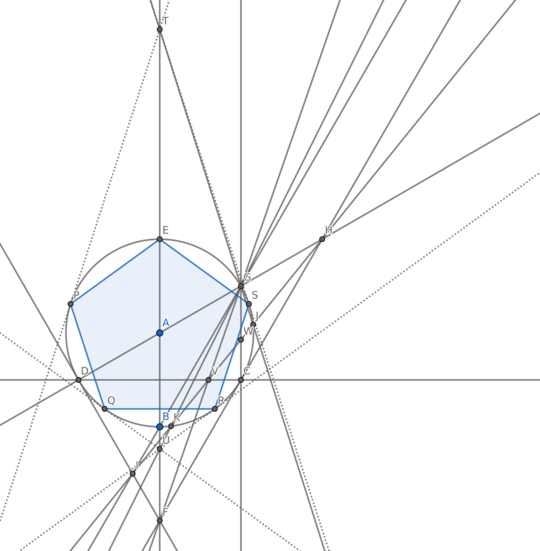

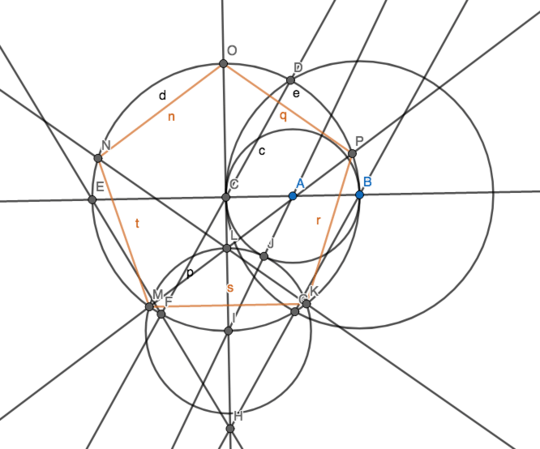
12This is like the game I have on my phone called Euclidea. – mbomb007 – 2019-07-13T16:40:40.463
closely related: https://codegolf.stackexchange.com/q/38653/15599
– Level River St – 2019-07-13T17:03:20.373"setting it two a radius" a likely typo – Grzegorz Oledzki – 2019-07-13T17:34:24.793
6Next time you should ask people to draw a heptagon, which would be slightly more challenging:) – flawr – 2019-07-13T18:09:55.167
@flawr "Slightly", hmm? – aschepler – 2019-07-14T03:33:47.200
If I remember correctly, a 13-gon is possible, so that would be quite challenging. – mbomb007 – 2019-07-14T18:20:54.187
3It's the regular 17-gon which is constructible using ruler and compasses. I can give you a heptagon but it won't necessarily be regular! – Rosie F – 2019-07-14T18:25:23.073
1
Heptagon (7 sides) is not possible with only ruler and compass. Mathologer covered it.
– Draco18s no longer trusts SE – 2019-07-14T19:00:25.310If the 17-gon is too easy, there's always the regular 65537-gon... – Neil – 2019-07-14T21:06:51.517
Are answers supposed to actually prove/explain why the resulting pentagon is regular? It's not obvious to me just by following the construction. – Minethlos – 2019-07-15T14:49:21.447
@Minethlos Answers don't have to prove there correctness by default but the burden of proof is on the answerer. If don't follow why an answer should be regular just leave a comment asking for clarification. – Post Rock Garf Hunter – 2019-07-15T14:53:46.097