44
8
The purpose of this challenge is to graphically depict a walk on the plane, where the direction of each step \$k\$ is determined by the primality of \$k\$ and the parity of its binary expansion. Specifically,
- Initial direction is fixed, say North.
- All steps have the same length.
- The direction of step \$k\$ can be North, West, South or East, and is determined as follows:
- If \$k\$ is not prime, the direction does not change.
- If \$k\$ is prime and the binary expansion of \$k\$ has an even number of ones, turn right.
- If \$k\$ is prime and the binary expansion of \$k\$ has an odd number of ones, turn left.
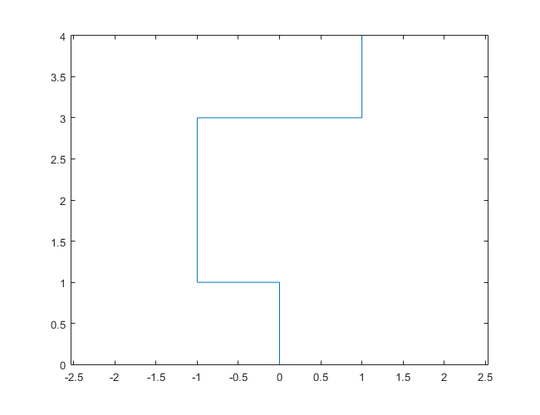
As a worked example, assume that the initial direction is North. The first steps are:
- \$k=1\$ is not prime. So we move one step in the current direction, which is North.
- \$k=2\$ is prime, and its binary expansion,
10, has and odd number of ones. So we turn left, and are now facing West. We move one step in that direction. - \$k=3\$ is prime, and its binary expansion,
11, has and even number of ones. So we turn right, and are now facing North. We move one step in that direction. - \$k=4\$ is not prime. So we move one step in the current direction, which is North.
The challenge
Input: positive integer \$N\$.
Output: plot of the \$N\$-step walk as defined above.
Additional rules
- The initial direction can be freely chosen (not necessarily North), but should be the same for all \$N\$.
- The turning rule can be the opposite to that described above, that is, turn right for odd parity and left for even; but it has to be the same for all \$N\$.
- The output has to be a graphical depiction of the walk. For instance:
- The walk can be drawn with line segments.
- The visited points can be shown with a marker, such as a dot; with or without connecting line segments.
- A two-colour raster image can be provided, with one colour corresponding to visited points and another for non-visited.
- The scales of the horizontal and vertical axes need not be the same. Also axis labels and similar elements are optional. As long as the walk can be clearly seen, the plot is valid.
- Note that some points are visited more than once. The plot is not sensitive to this. For instance, if line segments are shown in the plot, each unit segment is displayed the same no matter how many times it has been traversed.
- The code should work for any
Ngiven unlimited resources. It is acceptable if in practice it fails for largeNdue to time, memory or data-type limitations. - Input and output are flexible as usual. In particular, any of the standard means for outputting images can be used.
- The shortest code in bytes wins.
Test cases
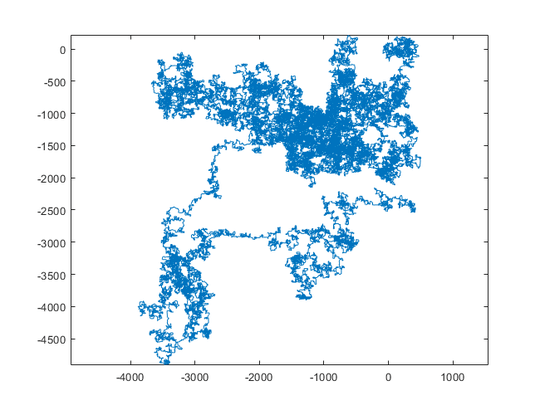
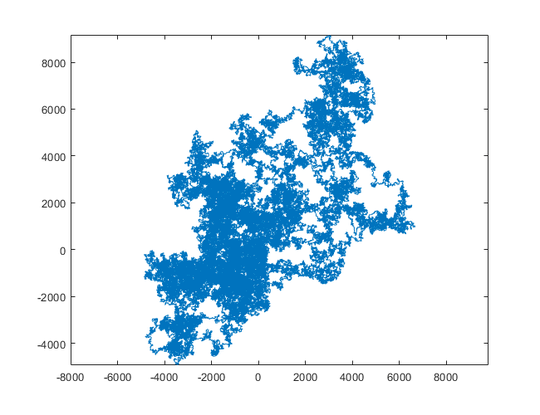
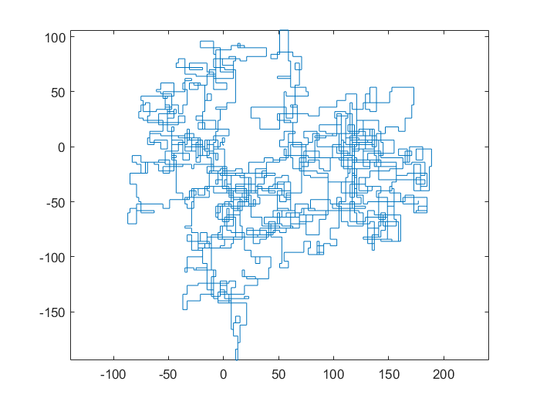
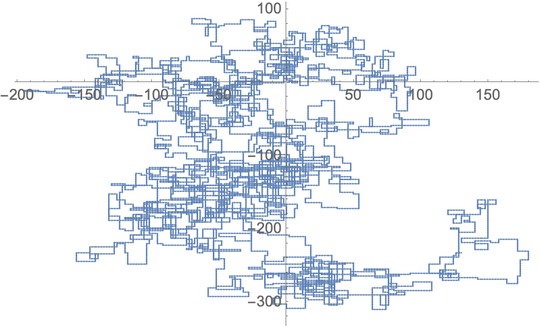
The following plots use North as initial direction; even parity turns right; and the walk is depicted with line segments.
N = 7:
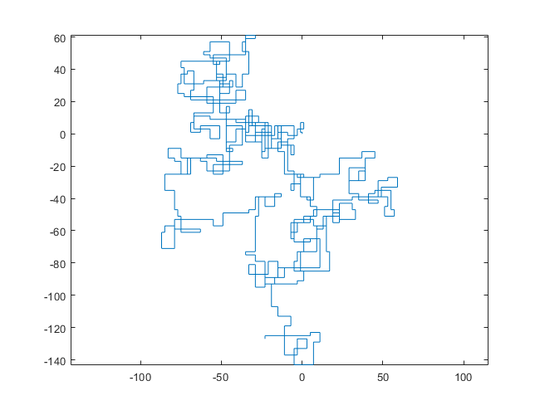
N = 3000:
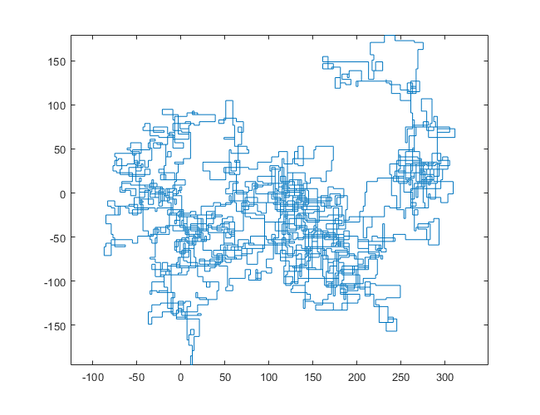
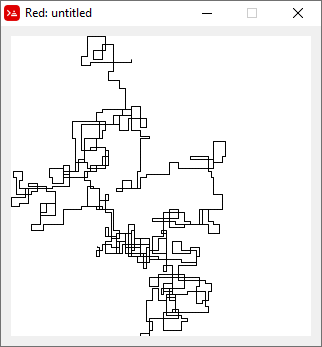
N = 20000:
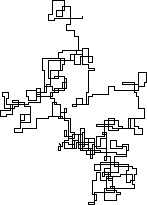
N = 159000:
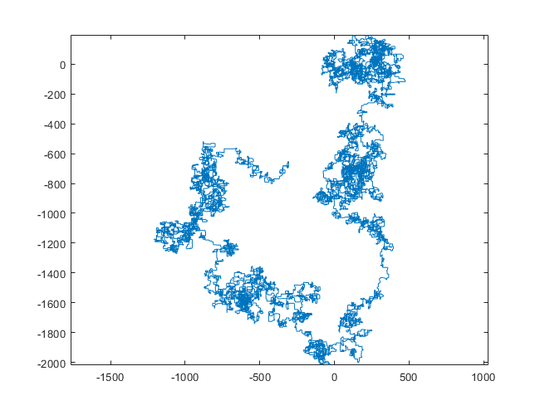
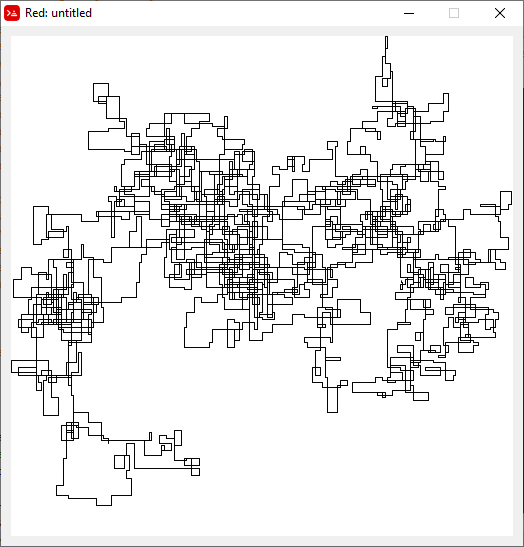
N = 1200000:
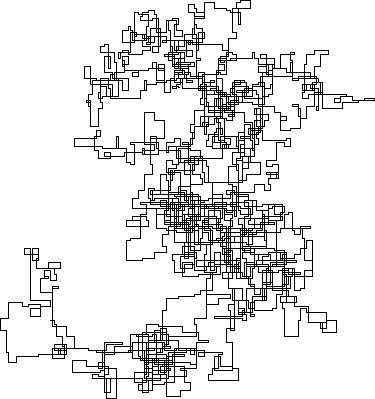
N = 11000000:



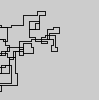
1Is there a reason only
[graphical-output]is allowed? Any reason in particular to disallowed ASCII output, like my now deleted Charcoal answer? – Kevin Cruijssen – 2019-06-24T12:11:20.6602@Kevin I was advised once not to mix both in the same challenge... What do others think? – Luis Mendo – 2019-06-24T12:34:53.693
1Well, I can understand the reasoning behind that advice, since output as image/graph vs ASCII art is completely different in some languages. Then again, I have seen graph outputs getting loads of upvotes in ASCII-art challenges and vice-versa, so I guess not everyone agrees. Personally I think it really depends on the challenge. In this case I personally don't see any harm in allowing both in the same challenge, but maybe I'm biased due to my now deleted answer. So I'll ask the same question as you: "What do others think?" @Arnauld Maybe you should post your ASCII Taxi Driver after all ;) – Kevin Cruijssen – 2019-06-24T12:42:41.720
@KevinCruijssen Yes, perhaps a good compromise is to post another similar challenge for ASCII art. – Luis Mendo – 2019-06-24T13:43:21.923
1Would be interesting to see this run on various OEIS sequences (true, some would just walk in a straight line or run in circles, but some could be quite something). – Draco18s no longer trusts SE – 2019-06-24T14:31:20.020
1@Draco18s Yup. I tried a few things and many give nice looking paths – Luis Mendo – 2019-06-24T14:33:15.597
@LuisMendo out of curiosity, is this your invention, or is this a studied sequence? – Jonah – 2019-06-24T16:29:57.527
1
@Jonah I came up with it (but there are similar walks that are probably well known; see for example here). I wanted a random-looking but reproducible walk. And I wanted it change direction not too often. So primes came to mind (random-looking, not too abundant). Also I wanted for it to change direction left or right with the same probability. The parity of a prime number is obviously not useful for this. So parity of the sum of binary digits was a natural choice
– Luis Mendo – 2019-06-24T16:36:35.78016At N=11000000, it appears to be approximating the map of Europe. – Digital Trauma – 2019-06-24T18:07:02.563
1
@DigitalTrauma Also, https://chat.stackoverflow.com/transcript/message/46585109#46585109
– Luis Mendo – 2019-06-24T18:32:19.350@DigitalTrauma This phenomenon is known as pareidolia. That said, I do agree that it looks like a map of Europe. ;)
– Arnauld – 2019-06-25T13:29:36.237