Mathematica
Nepal's Interim Constitution - Schedule 1 (rel. to Article 6), pp. 260 and 262, provides 25 detailed instructions about how to construct the flag. (see http://www.ccd.org.np/resources/interim.pdf). The numbers in the comments refer to the corresponding instructions in the constitution.
We will need functions to draw equilateral triangles and determine the distance from a point to a line:
ClearAll[triangle]
triangle[a_?NumericQ,b_?NumericQ,c_?NumericQ,labeled_:True]:=
Block[{x,y,pt,sqr},sqr=#.#&;
pt[a1_,b1_,c1_]:=Reduce[sqr[{x,y}]==b1^2&&sqr[{x,y}-{a1,0}]==c1^2&&y>0,{x,y}];
{(
(*Polygon[{{0,0},{a,0},{x,y}}]*)
Polygon[{{-a/2(*0*),0},{a/2,0},{x-a/2,y}}]),
If[labeled,
{Text[Style[Framed[a,Background->LightYellow],11],{a/2,0}],
Text[Style[Framed[b,Background->LightYellow],11],{x/2,y/2}],
Text[Style[Framed[c,Background->LightYellow],11],{(a+x)/2,y/2}]},{}]}/.ToRules[pt[a,b,c]]]
(*distance from point to a line *)
dist[line_,{x0_,y0_}]:=(Abs[a x0+b y0+c]/.{x0-> m[[1]],y0-> m[[2]]})/Sqrt[a^2+b^2]; (* used below *)
The remaining code, with numbers referring to the instructions. By far, the most challenging part is to make the rays for the moon and the sun. GeometricalTransformation comes in handy for doing translations and rotations.
(*shape inside flag*)
(*1*)
w=100;a={0,0};b={w,0};
lAB=Line[{a,b}];
tA=Text["A",Offset[{-10,-20},a]];
tB=Text["B",Offset[{20,-20},b]];
(*2*)
c={0,w 4/3};d={0,w};
lAC=Line[{a,c}];
tC=Text["C",Offset[{-10,20},c]];
lAD=Line[{a,d}];
tD=Text["D",Offset[{-10,0},d]];
lBD=Line[{b,d}];
(*3*)
e=Solve[(x-w)^2+y^2==(w)^2&&y==w-x,{x,y}][[1,All,2]];
tE=Text["E",Offset[{15,0},e]];
(*4*)
f={0,e[[2]]};tF=Text["F",Offset[{-10,0},f]];
g={w,e[[2]]};tG=Text["G",Offset[{15,0},g]];
lFG=Line[{f,g}];
poly={a,b,e,g,c};
(*5*)lCG= Line[{c,g}];
(*moon*)
(*6*)
lineCG=N[((f[[2]]-c[[2]])/w)x+c[[2]](*100*)];
h={w/4,0};tH=Text["H",Offset[{0,-20},h]];
i={h[[1]],lineCG/.x->h[[1]]};tI=Text["I",Offset[{10,0},i]];
lHI={Dashed, LightGray,Line[{h,i}]};
(*7*)
j={0,f[[2]]+(c[[2]]-f[[2]])/2};tJ=Text["J",Offset[{-10,10},j]];
lineJG=N[((f[[2]]-j[[2]])/g[[1]])x+j[[2]]];
k={Solve[lineCG==j[[2]],x][[1,1,2]],j[[2]]};tK=Text["K",Offset[{10,10},k]];
(*k={Solve[lineCG\[Equal]c[[2]],x][[1,1,2]],j[[2]]};tK=Text["K",Offset[{10,10},k]];*)
lJK={Dashed, LightGray,Line[{j,k}]};
(*8*)l={i[[1]],j[[2]]};tL=Text["L",Offset[{0,10},l]];
(*9*)lJG={LightGray,Dashed,Line[{j,g}]};
(*10*)m={h[[1]],(lineJG/.x-> h[[1]])};tM=Text["M",Offset[{0,10},m]];
(*11*)distMfromBD=dist[{1,1,-w(*100*)},m];
n={i[[1]],m[[2]]-distMfromBD};tN=Text["N",Offset[{0,0},n]];
(*ln=Abs[l[[2]]-n[[2]]];*)
(*12*)o={0,m[[2]]};tO=Text["O",Offset[{-10,0},o]];
lM={Dashed,LightGray,Line[{o,{g[[1]],o[[2]]}}]};
(*13*)
radiusLN=l[[2]]-n[[2]];
p={m[[1]]-radiusLN,m[[2]]};tP=Text["P",Offset[{0,10},p]];
q={m[[1]]+radiusLN,m[[2]]};tQ=Text["Q",Offset[{0,10},q]];
moonUpperEdge={White,Circle[l,radiusLN,{Pi,2 Pi}]};
moonLowerEdge={White,Circle[m,radiusMQ,{Pi,2 Pi}]};
(*14*)radiusMQ=q[[1]]-m[[1]];
(*15*)radiusNM=m[[2]]-n[[2]];
arc={Yellow,Circle[n,radiusNM,{Pi/7,6 Pi/7}]};
{r,s}=Solve[(x-l[[1]])^2+(y-l[[2]])^2==(radiusLN)^2 &&(x-n[[1]])^2+(y-n[[2]])^2==(radiusNM)^2,{x,y}][[All,All,2]];
tR=Text["R",Offset[{0,0},r]];
tS=Text["S",Offset[{0,0},s]];
t={h[[1]],r[[2]]};
tT={Black,Text["T",Offset[{0,0},t]]};
(*16*)radiusTS=Abs[t[[1]]-s[[1]]];
(*17*)radiusTM=Abs[t[[2]]-m[[2]]];
(*18 triangles*)
t2=Table[GeometricTransformation[GeometricTransformation[triangle[4,4,4,False][[1]],RotationTransform[k Pi/8]],{TranslationTransform[t]}],{k,-4,3}];
midRadius=(Abs[radiusTM+radiusTS]/2-2);
pos=1;table2=GeometricTransformation[t2[[pos++]],{TranslationTransform[#]}]&/@Table[midRadius {Cos@t,Sin[t]},{t,Pi/16,15 Pi/16,\[Pi]/8}];
(*19 sun*)u={0,f[[2]]/2};tU=Text["U",Offset[{-10,0},u]];
lineBD=N[(d[[2]]/w)x+d[[2]]];
v={-Solve[lineBD==u[[2]],x][[1,1,2]],u[[2]]};tV=Text["V",Offset[{10,0},v]];
lUV={LightGray,Dashed,Line[{u,v}]};
(*20*)w={h[[1]],u[[2]]};tW={Black,Text["W",Offset[{0,0},w]]};
(*21*)
(*22*)
t3=Table[GeometricTransformation[GeometricTransformation[triangle[9,9,9,False][[1]],RotationTransform[k Pi/6]],{TranslationTransform[w]}],{k,-3,9}];
midRadius3=(Abs[radiusTM+radiusTS]/2+2.5);
pos=1;
table3=GeometricTransformation[t3[[pos++]],{TranslationTransform[#]}]&/@Table[midRadius3 {Cos@t,Sin[t]},{t,0,2 Pi,2\[Pi]/12}];
Show[
Graphics[{Gray,
(*1*)lAB,tA,tB,
(*2*)lAC,tC,lAD,tD,lBD,
(*3*)tE,
(*4*)tF,lFG,tG,{Red,Opacity[.4],Polygon[poly]},
(*5*)lCG,
(*6*)tH,lCG,tI,lHI,
(*7*)tJ,lJK,tK,
(*8*)tL,
(*9*)lJG,
(*10*)tM,
(*11*)tN,
(*12*)lM,tO,
(*13*)moonUpperEdge,tP,tQ,
(*14*)moonLowerEdge,
(*15*)arc,tR,tS,tT,
(*16*){White,Dashed,Circle[t,radiusTS(*,{0, Pi}*)]},
(*17*){White,Opacity[.5],Disk[t,radiusTM,{0, 2 Pi}]},
(*18 triangles*){White,(*EdgeForm[Black],*)table2},
(*19 sun*)tU,tV,lUV,
(*20*)tW,{Opacity[.5],White,Disk[w,Abs[m[[2]]-n[[2]]]]},
(*21*)Circle[w,Abs[l[[2]]-n[[2]]]],
(*22*){Black(*White*),EdgeForm[Black],triangle[4,4,4,False](*table3*)},
{White,(*EdgeForm[Black],*)table3},
(*23*)
{Darker@Blue,Thickness[.03],Line[{a,b,e,g,c,a}]}
},
Ticks-> None(*{{0,100},{0,80,120,130}}*), BaseStyle-> 16,AspectRatio-> 1.3,Axes-> True],
(*cresent moon*)
RegionPlot[{(x-25)^2+(y-94.19)^2<21.4^2&&(x-25)^2+(y-102.02)^2>21.4^2},{x,0,100},{y,30,130},PlotStyle->{Red,White}]]
The following flag, from the above code, is made according to the instructions in the constitution.
Colors are modified to enable easier viewing of the construction lines.
The letters refer to points and lines in the instructions.
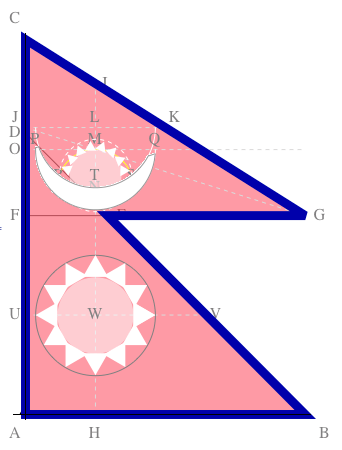
By the way, flags of the world can be called up directly within Mathematica. For example:
Graphics[CountryData["Nepal", "Flag"][[1]], ImageSize->{Automatic,200}]








1Deja vu! Also, how many rows of ASCII text are in 100px? – Kendall Frey – 2014-01-16T22:06:28.973
@KendallFrey Well, ASCII art is one of the ways, to solve this, however there is no answer into your question. as it depends on font size and spacing between lines, answer provider should count it himself. – ST3 – 2014-01-16T22:08:03.357
1In that case, surely
print("|\\\n|\\")is a valid solution. I think you need to be more specific about the rules for non-bitmap entries. – Kendall Frey – 2014-01-16T22:09:55.630User inputs height of flag that means that generated output if input is 100 and output of 101 should differ, so answer should contain something like
GetTextExtentPoint32to measure output – ST3 – 2014-01-16T22:17:17.4975Please do not delete and repost your question. There's editing for a reason... also, there's no link in your new question. – Doorknob – 2014-01-16T22:17:56.257
@ST3 For ascii output, I recommend saying that each character is a pixel. It makes a lot of sense. – Justin – 2014-01-16T22:59:56.777
1Also, rather than disallowing internet resources, why not require that the flag actually be drawn (ie created by code)? – Justin – 2014-01-16T23:01:05.063
I got a filling there is language that makes it pretty straightforward to code those drawing instructions. ContextFree first comes to mind. Looking forward to it.
– swish – 2014-01-17T00:27:20.807what about a
data:url? =p – Brian Glaz – 2014-01-17T20:41:58.503