Surface of the 3x3x3 cube as a graph

Question

Your task is to generate a graph with 54 vertices, each corresponds to a facet on a Rubik's cube. There is an edge between two vertices iff the corresponding facets share a side.

Rules

• You may choose to output an adjacency list, adjacency matrix, edge list, or any reasonable format to represent a graph in an algorithm. (A visual graph readable by a human is generally not a reasonable format in an algorithm in most cases.)
• You may make either every vertex adjacent to itself, or none adjacent to itself.
• You may either include both directions for each edge (count one or two times for self-loops), or output exactly one time for each edge, but not mix the ways.
• You may renumber the vertices, skip some numbers, or even use non-number labels for the vertices in any way you want. You should also post the numbering if it isn't obvious, so others could check your answer in easier ways.
• This is code-golf. Shortest code in bytes wins.

Example output

This is the numbering of vertices used in the example:

          0  1  2
          3  4  5
          6  7  8
 9 10 11 18 19 20 27 28 29 36 37 38
12 13 14 21 22 23 30 31 32 39 40 41
15 16 17 24 25 26 33 34 35 42 43 44
         45 46 47
         48 49 50
         51 52 53

Output as an adjacency list (vertex number before each list is optional):

0 [1 3 9 38]
1 [2 4 0 37]
2 [29 5 1 36]
3 [4 6 10 0]
4 [5 7 3 1]
5 [28 8 4 2]
6 [7 18 11 3]
7 [8 19 6 4]
8 [27 20 7 5]
9 [10 12 38 0]
10 [11 13 9 3]
11 [18 14 10 6]
12 [13 15 41 9]
13 [14 16 12 10]
14 [21 17 13 11]
15 [16 51 44 12]
16 [17 48 15 13]
17 [24 45 16 14]
18 [19 21 11 6]
19 [20 22 18 7]
20 [27 23 19 8]
21 [22 24 14 18]
22 [23 25 21 19]
23 [30 26 22 20]
24 [25 45 17 21]
25 [26 46 24 22]
26 [33 47 25 23]
27 [28 30 20 8]
28 [29 31 27 5]
29 [36 32 28 2]
30 [31 33 23 27]
31 [32 34 30 28]
32 [39 35 31 29]
33 [34 47 26 30]
34 [35 50 33 31]
35 [42 53 34 32]
36 [37 39 29 2]
37 [38 40 36 1]
38 [9 41 37 0]
39 [40 42 32 36]
40 [41 43 39 37]
41 [12 44 40 38]
42 [43 53 35 39]
43 [44 52 42 40]
44 [15 51 43 41]
45 [46 48 17 24]
46 [47 49 45 25]
47 [33 50 46 26]
48 [49 51 16 45]
49 [50 52 48 46]
50 [34 53 49 47]
51 [52 44 15 48]
52 [53 43 51 49]
53 [35 42 52 50]

Answer 1

APL (Dyalog Classic), 34 30 bytes

-4 thanks to jimmy23013

4≥+/¨|∘.-⍨,(⍳3)∘.⌽7 ¯1∘.,○⍳3 3

Try it online!

outputs an adjacency matrix with each vertex adjacent to itself

⍳3 3 generate an array of (0 0)(0 1)(0 2)(1 0)(1 1)(1 2)(2 0)(2 1)(2 2)

○ multiply all by π

7 ¯1∘., prepend 7 or -1 in all possible ways

(⍳3)∘.⌽ rotate coord triples by 0 1 2 steps in all possible ways

+/¨|∘.-⍨, compute manhattan distance between each pair

4≥ it must be no greater than 4 for neighbouring facets

Answer 2

Ruby, 79 bytes

54.times{|i|p [(i%6<5?i+1:i+18-i/6%3*7)%54,(i+=i%18<12?6:[18-i%6*7,3].max)%54]}

Try it online!

Prints a representation of a unidirectional graph, as a list of the vertices to the right of and below each vertex as shown in the map below.

 0  1  2  3  4  5   
 6  7  8  9 10 11   
12 13 14 15 16 17   
         18 19 20 21 22 23
         24 25 26 27 28 29
         30 31 32 33 34 35
                  36 37 38 39 40 41
                  42 43 44 45 46 47 
                  48 49 50 51 52 53

Answer 3

Python 2.7, 145

def p(n):l=(3-n%2*6,n/6%3*2-2,n/18*2-2);k=n/2%3;return l[k:]+l[:k]
r=range(54)
x=[[sum((x-y)**2for x,y in zip(p(i),p(j)))<5for i in r]for j in r]

Try it online!

Defines an adjacency matrix x as a list of lists of boolean values. Facets count as being adjacent to themselves.

p(n) computes the coordinates of the center of the nth facet of a 3x3x3 cube whose facets are 2 units across. Adjacency is determined by testing if 2 facets have a square distance under 5 (adjacent facets have square distance at most 4, non-adjacent facets have square distance at least 6).

Answer 4

Charcoal, 48 bytes

Ｆ⁷Ｆ⁷Ｆ⁷⊞υ⟦ικλ⟧≔Φυ⁼Φ﹪ι⁶¬﹪λ²⟦⁰⟧υＩＥυΦＬυ⁼²ΣＥ§υλ↔⁻ν§ιξ

Try it online! Link is to verbose version of code. Explanation:

Ｆ⁷Ｆ⁷Ｆ⁷⊞υ⟦ικλ⟧

Generate all sets of 3-dimensional coordinates in the range [0..6] for each dimension.

≔Φυ⁼Φ﹪ι⁶¬﹪λ²⟦⁰⟧υ

Keep only those coordinates that are centres of 2x2 squares on one of the faces x=0, y=0, z=0, x=6, y=6, z=6.

ＩＥυΦＬυ⁼²ΣＥ§υλ↔⁻ν§ιξ

For each coordinate, print the indices of those coordinates whose taxicab distance is 2.

The vertices are numbered as follows:

         33 34 35
         21 22 23
          9 10 11
36 24 12  0  1  2 13 25 37 47 46 45
38 26 14  3  4  5 15 27 39 50 49 48
40 28 16  6  7  8 17 29 41 53 52 51
         18 19 20
         30 31 32
         42 43 44

Answer 5

Wolfram Language 190 bytes

The following returns all of the graph edges in terms of the actual coordinates (assuming each mini-cube is 2 units at the edge and the Rubik's cube has its bottom left vertex at the origin).

t=Table;h[a_,b_,c_]:=t[{x,y,z},{a,1,5,2},{b,1,5,2},{c,0,6,6}];Partition[Sort[a=Cases[DeleteCases[Tuples[Flatten[{h[x,z,y],h[y,z,x],h[x,y,z]},3],{2}],{x_,x_}],x_/;ManhattanDistance@@x==2]],4]

(* output *)
{{{{0,1,1},{0,1,3}},{{0,1,1},{0,3,1}},{{0,1,1},{1,0,1}},{{0,1,1},{1,1,0}}},{{{0,1,3},{0,1,1}},{{0,1,3},{0,1,5}},{{0,1,3},{0,3,3}},{{0,1,3},{1,0,3}}},{{{0,1,5},{0,1,3}},{{0,1,5},{0,3,5}},{{0,1,5},{1,0,5}},{{0,1,5},{1,1,6}}},{{{0,3,1},{0,1,1}},{{0,3,1},{0,3,3}},{{0,3,1},{0,5,1}},{{0,3,1},{1,3,0}}},{{{0,3,3},{0,1,3}},{{0,3,3},{0,3,1}},{{0,3,3},{0,3,5}},{{0,3,3},{0,5,3}}},{{{0,3,5},{0,1,5}},{{0,3,5},{0,3,3}},{{0,3,5},{0,5,5}},{{0,3,5},{1,3,6}}},{{{0,5,1},{0,3,1}},{{0,5,1},{0,5,3}},{{0,5,1},{1,5,0}},{{0,5,1},{1,6,1}}},{{{0,5,3},{0,3,3}},{{0,5,3},{0,5,1}},{{0,5,3},{0,5,5}},{{0,5,3},{1,6,3}}},{{{0,5,5},{0,3,5}},{{0,5,5},{0,5,3}},{{0,5,5},{1,5,6}},{{0,5,5},{1,6,5}}},{{{1,0,1},{0,1,1}},{{1,0,1},{1,0,3}},{{1,0,1},{1,1,0}},{{1,0,1},{3,0,1}}},{{{1,0,3},{0,1,3}},{{1,0,3},{1,0,1}},{{1,0,3},{1,0,5}},{{1,0,3},{3,0,3}}},{{{1,0,5},{0,1,5}},{{1,0,5},{1,0,3}},{{1,0,5},{1,1,6}},{{1,0,5},{3,0,5}}},{{{1,1,0},{0,1,1}},{{1,1,0},{1,0,1}},{{1,1,0},{1,3,0}},{{1,1,0},{3,1,0}}},{{{1,1,6},{0,1,5}},{{1,1,6},{1,0,5}},{{1,1,6},{1,3,6}},{{1,1,6},{3,1,6}}},{{{1,3,0},{0,3,1}},{{1,3,0},{1,1,0}},{{1,3,0},{1,5,0}},{{1,3,0},{3,3,0}}},{{{1,3,6},{0,3,5}},{{1,3,6},{1,1,6}},{{1,3,6},{1,5,6}},{{1,3,6},{3,3,6}}},{{{1,5,0},{0,5,1}},{{1,5,0},{1,3,0}},{{1,5,0},{1,6,1}},{{1,5,0},{3,5,0}}},{{{1,5,6},{0,5,5}},{{1,5,6},{1,3,6}},{{1,5,6},{1,6,5}},{{1,5,6},{3,5,6}}},{{{1,6,1},{0,5,1}},{{1,6,1},{1,5,0}},{{1,6,1},{1,6,3}},{{1,6,1},{3,6,1}}},{{{1,6,3},{0,5,3}},{{1,6,3},{1,6,1}},{{1,6,3},{1,6,5}},{{1,6,3},{3,6,3}}},{{{1,6,5},{0,5,5}},{{1,6,5},{1,5,6}},{{1,6,5},{1,6,3}},{{1,6,5},{3,6,5}}},{{{3,0,1},{1,0,1}},{{3,0,1},{3,0,3}},{{3,0,1},{3,1,0}},{{3,0,1},{5,0,1}}},{{{3,0,3},{1,0,3}},{{3,0,3},{3,0,1}},{{3,0,3},{3,0,5}},{{3,0,3},{5,0,3}}},{{{3,0,5},{1,0,5}},{{3,0,5},{3,0,3}},{{3,0,5},{3,1,6}},{{3,0,5},{5,0,5}}},{{{3,1,0},{1,1,0}},{{3,1,0},{3,0,1}},{{3,1,0},{3,3,0}},{{3,1,0},{5,1,0}}},{{{3,1,6},{1,1,6}},{{3,1,6},{3,0,5}},{{3,1,6},{3,3,6}},{{3,1,6},{5,1,6}}},{{{3,3,0},{1,3,0}},{{3,3,0},{3,1,0}},{{3,3,0},{3,5,0}},{{3,3,0},{5,3,0}}},{{{3,3,6},{1,3,6}},{{3,3,6},{3,1,6}},{{3,3,6},{3,5,6}},{{3,3,6},{5,3,6}}},{{{3,5,0},{1,5,0}},{{3,5,0},{3,3,0}},{{3,5,0},{3,6,1}},{{3,5,0},{5,5,0}}},{{{3,5,6},{1,5,6}},{{3,5,6},{3,3,6}},{{3,5,6},{3,6,5}},{{3,5,6},{5,5,6}}},{{{3,6,1},{1,6,1}},{{3,6,1},{3,5,0}},{{3,6,1},{3,6,3}},{{3,6,1},{5,6,1}}},{{{3,6,3},{1,6,3}},{{3,6,3},{3,6,1}},{{3,6,3},{3,6,5}},{{3,6,3},{5,6,3}}},{{{3,6,5},{1,6,5}},{{3,6,5},{3,5,6}},{{3,6,5},{3,6,3}},{{3,6,5},{5,6,5}}},{{{5,0,1},{3,0,1}},{{5,0,1},{5,0,3}},{{5,0,1},{5,1,0}},{{5,0,1},{6,1,1}}},{{{5,0,3},{3,0,3}},{{5,0,3},{5,0,1}},{{5,0,3},{5,0,5}},{{5,0,3},{6,1,3}}},{{{5,0,5},{3,0,5}},{{5,0,5},{5,0,3}},{{5,0,5},{5,1,6}},{{5,0,5},{6,1,5}}},{{{5,1,0},{3,1,0}},{{5,1,0},{5,0,1}},{{5,1,0},{5,3,0}},{{5,1,0},{6,1,1}}},{{{5,1,6},{3,1,6}},{{5,1,6},{5,0,5}},{{5,1,6},{5,3,6}},{{5,1,6},{6,1,5}}},{{{5,3,0},{3,3,0}},{{5,3,0},{5,1,0}},{{5,3,0},{5,5,0}},{{5,3,0},{6,3,1}}},{{{5,3,6},{3,3,6}},{{5,3,6},{5,1,6}},{{5,3,6},{5,5,6}},{{5,3,6},{6,3,5}}},{{{5,5,0},{3,5,0}},{{5,5,0},{5,3,0}},{{5,5,0},{5,6,1}},{{5,5,0},{6,5,1}}},{{{5,5,6},{3,5,6}},{{5,5,6},{5,3,6}},{{5,5,6},{5,6,5}},{{5,5,6},{6,5,5}}},{{{5,6,1},{3,6,1}},{{5,6,1},{5,5,0}},{{5,6,1},{5,6,3}},{{5,6,1},{6,5,1}}},{{{5,6,3},{3,6,3}},{{5,6,3},{5,6,1}},{{5,6,3},{5,6,5}},{{5,6,3},{6,5,3}}},{{{5,6,5},{3,6,5}},{{5,6,5},{5,5,6}},{{5,6,5},{5,6,3}},{{5,6,5},{6,5,5}}},{{{6,1,1},{5,0,1}},{{6,1,1},{5,1,0}},{{6,1,1},{6,1,3}},{{6,1,1},{6,3,1}}},{{{6,1,3},{5,0,3}},{{6,1,3},{6,1,1}},{{6,1,3},{6,1,5}},{{6,1,3},{6,3,3}}},{{{6,1,5},{5,0,5}},{{6,1,5},{5,1,6}},{{6,1,5},{6,1,3}},{{6,1,5},{6,3,5}}},{{{6,3,1},{5,3,0}},{{6,3,1},{6,1,1}},{{6,3,1},{6,3,3}},{{6,3,1},{6,5,1}}},{{{6,3,3},{6,1,3}},{{6,3,3},{6,3,1}},{{6,3,3},{6,3,5}},{{6,3,3},{6,5,3}}},{{{6,3,5},{5,3,6}},{{6,3,5},{6,1,5}},{{6,3,5},{6,3,3}},{{6,3,5},{6,5,5}}},{{{6,5,1},{5,5,0}},{{6,5,1},{5,6,1}},{{6,5,1},{6,3,1}},{{6,5,1},{6,5,3}}},{{{6,5,3},{5,6,3}},{{6,5,3},{6,3,3}},{{6,5,3},{6,5,1}},{{6,5,3},{6,5,5}}},{{{6,5,5},{5,5,6}},{{6,5,5},{5,6,5}},{{6,5,5},{6,3,5}},{{6,5,5},{6,5,3}}}}

The work of generating the points on each external facet is done by the function, h. It has to be called 3 times to generate the points at x=0, x=6; y=0, y=6; and z=0,z=6.

Each facet point that is a Manhattan distance of 2 units from another will be connected to the respective point.

We can display the graph edges visually by the following; a is the list of graph edges that are represented below as arrows.

Graphics3D[{Arrowheads[.02],Arrow/@a},Boxed->False,Axes-> True]

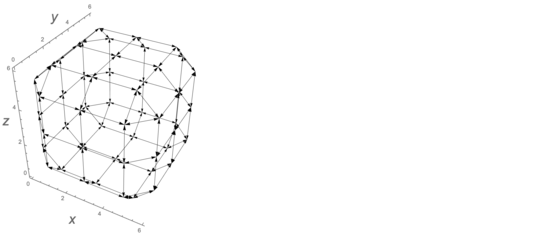
The following shows the Rubik's cube, the points on the external facets, and 8 graph edges.

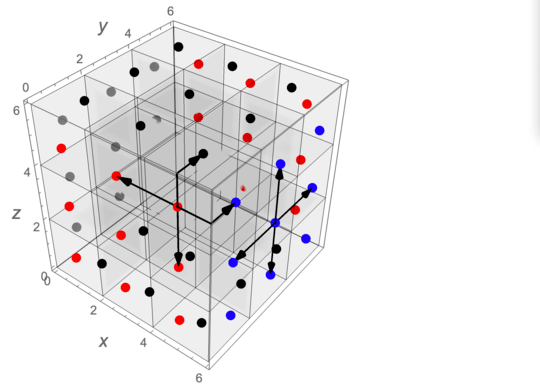
Red dots are located on facets at y = 0 and y = 6; blue and gray dots are on facets at x = 6 and x = 0, respectively; black dots are on facets at z=6 and z=0.

Answer 6

Rust - 278 bytes

fn main(){let mut v=vec![];for x in vec![-2,0,2]{for y in vec![-2,0,2]{for z in vec![-2,2]{v.push([-1,z,x,y]);v.push([0,x,y,z]);v.push([1,x,z,y]);}}}for r in 0..54{print!("\n{} ",r);for s in 0..54{if (0..4).map(|n|v[r][n]-v[s][n]).map(|d|d*d).sum::<i32>()<5{print!("{} ",s)}}}}

Try on play.rust-lang.org

This is big, but the smallest code for a compiled language (so far). It creates an adjacency list. Its very similar to cardboard_box 's python answer but I wanted to see if Quaternions could work.

Step 1: Construct 54 Quaternions, each representing a single facet.

Step 2: for each Quaternion, list all other Quaternions with Quadrance (aka squared distance, aka squared norm of the difference) <= 4.

Quaternions are built like so: The imaginary vectors i j k are points on the shell of a grid, from -2,-2,-2 to 2,2,2, step 2. The real part w is always -1, 0, or 1, so that facets on opposite sides of the cube have the same real part, but adjacent sides have different real parts. The real part allows distinguishing different 'sides' of the cube through calculation.

Quaternion numbering (pseudo isometric 3d view of a cube):

   ->i  ^j  \k

                  -2,+2,+2   +0,+2,+2  +2,+2,+2
                  -2,+0,+2   +0,+0,+2  +2,+0,+2
                  -2,-2,+2   +0,-2,+2  +2,-2,+2
                       w=0

   -2,+2,+2       -2 +2 +2   +0 +2 +2   +2 +2 +2     +2,+2,+2
   -2,+0,+2                                          +2,+0,+2
   -2,-2,+2       -2 -2 +2   +0 -2 +2   +2 -2 +2     +2,-2,+2

     -2,+2,+0       -2 +2 +0   +0 +2 +0   +2 +2 +0     +2,+2,+0
     -2,+0,+0                                          +2,+0,+0
     -2,-2,+0       -2 -2 +0   +0 -2 +0   +2 -2 +0     +2,-2,+0

       -2,+2,-2       -2 +2 -2   +0 +2 -2   +2 +2 -2     +2,+2,-2
       -2,+0,-2             w=1                          +2,+0,-2
       -2,-2,-2       -2 -2 -2   +0 -2 -2   +2 -2 -2     +2,-2,-2
           w=-1             w=1                              w=-1

                       -2,+2,-2   +0,+2,-2  +2,+2,-2
                       -2,+0,-2   +0,+0,-2  +2,+0,-2
                       -2,-2,-2   +0,-2,-2  +2,-2,-2
                            w=0

Indexed numbering (unfolded cube):

                    16 34 52
                    10 28 46
                     4 22 40
         48 30 12   14 32 50  15 33 51
         42 24  6    8 26 44   9 27 45
         36 18  0    2 20 38   3 21 39
                     1 19 37
                     7 25 43
                    13 31 49
                     5 23 41
                    11 29 47
                    17 35 53

Answer 7

JavaScript (ES6, Browser), 153 bytes

for(F=n=>(A=[n%9/3|0,n%3]).splice(n/18,0,(n/9&1)*3-.5)&&A,i=0;i<54;i++)for([a,b,c]=F(i),j=0;j<54;Math.hypot(a-d,b-e,c-f)>1||alert([i,j]),j++)[d,e,f]=F(j)

Try it online!

This is modified to reduce 5 bytes by making same points adjacent, i.e. \$||\mathbf{A-B}||\leq1\$.

JavaScript (ES6, Browser), 158 bytes

for(F=n=>(A=[n%9/3|0,n%3]).splice(n/18,0,(n/9&1)*3-.5)&&A,i=0;i<54;i++)for([a,b,c]=F(i),j=0;j<54;Math.hypot(a-d,b-e,c-f)>1||i-j&&alert([i,j]),j++)[d,e,f]=F(j)

Try it online! (simulates alert with console.log)

Maps the center of all 54 facets to the 3-d space and calculates whether \$0<||\mathbf{A-B}||\leq1\$ for every pair of points. Outputs all directed edges as pairs of numbers [a, b]. The vertex map is

47 50 53
46 49 52
45 48 51
20 23 26 11 14 17 35 32 29  8  5  2 
19 22 25 10 13 16 34 31 28  7  4  1 
18 21 24  9 12 15 33 30 27  6  3  0 
36 39 42
37 40 43
38 41 44