Dyalog APL (75 73 69 68 characters)
Here is another and fifth attempt (most probably my last one); I spent the day trying to write some piece of code shorter than 80 characters and being fully consistent with the rules. This challenge made my day!
I finally got a line of APL made of 75 characters, working with Dyalog APL (but not on the online interpreter page because using the ⍎ execute function), which is the following one:
(N,D)÷D∨N←(⍎'0',1↓I/⍨2=+\P)+(⍎'0',I/⍨2>+\P)×D←D+0=D←⍎'0',⌽2↓⍕¯1+10⊥P←'.'=I← '1.2.3'
Of course I could make it a little shorter, but the special cases where one, two or three fields are missing. My code can even handle the .. input case.
I know that APL is difficult to read, and since people enjoy understanding how a piece of code actually works, here are some explanation. Basically, I compute the final denominator in the variable D and the final numerator in the variable N.
APL is parsed from right to left.
- First, the string is stored in variable I (
I←).
- Then it is mapped to a vector of booleans indicating where a dot is, and this vector is called P (
P←'.'=). For instance '1.2.3' will be mapped to 0 1 0 1 0.
- This vector is digits in base 10 (
10⊥); now '1.2.3' is 1010.
- Then 1 is substracted from this number (either with
1-⍨ or with ¯1+, here I chose the second). Now '1.2.3' is 1009.
- Then this number is converted to a string (
⍕), two initial digits are removed (2↓), which makes 09 from our initial '1.2.3' example; the string is reversed (⌽).
- Here, as a special case, I add an initial 0 character in front of the string; it makes me sad to use the four characters
'0', but I did it for avoiding an error when the second and thirds fields are both empty. The string is converted back to a number (⍎) and it is stored in D, which is the denominator except when both last fields are empty, because in such case D is equal to 0.
- The
D←D+0= piece of code set D to 1 if it is currently null, and now D contains the denominator (before GCD division however).
- This denominator is multiplied (
×) with the content of the initial string I up to the second dot with (⍎'0',I/⍨2>+\P) which starts from P again (0 1 0 1 0 in my example), adds the successive numbers by cumulating them (which makes 0 1 1 2 2 in my example), check which values are smaller than 2 (making the boolean vector 1 1 1 0 0), and taking corresponding characters in I; another 0 is added in front of the string for preventing another trap (if the two initial fields are empty) and the whole is converted to a number.
- The last part of the input string is added to the previous product with
(⍎'0',1↓I/⍨2=+\P), which takes P again, adds by cumulating again, check which values are equal to 2 (see previous explanation), takes the characers, removes the first one which is a dot, adds a preventing initial 0 character and converts to a number.
- This product followed with a sum is stored in N which is the numerator.
- Finally the GCD is computed with D∨N and both numbers are divided by this GCD.
edit: Here is a fix for 73 characters:
(N,D)÷D∨N←(⍎'0',1↓P/I)+(⍎'0',I/⍨~P←2=+\P)×D←D+0=D←⍎'0',⌽2↓⍕¯1+10⊥P←'.'=I←
The idea of this hack is computing first the case where cumulative addition has values equal to 2, storing them for later and inverting this bitwise mask for getting the first case; thus computing the next case needs less characters.
edit: Here is another fix for 69 characters:
(N,D)÷D∨N←(⍎'0',1↓P/I)+(⍎'0',I/⍨~P←2=+\P)×D←⍎'1⌈0',⌽2↓⍕¯1+10⊥P←'.'=I←
The idea of this hack is to embed the most complicated special case as APL code in the string to be evaluated (at string to number conversion stage).
edit: Here is another fix for 68 characters:
(N,D)÷D∨N←(⍎'0',1↓P/I)+(⍎'0',I/⍨~P←2=+\P)×D←⍎'1⌈0',⌽3↓⍕1-10⊥P←'.'=I←
The idea of this hack is to replace adding -1 to the value for substracting 1 to that value by the operation substracting that value to 1 then remove later one character more at the beginning (which will be the minus sign).
edit: Cosmetic change:
(N,D)÷D∨N←(⍎'0',1↓P/I)+(⍎'0',I/⍨~P←2=+\P)×D←1⌈⍎'0',⌽3↓⍕1-10⊥P←'.'=I←
No improvement in size, but more satisfied to get the maximum function out of the code to be evaluated.


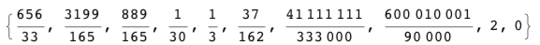
1Is it necessary to simplify the fraction? Or is it reasonable to leave it in an unsimplified form (eg:
9/99)? – Justin – 2014-01-07T18:57:33.0673
(in lowest terms)i.e. the fraction must be simplified. – Joe Z. – 2014-01-07T18:58:28.2572Am I allowed to output
13instead of13/1? – mniip – 2014-03-14T13:56:07.740@mniip: No, it has to be
13/1. – Joe Z. – 2014-03-14T18:46:21.503@JoeZ. Ok, I edited my answer – mniip – 2014-03-14T19:27:26.963
What range of numbers does this have to handle? Is it OK to assume the parts of the input are less than 2^31 or something like that? – Omar – 2014-03-14T20:03:57.207
4Be sure to handle this input
1.9999...and output2/1– Thomas Eding – 2014-03-14T20:08:48.987I think this piece of J code is much more powerful than what is asked since it doesn't require the second dot as a hint; may I post it
(((0:`(%@$:)@.(<&100))@%@-+])x:@<.) 5.3878787878787(35 characters)? – Thomas Baruchel – 2014-03-15T21:23:04.997@ברוכאל How does it handle something like
0.01020408163265306122448979590102040816326530...which looks like1/98but actually isn't? – Joe Z. – 2014-03-15T21:43:45.523@Joe Z. It actually will tell 1/98. – Thomas Baruchel – 2014-03-15T21:49:33.847
One more question: is the "slash" symbol a requirement? Could a space be OK as long as it follows other conventions (even the "13/1" convention as "13 1")? I ask because the slash is only a symbol for representing the fraction; anyway the Mathematica solution doesn't use the slash since it outputs a graphical representation of the fraction? – Thomas Baruchel – 2014-03-16T07:27:26.663
@ברוכאל If it tells
1/98for my input of0..0102040816326530612244897959, then your solution is invalid, because the correct answer is just102040816326530612244897959/9999999999999999999999999999. – Joe Z. – 2014-03-17T03:23:56.963Also, the slash symbol is only a requirement if your solution outputs plain text. In the case of the Mathematica solution, the fraction line serves the same purpose. – Joe Z. – 2014-03-17T03:24:28.290
@Joe Z. Thank you for all your answers; I finally made up a 68-characters APL code; separator is a space because the return value is a 'tuple' numerator+denominator; is it OK? All rules have been strictly followed. – Thomas Baruchel – 2014-03-17T05:57:31.843
I think that should be okay. – Joe Z. – 2014-03-17T13:57:24.453
3@ThomasEding
1.9999.is19999/10000, to get2/1you need1..9, isn't it? – Qwertiy – 2014-12-05T08:07:38.863