Drawing the Peano curve

Question

Introduction

In geometry, the Peano curve is the first example of a space-filling curve to be discovered, by Giuseppe Peano in 1890. Peano's curve is a surjective, continuous function from the unit interval onto the unit square, however it is not injective. Peano was motivated by an earlier result of Georg Cantor that these two sets have the same cardinality. Because of this example, some authors use the phrase "Peano curve" to refer more generally to any space-filling curve.

Challenge

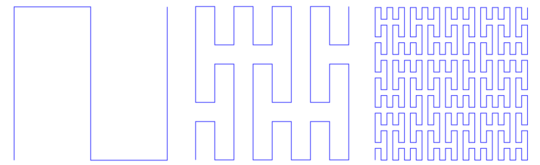
The program takes an input which is an integer n, and outputs a drawing representing the nth iteration of the Peano curve, starting from the sideways 2 shown in the leftmost part of this image:

Input

An integer n giving the iteration number of the Peano curve. Optional, additional input is described in the bonuses section.

Output

A drawing of the nth iteration of the Peano curve. The drawing can be both ASCII art or a "real" drawing, whichever is easiest or shortest.

Rules

• The input and output can be given in any convenient format (choose the most appropriate format for your language/solution).
• No need to handle negative values or invalid input
• Either a full program or a function are acceptable.
• If possible, please include a link to an online testing environment so other people can try out your code!
• Standard loopholes are forbidden.
• This is code-golf so all usual golfing rules apply, and the shortest code (in bytes) wins.

Bonuses

Since this shouldn't be a walk in the park (at least in most languages I can think of), bonus points are awarded for the following:

• -100 bytes if your code generates a gif of the construction of the Peano curves up to n.
• -100 bytes if your code draws a space-filling curve for any rectangular shape (the Peano curve only works for squares, obviously). You can assume that the input then takes on the form n l w where n has the same meaning as before (the number of the iteration), but where l and w become the length and width of the rectangle in which to draw the curve. If l == w, this becomes the regular Peano curve.

Negative scores are allowed (but are they possible...).

Edit

Please include the output of your program in the solution for n == 3 (l == w == 1).

Answer 1

Mathematica, score 60 - 100 - 100 = -140

Graphics[PeanoCurve@a~Reverse~3~Scale~#2]~Animate~{a,1,#,1}&

Pure function. Takes n and {l, w} (width and height) as input, and gives an animated graphic as output. It first creates a nth order Peano curve with PeanoCurve. Since the l = w case still needs to create a Peano curve, we flip the expression at level 3, similar to DavidC's answer; for l ≠ w, we just Scale the curve to the rectangle. This curve will still be space-filling, satisfying the second bonus. For the first bonus, we just Animate it over all sizes. Note that OP suggested that this was sufficiently different from DavidC's to warrant its own answer. The result for n = 3, l = w = 1 is as follows:

Answer 2

GFA Basic 3.51 (Atari ST), 156 134 124 bytes

A manually edited listing in .LST format. All lines end with CR, including the last one.

PRO f(n)
DR "MA0,199"
p(n,90)
RET
PRO p(n,a)
I n
n=n-.5
DR "RT",a
p(n,-a)
DR "FD4"
p(n,a)
DR "FD4"
p(n,-a)
DR "LT",a
EN
RET

Expanded and commented

PROCEDURE f(n)      ! main procedure, taking the number 'n' of iterations
  DRAW "MA0,199"    !   move the pen to absolute position (0, 199)
  p(n,90)           !   initial call to 'p' with 'a' = +90
RETURN              ! end of procedure
PROCEDURE p(n,a)    ! recursive procedure taking 'n' and the angle 'a'
  IF n              !   if 'n' is not equal to 0:
    n=n-0.5         !     subtract 0.5 from 'n'
    DRAW "RT",a     !     right turn of 'a' degrees
    p(n,-a)         !     recursive call with '-a'
    DRAW "FD4"      !     move the pen 4 pixels forward
    p(n,a)          !     recursive call with 'a'
    DRAW "FD4"      !     move the pen 4 pixels forward
    p(n,-a)         !     recursive call with '-a'
    DRAW "LT",a     !     left turn of 'a' degrees
  ENDIF             !   end
RETURN              ! end of procedure

Example output

Answer 3

Perl 6, 117 bytes

{map ->\y{|map {(((++$+y)%2+$++)%3**(y+$^v,*/3...*%3)??$^s[$++%2]!!'│')xx$_*3},<┌ ┐>,$_,<└ ┘>,1},^$_}o*R**3

Try it online!

0-indexed. Returns a 2D array of Unicode characters. The basic idea is that for lower rows, the expression

(x + (x+y)%2) % (3 ** trailing_zeros_in_base3(3*(y+1)))

yields the pattern

|....||....||....||....||..  % 3
..||....||....||....||....|  % 3
|................||........  % 9
..||....||....||....||....|  % 3
|....||....||....||....||..  % 3
........||................|  % 9
|....||....||....||....||..  % 3
..||....||....||....||....|  % 3
|..........................  % 27

For upper rows, the expression is

(x + (x+y+1)%2) % (3 ** trailing_zeros_in_base3(3*(y+3**n)))

Explanation

{ ... }o*R**3  # Feed $_ = 3^n into block

map ->\y{ ... },^$_  # Map y = 0..3^n-1

|map { ... },<┌ ┐>,$_,<└ ┘>,1  # Map pairs (('┌','┐'),3^n) for upper rows
                               # and (('└','┘'),1) for lower rows.
                               # Block takes items as s and v

( ... )xx$_*3  # Evaluate 3^(n+1) times, returning a list

 (++$+y)%2  # (x+y+1)%2 for upper rows, (x+y)%2 for lower rows
(         +$++)  # Add x
                   (y+$^v,*/3...*%3)  # Count trailing zeros of 3*(y+v) in base 3
                3**  # nth power of 3
               %  # Modulo
??$^s[$++%2]  # If there's a remainder yield chars in s alternately
!!'│'         # otherwise yield '│'

Answer 4

K (ngn/k), 37 27 26 bytes

{+y,(|'y:x,,~>+x),x}/1,&2*

Try it online!

returns a boolean matrix

|'y is syntax specific to ngn/k. other dialects require a : to make an each-ed verb monadic: |:'y

Answer 5

Wolfram Language 83 36 bytes, (possibly -48 bytes with bonus)

As of version 11.1, PeanoCurve is a built-in.

My original, clumsy submission wasted many bytes on GeometricTransformation and ReflectionTransform.

This much reduced version was suggested by alephalpha. Reverse was required to orient the output properly.

Graphics[Reverse/@#&/@PeanoCurve@#]&

Example 36 bytes

Graphics[Reverse/@#&/@PeanoCurve@#]&[3]

---

Bonus

If this qualifies for the 100 pt bonus, it weighs in at 52 - 100 = -48 The code [5] was not counted, only the pure function.

Table[Graphics[Reverse/@#&/@PeanoCurve@#]&@k{k,#}&[5]

Answer 6

HTML+SVG+JS, 224 213 bytes

The output is mirrored horizontally.

n=>document.write(`<svg width=${w=3**n*9} height=${w}><path d="M1 ${(p=(n,z)=>n--&&(p(n,-z,a(a(p(n,-z,d+=z)),p(n,z))),d-=z))(n*2,r=d=x=y=1,a=_=>r+=`L${x+=~-(d&=3)%2*9} ${y+=(2-d)%2*9}`)&&r}"fill=#fff stroke=red>`)

Try it online! (prints the HTML)

(
n=>document.write(`<svg width=${w=3**n*9} height=${w}><path d="M1 ${(p=(n,z)=>n--&&(p(n,-z,a(a(p(n,-z,d+=z)),p(n,z))),d-=z))(n*2,r=d=x=y=1,a=_=>r+=`L${x+=~-(d&=3)%2*9} ${y+=(2-d)%2*9}`)&&r}"fill=#fff stroke=red>`)
)(3)

Answer 7

BBC BASIC, 142 ASCII characters (130 bytes tokenised)

Download interpreter at http://www.bbcbasic.co.uk/bbcwin/download.html

I.m:q=FNh(m,8,8,0)END
DEFFNh(n,x,y,i)
IFn F.i=0TO8q=FNh(n-1,x-i MOD3MOD2*2*x,y-i DIV3MOD2*2*y,i)DRAWBY(1AND36/2^i)*x,y*(12653/3^i MOD3-1)N.
=0

Answer 8

Logo, 89 bytes

to p:n:a
if:n>0[rt:a
p:n-1 0-:a
fw 5
p:n-1:a
fw 5
p:n-1 0-:a
lt:a]end
to f:n
p:n*2 90
end

Port of @Arnauld's Atari BASIC answer. To use, do something like this:

reset
f 3

Answer 9

Stax, 19 bytes

∩▐j>♣←╙~◘∩╗╢\a╘─Ràô

Run and debug it

Output for 3:

███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ █
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
█         █ █         █ █         █ █         █ █    
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
    █ █         █ █         █ █         █ █         █
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
█ ███ ███ ███ ███ ███ ███ ███ ███ █ █ ███ ███ ███ ███
█                                 █ █                
█ ███ ███ ███ ███ ███ ███ ███ ███ █ █ ███ ███ ███ ███
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
    █ █         █ █         █ █         █ █         █
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
█         █ █         █ █         █ █         █ █    
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
███ ███ ███ ███ █ █ ███ ███ ███ ███ ███ ███ ███ ███ █
                █ █                                 █
███ ███ ███ ███ █ █ ███ ███ ███ ███ ███ ███ ███ ███ █
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
█         █ █         █ █         █ █         █ █    
█ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
    █ █         █ █         █ █         █ █         █
███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █ █ ███ ███ █
█ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███ ███